La prouvabilité formelle

Le mécanisme permet de donner une motivation ou même une justification plus directe et n'usant pas de la moindre goutte de psychologie populaire pour la formule C. En effet, si on interprète $p$ par Bew$(p\; )$ où $p$ désigne le nombre de Gödel d'une description formelle de la proposition $p$ et où ``Bew" (Bew$eisbar$) désigne le prédicat de prouvabilité de Gödel, alors, la formule C correspond au second théorème d'incomplétude de Gödel [Gödel, 1931].
On peut justifier, comme de nombreux auteurs, que le théorème de Gödel s'applique (au moins) aux machines universelles ``suffisamment riches" (capables de prouver leur propre $\Sigma$₁-complétude). Et on peut conclure, avec le mécanisme, ou à partir de réflexions concernant les fondements des mathématiques comme celles de Webb et de Myhill [Webb, 1980, Myhill, 1952], que le (second) théorème de Gödel s'applique à nous. Il est en quelque sorte le premier théorème de ``psychologie exacte". Il affirme, en terme de machine, qu'aucune machine (potentiellement) universelle, consistante et ayant les ``facultés introspectives" suffisantes pour prouver sa ``propre" $\Sigma$<sub>1</sub>-complétude, n'est capable de prouver sa ``propre" consistance. Je qualifierai une telle machine de löbienne en référence à l'article de Löb [Löb, 1955]. Voir plus bas.
Le terme ``propre" est mis entre guillemets car l'autoréférence gödélienne, étant complètement arithmétisable, ne permet pas de distinguer une ``machine originale" d'une copie. Il s'agit donc d'une autoréférence à la troisième personne. Avec la prouvabilité formelle, la machine démontre des propositions la concernant, mais concernant tout autant une machine quelconque parmi ses doppelgängers. Gödel (1933) avait déjà constaté qu'il n'était pas possible d'utiliser la prouvabilité formelle pour formaliser la connaissance qui par nature est de la première personne. En effet, il faudrait qu'une machine consistante puisse communiquer les équivalents arithmétiques des formules $A\; \to A$ (généralement admises pour la connaissance), mais cette communication contredirait le second théorème d'incomplétude. Cela découle directement des équivalences classi$ques\; :$

Il n'en demeure pas moins qu'apparaît ici une phénoménologie naturelle de la communication (correcte et à la troisième personne) par une machine au sujet d'une version d'elle-même.
A partir de ce moment, il n'est pas possible de ne pas tenir compte d'une histoire (essentiellement hollandaise, italienne, soviétique, américaine) où, afin d'être court, je mentionne deux événements charnières:

• La réponse de Löb au problème de Henkin: que peut-on dire d'une formule arithmétique énonçant sa propre prouvabili$té\; ?Löb\; démontre\; qu\text{'}une\; telle\; formule\; est\; (paradoxalement)\; nécessairement\; vraie\; et\; prouvable\; [Löb,\; 1955].$
• Les deux théorèmes de complétude de Solovay [Solovay, 1976].
  1. Solovay découvre que la formule (dite de Löb, c'est la version modale de la formalisation arithmétique du théorème de Löb)

     

     permet, accompagnée de la traditionnelle formule de Kripke

     

     et des règles d'inférence du modus ponens et de la nécessitation d'axiomatiser complètement la part prouvable par la machine de la logique de la prouvabilité formelle (arithmétisable) de la machine (précisément la logique modale ou le carré modélise le $Beweisbar$ de Gödel). G désigne (souvent) la théorie obtenue.
  2. Dans le même article, Solovay démontre que si on adjoint aux théorèmes de G les formules de réflexion , et que l'on ferme le système exclusivement par la règle du modus ponens (en abandonnant donc la règle de nécessitation) on obtient une théorie (souvent appelée G$*$) qui axiomatise complètement la part vraie (et non pas simplement la part prouvable par la machine) de la logique de la prouvabilité formelle (arithmétisable) de la machine. En particulier G$*$ prouve . En outre G et G$*$ sont décidables.

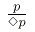G$*\; \backslash \; G,\; la\; part\; vraie\; mais\; incommunicable\; (à\; la\; troisième\; personne)\; de\; la\; machine\; Löbienne\; constitue\; une\; curieuse\; logique\; décidable\; et\; fermée,\; comme\; G$ *$,\; pour\; le\; modus\; ponens\; et\; la\; ``possibilisation"$ (voir plus loin). Avec le computationnalisme, G$*\; \backslash \; G\; axiomatise\; en\; quelque\; sorte\; un\; réservoir\; de\; propositions\; seulement\; inférables\; et\; jamais\; communicables.$ De façon précise, voici une présentation de la logique G:

Définition $R$ désignant une relation d'accessibilité (voir 1.2), une échelle infinie est une suite de mondes $a$₀, a₁, a₂, a₃, ... tel que $a$₀Ra₁Ra₂Ra₃R...
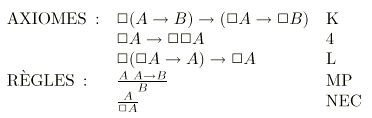
Définition R est bien chapeautée ssi il n'existe pas d'échelles infinies.
On peut démontrer que 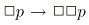$(W,R)$ respecte les formules et 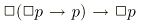ssi R est transitive et bien chapeautée. En fait on a le résultat de complétude suivant

De même, voici G$*$

G$*$ n'est pas fermé pour la règle de nécessitation, ni même pour la règle de monotonie. Il n'admet donc ni sémantique de Kripke, ni sémantique de Scott-Montague. Boolos, à partir d'une idée de Solovay, a néanmoins trouvé une intéressante sémantique de Kripke variable pour G* [Boolos, 1980c, Solovay, 1976], voir aussi [Boolos, 1980a, Marchal, 1995].
Pour énoncer de façon rigoureuse les résultats de complétude arithmétique de Solovay, il faut préciser la façon dont les formules modales sont interprétées arithmétiquement. A cette fin on définit une ``réalisation" $F$ qui associe à chaque variable propositionnelle $p$<sub>i</sub> un énoncé arithmétique, ou dans notre contexte un énoncé dans le langage de la machine löbienne M. L'interprétation arithmétique des formules se définit alors par induction sur la complexité des formules. Pour une formule modale le carré est interprété par le Bew arithmétique de Gödel. J'appelle ``morphisme de Magari-Boolos" cette interprétation arithmétique de la logique modale [Magari, 1975].

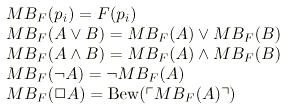
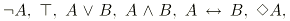Les formules , sont considérées, ici, comme des abréviations de 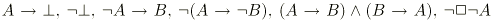respectivement. Le premier théorème de complétude de Solovay devient:

Théorème 7

et le second devient:

Théorème 8

Autrement dit, si la traduction d'une formule modale est vraie (arithmétiquement, ou dans le langage de $M$, etc.) alors G* la démontre.
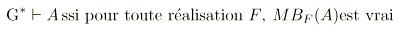
Solovay a montré que G est décidable. De même il a montré en introduisant une transformation modale particulièrement intéressante que la décidabilité de G$*$ se ramène à celle de G:

Proposition 9

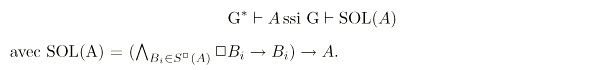
où $S$(A) désigne l'ensemble des formules $B$_i avec B_i sous-formules de $A$.
De cette façon la formule SOL($A$) permet de considérer un philosophe mécaniste assez ``prudent". Pour choisir un niveau de description, il exige non pas une preuve (impossible) de l'adéquation du niveau, (c'est-à-dire une preuve qu'il ne va jamais finir (mourir) dans un monde accessible avec le télétransport), mais une preuve de l'adéquation du niveau pour chacune de ses parties finies, ainsi qu'une preuve que la conjonction des ``réflexions" de ces parties finies entraîne sa survie. Dans ce cas il utilise le télétransport. Il reste imprudent car il ne sait toujours pas si le niveau du mécanisme choisi est adéquat, et en particulier si G$*$ s'applique à lui-même ``vu comme formule arithmétique" relativement à ce niveau. Mais, si le mécanisme est correct et si son choix est adéquat, il aura prouvé le plus qu'il est possible, par les deux théorèmes de Solovay, de prouver, pour un mécaniste.

G^* \ G constitue un espace des solutions à notre équation 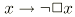. Justifier sa survie au télétransport est analogue à la preuve de la consistance d'une de ses extensions. Notons (avec la sémantique de Kripke) que l'axiome modale 4 est un théorème de G, ce qui pose des problèmes pour l'utilisation directe de G pour la mesure de l'indéterminisme (le ``calcul des probabilités"). En effet la formule 4 entraîne la transitivité pour la relation d'accessibilité, et la sélection concerne les extensions immédiates. Je suggèrerai dans la section suivante une variante d'une idée de Théétète qui entraîne la disparition de 4 et la disparition de la fermeture pour la nécessitation.

G^* \ G est-il une logique ? Tenter de définir ce qu'est une logique nous entraînerait trop loin. Je me contente de deux remarques:

1. Aucune tautologie classique (ni intuitioniste^foot donc) n'est ``démontrable" par (c'est-à-dire n'appartient à) G$*\; \backslash$ G, puisque G démontre les tautologies classiques.
2. G^* \ G est, quand même, fermé pour le modus ponens (MP). En effet, si 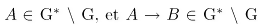, alors 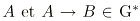, et donc 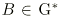puisque G^* est fermé pour MP. D'autre part, 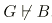,sinon G prouverait A -> B. En effet avec MP et le schéma tautologique (classique et intuitioniste) 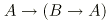, on dérive la règle 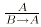. Donc .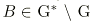