Modular automatic design of collective behaviors for robots endowed with local communication capabilities

Ken Hasselmann and Mauro Birattari (April 2020)

Decision

Note on EvoComX and Gianduja{X,EX}

A letter X in the name of a method indicates that the information on the direction from which messages arrive is disregarded (the letter X is the mnemonic for excluded).
We included in this supplementary material the X-versions of all methods to appraise the impact on performance of the information provided by $V_b$. We wish to see whether it is more the advantage of reducing the search space or the disadvantage of discarding the directional information provided by $V_b$.

EvoComX is an automatic design method derived from EvoCom. The only difference between EvoComX and EvoCom is that EvoComX disregards the $V_b$ vector. The network has only 26 input nodes, instead of the 30 of EvoCom. The four missing nodes are the scalar projection of $V_b$ on the four units vectors.

GiandujaX is derived from Gianduja. The only difference is that GiandujaX disregards the information provided by $V_b$. This implies that GiandujaX does not use two behaviors of Gianduja: attraction-to-message and repulsion-from-message. In all other respects, GiandujaX is identical to Gianduja.

GiandujaEX presents the characteristics of GiandujaX and GiandujaE; robots do not use directional information provided by $V_b$, as in GiandujaX; and implement the transition conditions of GiandujaE. In all other respects, GiandujaEX is identical to Gianduja.

Statistical data

The statistical data of all runs is available for download.

Videos

You can find below three videos per mission that illustrates the real robot behavior of the 3 methods tested in reality. All the other videos ar also available for download below.

Decision

The videos of all experimental runs are available for download.

You can find below the robot behavior of all 7 methods tested in pseudo-reality

Examples of probabilistic finite-state machines

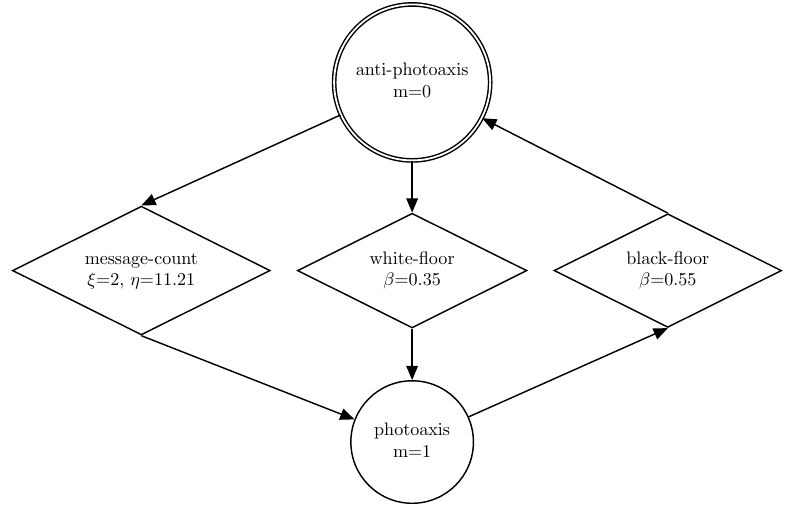
Examples of probabilistic finite-state machines produced by Gianduja: In all states, $m$ is the broadcast parameter. For exploration, $\tau$ is the random turns parameter. For attraction, $\alpha$ is the attraction factor. For (inverted)-neighbors-count and (inverted)-message-count, $\xi$ and $\eta$ are parameters used to compute the transition probability. In all other conditions, $\beta$ is the transition probability. For further details on the parameters, we refer the reader to the Design Method section of the paper

Decision

The controllers of all experimental runs are available for download.