The
Origin of Physical Laws and Sensations
Bruno Marchal, IRIDIA, Université de Bruxelles
Résumé : I will first present a non constructive
argument showing that the mechanist hypothesis in cognitive science gives
enough constraints to decide what a "physical reality" can possibly
consist in. Then I will explain how computer science, together with logic,
makes it possible to extract a constructive version of the argument by
interviewing a Modest or Löbian Universal Machine. Reversing von Neumann probabilistic
interpretation of quantum logic on those provided by the Löbian Machine gives a
testable explanation of how both communicable physical laws and incommunicable physical knowledge, i.e.
sensations, arise from number theoretical relations.
Acknowledgment Thanks to my friends, my IRIDIA colleagues and
my correspondents of the Everything-List and of the Fabric-of-Reality-List for
helpful and encouraging discussions. I take full responsibility for any
possible error or awkwardness. Thanks to Brenda Langedijk and Walter Belgers
for the invitation at SANE 2004.
Introduction
A lot of literature exists arguing for or
against the mechanist hypothesis, roughly speaking the idea that we are
machines, and this well before and after Descartes, Hobbes and their followers
redeemed it in the so-called modern (recent) tradition.
It is not the purpose of this paper to argue for neither against
mechanism. I propose instead to consider it as a working hypothesis, and to search its logical consequences. It will be
easier to consider a stronger digital
version of it, if only in order to get precise definitions crossing different
scientific disciplines. Proceeding in this way will eventually leads us toward
“pure” scientific questions, in the Popper testable sense, in particular under
the form of mathematical and physical problems. It is not entirely unreasonable
to expect a frank contradiction, in which case we would get a “refutation” of
digital mechanism, but we must be careful not to confuse a contradiction with
just some amount of weirdness[1].
Definition:
Classical Digital mechanism, or Classical Computationalism, or just
comp, is the conjunction of the following three sub-hypotheses:
1) The yes doctor hypothesis: It is the
assumption, in cognitive science, that it exists a level of description of my
parts (whatever I consider myself to be[2])
such that I would not be aware of any experiential change in the case where a
functionally correct digital substitution is done of my parts at that level. We
call that level the substitution level. More simply said it is the act of faith of those willing to say yes to their doctor for an artificial
brain or an artificial body graft made from some description at some level. We
will see such a level is unknowable. Note that some amount of folk or
“grand-mother psychology” has been implicitly used under the granting of the
notion of (self) awareness[3].
2) Church Thesis. A modern version is that all
digital universal machines are equivalent with respect to the class of
functions (from the natural numbers to the natural numbers) they can compute[4].
It can be shown that this entails such machines compute the same functions, but
also they can compute them in similar ways, i.e. following similar algorithm.
So, the thesis says, making abstraction of computation time, all digital
universal machine can simulate each other exactly (I will say emulate each other).
3) Arithmetical Realism (AR). This is the assumption that
arithmetical proposition, like “1+1=2,” or Goldbach conjecture, or the
inexistence of a bigger prime, or the statement that some digital machine will
stop, or any Boolean formula bearing on numbers, are true independently of me,
you, humanity, the physical universe (if that exists), etc. It is a version of
Platonism limited at least to arithmetical truth. It should not be confused
with the much stronger Pythagorean form of
To state the main results, it is helpful to
give in advance the following definitions, although more precise formulations
will be given naturally through the argumentation itself.
Definition Fundamental Physics: I define it by the
correct-by-definition discourse about observable and verifiable anticipation of
possible relatively evolving quantities and/or qualities.
We have tremendous empirical evidences that quantum mechanics is part
of such a physics. [See Cabello quasi exhaustive and well ordered bibliography
in the archive at
Definition Fundamental Machine Psychology: I define
it by the correct-by-definition discourse that machines could have about
themselves or about other machines. This will include in particular computer
science, but also sets of propositions that some machine could correctly
asserts about itself (named self-referentially correct discourses).
There is nothing normative in the
use of the word “correct”: if we ever knew that the reason the moon appears
in the sky is that 667 little angels are pushing it there, then that would be the correct-by-definition
explanation. We don’t need to elaborate: eventually the word “correct” will
just mean arithmetically true. This should be made clear through the reasoning
which will follow.
The paper is divided into two parts:
Part 1
presents an informal but (hopefully) rigorous argument or proof, named the
Universal Dovetailer Argument (UDA), in the form of a sequence of eight thought
experiences[5],
showing that it follows from comp that fundamental physics is necessarily
reducible to fundamental psychology.
Note that with comp, fundamental psychology is itself easily shown to be
embeddable in number theory[6].
Part 2,
thanks to the many discoveries of Gödel, Church, Turing, Post, Markov and many
others (mainly the studies of Brouwer, Heyting, Löb, Grzegorczyk, Boolos,
Goldblatt, Kuznetsov, Muravitski, Solovay, Visser) in the study of the self and
in Arithmetical Self-Reference, will explain how to interview a
Self-Referentially Correct Universal Machine (SRC Machine) on the UDA’s
conclusion to derive some comp logic of physical propositions. Then we will
compare that logic with the empirical logic of physical propositions which have
been inferred from observations. This will show that comp is testable and even
that some test does already confirm it (and this does not mean that it proves
it, of course). Before addressing the proof of the psychology/physics reversal
and its mathematical confirmation, let me warn the sensible person that both
can produce some amount of metaphysical vertigo[7].
I. The Universal
Dovetailer Argument shows why comp necessarily forces a reversal between
physics and machine psychology
Here is
presented the argument showing that if we take seriously enough the
computationalist hypothesis in the cognitive science then physics is reducible
to machine psychology. The proof is divided into 8 steps. Each step is numbered
and accompanied by a drawing featuring the principal idea of the step.
1) Comp makes possible (only in principle but that is all we need),
the use of classical[8]
teleportation. You are read and cut, with the usual computer practice meaning,
at

In the
figure the teleported individual is represented by a black box. Its
annihilation is represented by a white box appearing at the left of the arrow.
The reconstitution is represented by a white box at the right of the arrow. If
we identify an individual with its (hopefully consistent) set of beliefs, the
experience adds only a new belief (I did arrive in
2) The step and figure 1 are just a restatement
of the comp hypothesis. To proceed we need to introduce a key distinction
between the notions of first person point of view and third person point of
view. It will be enough, in the argument itself, to define them by the
propositional content of personal diaries. The third person point of view is
the content of a description of the experiment by an external observer which
does not participate in the teleportation. The first person point of view is
the content of the diary taken by the user of teleportation device. He is
supposed to take it with him, so that the personal diary will be itself
destroyed and reconstituted. To ease the reasoning, we neglect at first reading and pasting time, as we neglect the time travel of the descriptive
information. In this simple teleportation experiment/experience there is no
difference between the first and third person discourse, giving that both
diaries will describe someone going from
Giving that
we assume comp, the “experiencer” has no ability, if deprived of any external
clues (the reconstitution box has no window, etc.), to know anything about that
delay. His diary will not and cannot mention it, so that the first person
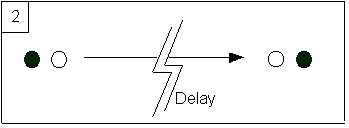
discourse is the same as in the preceding experiment. Contrariwise, the diary
of the external observer will mention that very long delay. At step two the
first and third person discourses are no more the same.
3) The third step is admittedly intriguing; its
consequences are no less. The description encoded at
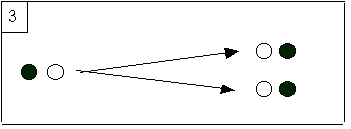
So after the experiment each “first
person” will feel to be at one place. To be at both places will never be a
realisable consistent belief from the first person point of view. Giving the
built-in symmetry of this experiment, if asked before the experiment about his
personal future location, the experiencer must confess he cannot predict with
certainty the personal outcome of the experiment. He is confronted to an
unavoidable uncertainty. This is remarkable because from a third person point
of view the experiment is completely deterministic, and indeed the mechanist
doctrine is defended most of the time by advocates of determinism. But we see
here that mechanism, by being indeed completely 3-deterministic, entails a
strong form of indeterminacy[10],
bearing on the possible consistent extensions, when they are observed by the
first person, as both diaries can witness. This is what I call the first person
comp indeterminacy, or just
1-indeterminacy. Giving that
4) The fourth step shows that the
invoked symmetry and simultaneity was a red erring sort of justification. For this purpose, it is enough to introduce
in the preceding setup a delay of reconstitution in one of the bifurcating
branches. Then we can use the fact, established at the second step, that a
person, from his inner first personal point of view cannot be aware of the
delay to understand that the introduction of asymmetric delays will not change
the first person perspective. Although a precise measure of the first person
uncertainty has not been (and never will be) defined in a precise way, the key
point is that such a measure does not change for such delays. In particular, if ever we did decide to attribute a probability of ½ on the consistent
extensions at step 3, then we must
also attribute a probability of ½ in the asymmetrical duplication, and that’s
the point we wanted to show.
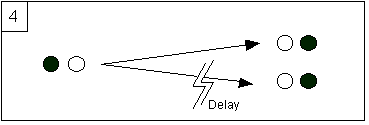
5) Until now, the one we could
call conventionally “the original” has always been annihilated at

The absence
of the white blob at the left means there is no annihilation at the starting
point. We can also consider there is a natural implicit delay on the arrow. It
is a consequence of the preceding steps that if the probability is ½ at step 3
(and thus also at step 4), it must be ½ at step 5. The reason is that this
setup can be reconsidered equivalently as a duplication-teleportation (like in
step 4) from
6) The sixth step is akin to the oldest
metaphysical argument. It is also the most perennial and universal, it is
discussed in old Hindouist, Buddhist, Taoist, Islamic, Jewish and Christian texts.
It plays a role in Plato’s Theaetetus, and Descartes’ Meditations, and many
others. In his comp form, it is exploited in many Science Fiction Novels; like Simulacron III by Daniel Galouye, or in
movies, like The Matrix. It is the dream argument, and it shows mainly that
we can always erroneously take a mere belief for knowledge. We will see how the
sound universal machine will reflect that insight in its self-referentially
correct discourses, but at this stage, all we need amounts only to the following
consequence of comp: all the preceding steps can be done again with the
reconstitution being “virtual,” i.e. emulated by a universal machine, instead of “real” and this without any
possible change in the experience of the first person for some arbitrary finite
time related to the accuracy of the rendering of the environments (like
Washington and Moscow for example). All you need is to simulate the right
interface, which is Turing emulable, by definition of comp, and then some
approximation of the environment will succeed, the finer in descriptive
details, the longer in time. Comp makes it possible to replace dreams by video
games in the old dream argument in the sense that a first person cannot
distinguish “reality” from an emulation of it when done at a level lower than
its substitution level.

In figure
6, the box represents a (finite) computing machinery. What matter here, is that
whatever measure of the comp 1-indeterminacy we choose, that measure will not
change in the case where the reconstitution are virtual. Even if the simulation
does not last, each first person will take any personal reconstitution as
confirming its anticipation, i.e. its bets on its consistent extensions. The
probability calculus is again invariant for such a change. This follows
directly from our earlier comp assumption that a correct substitution level
exists, and that we are Turing emulable.
7) The seventh step introduces the Universal
Dovetailer (UD). Let N denotes the set of natural numbers. A function from N to
N is said to be total if it is defined on all natural numbers. A function is
said to be computable iff there is a programme FORTRAN which computes it[12].
Church thesis (CT) makes the particular choice of FORTRAN irrelevant. CT claims
that all computable functions, total or not, are computed by algorithm
expressible in FORTRAN. In particular all total computable functions are
computed by such FORTRAN program.
Is there a language, T-Fortran say,
which would be capable of defining all and only
all the total computable functions? T-Fortran language, by some
well-defined grammatical restrictions, would make any algorithms written in it
computing only total functions. The
answer is “no.” For, would it be the case, we could enumerate the T-Fortran
programs by lexicographical order: P1, P2, P3
…, and the following function g defined
on n by Pn(n)+1, would be computable, but not T-Fortran computable.
Indeed, there would exist a T-Fortran programme Pk computing it,
then Pk(k) = Pk(k) + 1, and that’s absurd giving that Pk(n)
is a well defined number for each n (because the function are total). So, with
Church thesis, the set of programs computing total functions is necessarily a
proper subset of the set of programs computing functions written in FORTRAN.
FORTRAN itself is vaccinated against the preceding diagonal “attack”. Indeed,
although we can enumerate all FORTRAN programs (and this can be done
mechanically), and although the resulting diagonal function g can be programmed
in FORTRAN, and that it will on its code give again g(k) = g(k) + 1, we will
not get a contradiction, but only, in the computer science jargon, a crashing
of the computer, that is, the computation of g(k) will just run forever. And
this entails there is no complete and decidable theory capable of deciding from
a program description if it computes a total or a non total function, because
in that case we would be able to use that theory to mechanically filtered the
non total programs, and get, with CT, an enumeration of all and only all total
computable functions; but then we would obtain again the contradiction we got
above. This shows that the incompleteness of theories, with respect to truth,
is a direct consequence of CT. The absoluteness of computability, warranted by
CT, makes inescapable the relativity of theories. This again will be reflected
in our universal machine interview. Concerning the present step in the
reasoning, it explains why if we want build a universal machine, which is not
only able to emulate all machines, but which actually does the emulation of each machine, we will be obliged to dovetail
on each execution. We must generate all FORTRAN programs, P1, P2,
P3 …, and execute them by little pieces, coming back recurrently on
all programs. Let Pij(n) represents j steps of the
execution of the ith program Pi on input n. We must just
computes all those Pij(n), and that is easy because the
triple <i,j,n> are algorithmically enumerable. It can be seen as a manner
to emulate digital parallelism in a linear sequential way. This way avoids any
risk of never stopping on a possible infinite computation due to the necessary
existence of non stoppable programs, as we have just shown. Such a procedure is
called a dovetailing procedure, and I call a universal machine which dovetails
on all possible machine executions, a Universal Dovetailer (UD). Suppose now,
for the sake of the argument, that our concrete and “physical” universe is a
sufficiently robust expanding universe so that a “concrete” UD can run forever,
as illustrated in figure 7.
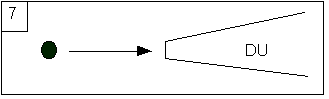
Then, it
follows from the six preceding steps that it will generate all possible Turing
machine states, infinitely often (why?), which (by comp) includes all your
virtual reconstitutions corresponding to (hopefully) consistent extensions of
yourself, in all possible (locally) emulable environments or computational
histories. And this, with comp, even in the case you consider that your
“generalised brain” (the “whatever” which is needed to be emulated by a digital
body/brain to survive) is the whole Milky Way galaxy. And we don’t need any
Science Fiction like devices to make this concrete[13],
if we make exception of the robust universe.
We are almost done. Indeed, let us try a simple
“physical experiment” like dropping a pen. With comp, when we are in the state
of going to drop the pen, we are in a Turing emulable state. Our more probable
consistent extension is undetermined by the 1-comp indeterminacy on all the
“reconstitution” of that similar states appearing in UD* (the infinite trace of
the UD). This follows from 6, and the invariance of the uncertainty measure,
notably for the arbitrary delay---including the null one, and the infinite set
of states appearing with a arbitrarily large delay in the running of the UD[14].
This gives a huge set. It can be argued that finite computations are of measure
null, and that the only way to a measure on the states will consist in finding
a measure on the set of maximally complete computational history going through
those states, with obviously a rather hard to define equivalence relation among
computations. Still, we can show that those (infinite) computations, as seen
from some third person description of UD*, correspond to maximally consistent
extensions of our (hopefully) actual consistent states. It is not necessary to
be more precise here, giving the non constructivism of the collection of those
consistent extensions, and the fact that we will make things utterly precise,
by directly interviewing a universal machine on those extensions, and this by
taking into account the 1/3 person point of view distinction. So, if we grant a
sufficiently robust universe, we are completely done: physics, as the “correct”
science for the concrete relative predictions must be given by some measure on
our consistent relative states. Physics is, in principle reduced to a measure
on the collection of computational histories, as seen from some first person
point of views. We can say that in principle, physics has been reduced to
computer fundamental psychology.
8) Yes, but what if we don’t grant a concrete robust physical universe? Up to this stage,
we can still escape the conclusion of the seven preceding reasoning steps, by
postulating that a “physical universe” really “exists” and is too little in the
sense of not being able to generate the entire UD*, nor any reasonable portions
of it, so that our usual physical predictions would be safe from any
interference with its UD-generated “little” computational histories. Such a move can be considered as being ad hoc and disgraceful. It can also be
quite weakened by some acceptation of some conceptual version of Ockham’s
Razor, and obviously that move is without purpose for those who are willing to
accept comp+ (in which case the UDA
just show the necessity of the detour in psychology, and the general shape of
physics as averages on consistent 1-histories).
But logically, there is still a place for both physicalism and comp, once we made that move. Actually the 8th
present step will explain that such a move is nevertheless without purpose.
This will make the notion of concrete and existing universe completely devoid
of any explicative power. It will follow that a much weaker and usual form of
Ockham’s razor can be used to conclude that not only physics has been epistemologically reduced to machine
psychology, but that “matter” has been ontologically
reduced to “mind” where mind is defined as the object study of fundamental
machine psychology. All that by assuming
comp, I insist. The reason is that comp forbids to associate inner experiences
with the physical processing related to the computations corresponding (with
comp) to those experiences. The physical “supervenience thesis” of the
materialist philosophers of mind cannot be maintained, and inner experiences
can only be associated with type of computation.
Instead of linking [the pain I feel] at
space-time (x,t) to [a machine state] at space-time (x,t), we are obliged to
associate [the pain I feel at space-time (x,t)] to a type or a sheaf of
computations (existing forever in the arithmetical Platonia which is accepted
as existing independently of our selves with arithmetical realism). That result
has been found independently by me and Tim Maudlin (Marchal 1988, Maudlin
1989). Maudlin’s argumentation provides more information[15].
The argument is less easy to apprehend than those of the preceding step and I
will only sketch the basic principle.
For any given precise running computation
associated to some inner experience, you can modify the device in such a way
that the amount of physical activity involved is arbitrarily low, and even null
for dreaming experience which has no inputs and no outputs. Now, having
suppressed that physical activity present in the running computation, the
machine will only be accidentally
correct. It will be correct only for that precise computation, with unchanged
environment. If it is changed a little
bit, it will make the machine running computation no more relatively correct.
But then, Maudlin ingenuously showed that counterfactual correctness can be recovered,
by adding non active devices which
will be triggered only if some (counterfactual) change would appear in the
environment. Now this shows that any inner experience can be associated with an
arbitrary low (even null) physical activity, and this in keeping counterfactual correctness. And that is absurd with the conjunction of
both comp and materialism.
So if we keep comp at this stage, we are forced
to relate the inner experience only to the type of computation involved. The
reason is that only those types are univocally related to all their possible
counterfactuals. This entails that, from
a first person point of view, not only the physical cannot be distinguished
from the virtual, but the virtual can no more be distinguished from the arithmetical[16].
Now DU is emulated platonistically by the verifiable propositions of
arithmetic. They are equivalent to sentences of the form “it exists n such that
P(n)” with P(n) decidable. Their truth entails their provability, and they are
known under the name of Sigma1 sentence.
If comp is correct, the appearance of physics
must be recovered from some point of views emerging from those propositions.
Indeed, taking into account the seven steps once more, we arrive at the
conclusion that the physical atomic (in the Boolean logician sense) invariant
proposition must be given by a probability measure on those propositions. A
physical certainty must be true in
all maximal extensions, true in at least one maximal extension (we will see
later why the second condition does not follow from the first) and accessible
by the UD, that is arithmetically verifiable.
Figure 8 illustrates our main conclusion, where the number 1 is put for
the so called Sigma1 sentences of arithmetic.
Conclusion: Physics is given by a measure on the
consistent computational histories,
or maximal consistent extensions as
seen from some first person point of view. Laws of physics, in particular,
should be inferable from the true verifiable “atomic sentences”. Those are the
verifiable arithmetical sentences. They should be true everywhere (= in all
comp histories), true somewhere (= true in at least one comp history), and
inferred from the DU-accessible “atomic” states[17].
II. The Interview of the Modest Machine gives a non trivial
Embryo of a Confirmation of Comp in the form of arithmetical quantum logics
To evaluate
comp from its, perhaps startling, consequences, we will adopt a strikingly
naïve methodology: we will interrogate the machine itself. Given that the UDA
reasoning has shown that physics should emerge from a probabilistic structure
bearing on its maximal consistent extensions; it is natural to interrogate the
machine on its consistent extensions. Obviously, to interrogate an arbitrary
machine will not be necessarily interesting. Eventually we will interrogate a
Self-Referentially Correct, Arithmetical Platonist Universal Turing Machine
(SRC machine), and this in the computationalist frame. Precisions will follow.
At first sight such a choice could give the feeling that we are begging the
question, giving that we decide to interview a machine which “share” our
hypotheses. But it is all normal to proceed in this way giving that we are
arguing neither for nor against comp. We are just studying, as in the first
part, the logical consequences of comp. Obviously, at this stage, we can only hope the machine will be able to give
more precise information than the informal (but precise) consequences the non
constructive UDA reasoning has already provide[18].
The naïve methodology invites us to adopt a
naïve stance toward machine’s beliefs. This means we will say a machine
believes a proposition p if and only if the machine asserts p. It is up to us
to choose[19]
a sufficiently chatty machine capable of asserting any of its beliefs, or of
assessing them in a way or another when asked. It is up to us to choose a
sufficiently serious machine. For
example, there is no real problem with a machine asserting that
Presentation of the
machine. A machine will be said Platonist, or Classical,
if 1) the machine believes all classical tautologies, and 2) it is the case
that if the machine ever believes X and ever believes X -> Y, then the
machine will believe Y. I will say the machine is consistent if its set of
belief does not contain a contradiction. f (read false) will abbreviate any
contradiction, like (p & -p) with p denoting some proposition. I will write
Bp as an abbreviation for the proposition according to which the machine
believes p. In the case we would add a proposition p to a consistent set of
machine’s beliefs, then, we will say that the machine remains consistent if the machine does not get a contradiction from
p. So p will be consistent for the machine if -B- p, i.e. the proposition -B- p
is true, i.e. the machine does not prove the negation of p. So we can read -B-
as consistent. For example -B- -p
says that -p is consistent, and this is equivalent to the non believability of
p, i.e. -Bp. The notion of logical consequences of a finite set of propositions
is defined in the usual way[20].
A machine will be said an Arithmetical
Platonist if the machine believes enough elementary arithmetical truth
(including some scheme of induction axiom). A machine will be self-referentially correct, or
self-accurate, when any proposition the machine ever believes about its own
beliefs or consistency propositions, are correct, and this, when B is
translated or encoded in some manner in its language, for example arithmetic. A
machine will be said Universal, if
the machine is able to emulate any computation. For being universal, it is
enough, for a classical arithmetical Platonist machine, to believe all true
Sigma1 propositions. I recall they have the shape “it exists n such that P(n)”.
With the induction axioms such machine will have enough introspective power to
“know” (in the sense of “correctly believe”) that there are universal; in the
sense that they will believe p -> Bp for any p arithmetical Sigma1
proposition. This will eventually provide us a very simple way to translate the
computationalist hypothesis in the machine language, by adding the belief
p->Bp to the machine’s beliefs, identifying the atomic belief with a notion
of DU accessibility.
The fact that we ask “B” to be translated in
the machine language, that is, in term of object the machine is able to handle,
like numbers, makes the machine beliefs “scientific” i.e. third person
communicable (assertable) beliefs. It also protects us against Quine’s form of
essentialism accusation. The machine talks about some description of itself
like an experiencer talks in a third person external way about a description of
its body with its surgeon, or about its doppelganger after a self-duplication
experiment. This means we will need to
define in the machine language the notion of first person points of view. This
will be done later by using the traditional definition given by Theaetetus to
Socrates, and variants, in Plato’s Theaetetus.
Gödel, Minds and
Machines. It is
known, and we will see why below, that all
machines suffer from some intrinsic limitations which are related in particular
to the difference, discovered by Gödel[21],
between truth and provability. An
important literature bears on the impact of Gödel’s results, on the limitation
of formal systems, on the question of mechanism. There are those who, like
Lucas and Penrose, think that the Gödelian incompleteness show we are not
machines, those who doubt any positive or negative relationship can be done,
and those who believe and argue that Gödel’s theorem is really a chance for
mechanism. We belong, like Judson Webb, quasi by construction, to that last
category. Giving that the incompleteness is a direct consequence of Church
thesis, as we have shown, and giving that Gödel has proven his incompleteness
theorem without CT, Judson Webb concludes, in a remarkable book, that
incompleteness could not have been a luckier discovery for the mechanist: it is
a confirmation of CT. And it makes CT a vaccine which protects universal
machines against abusive diagonalisation. Eventually it protects Grand-Mother
against Mister Theory!
No logician, as far as I know, has ever been
convinced by Lucas or Penrose use of Gödel’s results against mechanism[22].
Some genuine reconstructions of Lucas argument have been proposed, and a
consensus exists that incompleteness can be used to show that if we are consistent machines then we cannot know which machine we
are, and a fortiori in which computational history we are most probably
supported by![23] Even Penrose acknowledges this fundamental
nuance in his second best seller book bearing on that question, but, curiously
does not take the nuance into account.
At first sight UDA, which forces us to capture
physics through a measure on the consistent extensions of a SRC machine, could
apparently leads us to some conflict with the second incompleteness theorem
(which will be proved below). It says that a SRC machine cannot believe its own
consistency, -B(-Bf) is true on such machine, so that if you ask such a machine if she has (at
least) one consistent extension, she remains silent! And without any caution
the machine just crash, again! Fortunately, if we are patient and let the SRC
machine dovetail on its beliefs justifications, sooner or later it will
“explain” its silence by asserting that -Bf
-> -B-Bf, that is the machine believes that if she is consistent she
can’t believe in its consistency.
Gödel’s
first incompleteness discovery was indeed that any machine capable of proving
arithmetical theorems either proves falsities or is incapable to prove some
true arithmetical proposition. The lesson is that whatever the machine we
choose; truth will always extend properly its formal (sharable, checkable)
provability abilities. But how to interrogate the machine on the geometry of
its ignorance, as defined by its set of consistent extensions, if the machine
is so limited. A theoretical shorter
path toward the solution will be offered under the form of a couple of logics
of self-reference, the Solovay provability logics G and G*, and which can be
considered as fruitful and amazing descendant of the Gödel and Löb epoch making
incompleteness theorems. I will try now, borrowing some trick in Smullyan’s
gentle introduction to incompleteness, to convey the main ideas without getting
involved into too many technicalities. I hardly can make a better
recommendation than to invite those who want get some familiarisation with the
notions involved here to study Smullyan’s lovely book.
Smullyan Pedagogy. To explain Gödel’s and Löb’s
theorems[24],
Smullyan proposes a puzzle. There is an island where all natives habitants are
either knight or knave. Knights always tell the truth and knaves always lie.
Some reasoner is visiting the island and some habitant tells him “You will
never know that I am a knight.” What can we deduce[25]?
The reasoner could reason in the following way.
Let us suppose the native is a knave. Then he was lying and this means I will
know he is a knight. But I cannot know
he is a knight when he is a knave, so he cannot be a knave and he is a knight
accordingly. Now we can drive a
contradiction. We know the reasoner has reasoned correctly, so the native is
really a knight and the reasoner believe the native is a knight. So we know that
the reasoner know it is a knight, but then the native was wrong and must be a
knave, and that is a contradiction. By knowing we have meant correctly believe.
We got a paradox! Obviously this is a variant of Epimenides’ Paradox. Now for
letting the reasoner himself obtaining such a paradoxical conclusion we must
suppose some capacity of reasoning. Indeed, as Smullyan very genuinely
explains, no paradox would occur in the case a habitant says to a corpse, or
less extremely a deaf, “you will never know I am a knight.” Indeed in that case
the habitant is a knight and indeed the deaf will not know that, giving that he
does not even hear the question. If you are mentally disabled no paradox occurs
either. Some native tells to you the
same sentence, and you can answer “Ah OK” without deducing anything and no
paradox will occurs. So what are the minimal reasoning abilities to get the
paradox? For this problem, it can be shown that the knowledge of classical
propositional logic is enough together with the assumption that the reasoner is
normal, i.e. that if he knows p then
he knows that he knows p.
The reasoning has shown that in case such an
island ever exists, no native will ever say to a normal knower of classical
logic: “you will never know that I am a knight.” That leads the reasoner to a
frank contradiction. Of course it could also mean the “native” was not a
native, it could have been a joking tourist or a mad explorer disguised into a knave.
Now, suppose a (real) native tells
you instead: “you will never believe
that I am a knight.” What can you deduce? We have followed implicitly the
tradition, which originates in the Theaetetus of Plato, of defining the
knowledge of some proposition p, by the correct belief in that proposition.
That is, by definition, “knowing p” is “believing p” with p true. We can write
Cp = p & Bp, where Cp means to (ever) know p, and Bp means to (ever)
believe p.
Going
from knowledge to belief makes things much more subtle and interesting. Indeed
the paradox above, for example, will occur only if the visitor (which the
habitant is addressing) believes all his beliefs are true. In the case where
indeed all his beliefs are true, the reasoning above will show that the
reasoner can neither believe, nor know for the matter, the very fact that all
his beliefs are true. So if all the propositions Bp -> p are true about you, they cannot all be believed by you. Instead of a paradox, we get an
incompleteness result. And you don’t need really to go on the KK Island; it is
enough some habitant asserts “Mister X or Misses X will never believe I am
knight.” That sentence will be true, although unbelievable by X, independently
of the fact X met such sentence. Imagine a native saying “the Belgians will
never believe I am a knight,” then any Belgian believing in its own accuracy,
i.e. believing in all the propositions Bp -> p, will be inaccurate, even if
the Belgian didn’t know anything about the KK Island. Giving that the use of
“believe” instead of “know” evacuates the paradox, such an island could well exist
and the assertion of their inhabitants could have consequences on our ability
or inability to believe some truth! This is a very weird situation. To reassure
ourselves we can still hope such an island does not exist.
But the purpose of the island was just to build
a fictive situation illustrating easily how someone could meet and believe some
self-referential sentence. That works like this: let k be the proposition that
the native is a knight, and suppose the native asserts p. Then p will be true if
and only if k is true, and if someone believes in the rule of the island (I
recall: all knight tell the truth, all knaves lie, and all habitants are either
a knave or a knight), he will believe the proposition (k <-> p). Now the
proposition “you will never believe I am a knight”, once asserted to a believer
in the island rules will make the self-referential proposition (k <->
-Bk) believed by that believer. Moreover (k <-> - Bk) will be indeed true
in case the rules actually hold on the island.
The point now is that, with or without the KK
Island, machines cannot dispose so easily of the self-referential propositions.
Actually machines cannot dispose of them at all. There is a famous result which
proves this fact, known as the diagonalisation
lemma. So with the diagonal lemma, we can reason as if there were a KK Island, making incomplete any third person
sort of “checkable” belief from honest universal machine. The reader who grants
this can jump the following more technical section.
The
diagonalisation lemma. If you have a
duplicating machine D, which when glued a little bit on any machine M
duplicates it, and paste it a little giving say MM, then, gluing it a little
bit to itself DD will results in DD itself. That is DD produces DD, relatively
to some probable universal computational history. In our chatty approach it is
enough the machine believes elementary substitution relations, like subst(abc,
baX) = [baabc], meaning that the substitution of X in the second argument by
the first argument gives (a description of) the string baabc. The bracket “[“
and “]” are used to represent a description of the final result in term of
object the machine can reason about, like the numbers of our arithmetical
universal machine. If the machine remembers that it is always the first
argument which is substitute in the second argument, she will correctly believe
that subst(aXc, baX) = [baaXc], although it could seem at first a little bit
confusing due to the occurrence of X in the first argument string. So the
machine will believe, and the reader is invited to verify this by hands, that:
subst(subst(X,X),
subst(X,X)) = [subst(subst(X,X), subst(X,X))]
We obtain
an expression which denotes a description of itself. Suppose now you want build
a machine capable to operate some mechanical transformation on itself by
applying some other machine T on itself. All you need is a new machine, which I
still write D, capable, if you present it a machine A as input to apply T on
the result of gluing a little bit A on itself before: DA gives T([AA]). Then DD
will gives T([DD]). Applying this idea
on our chatty substitution leads to an expression capable of producing a
transformation of itself, and this in a way the machine can believe. Let us
take any adjective understandable by the machine. They are called predicates in
logic. For exemple the predicate odd(X) which says that X is odd; for instance,
odd(23) is a true proposition, and odd(24) is false. Odd(X) is easily
understandable by our arithmetical machine: odd(X) <-> there is a number Y
such that X = (2 times Y) + 1.
Let us define 1) T(X) by
odd([subst(X,X)]), and 2) let m = [T(X)]. The machine will believe that T(m) is
equivalent to odd([subst(m,m)]), and thus equivalent to odd([subst(m,
[T(X)])]), by 2, and thus equivalent to odd([subst(m, odd([subst(X,X)])]), thus
equivalent to odd([odd[subst(m,m)]]), thus equivalent to odd([T(m)]). That is:
the machine will believe that the proposition T(m) is equivalent to odd(T(m)).
Let us define the closed formula by T(m) by k: we have that the machine
believes k <-> odd([k]).
So k is true iff its description in
the machine language is odd! Now, the choice of the predicate “odd(X)” didn’t
have any relevant role in the proof, as far as it is definable in the machine
language, and we have illustrate that for any such definable predicate P, there
is a corresponding fixed point sentence k such that the machine believes (k
<-> P([k])).
Theorem: For any predicate A definable in
the machine language, there is a proposition k such that the machine will know
(correctly believe) the proposition (k <-> A([k])). Put in another way,
with simplified notations, for any definable predicate P, the logical equation
X <-> P(X) admits a solution k such that the machine believes k <->
Pk.
The consequences of
the diagonalisation lemma are tremendous The fact is that machines no more need to
visit the KK Island to be troubled by all kinds of self-reference. What happens
with the paradoxes? What if a native just simply says “I am not a knight”. The
traditional way to escape the paradox consists to say no native will ever say
that, giving that otherwise, we would be lead to a thorough contradiction.
Suppose now the notion of knight is definable in the machine language by a
predicate knight(x) meaning that x names a true proposition, so that the
machine believes for any proposition p: p <-> knight(p). Then by the
application of the diagonal lemma on the predicate defined by “not
knight(x)”, there is a k such that the
machine will believe that k is equivalent to the negation of knight(k), itself
equivalent to -k, so the machine will believe k <-> -k: contradiction.
Now, by the diagonalisation lemma assumption,
this means that “knight(x)” or “knave(x)” is just not definable in the language
of the machine. Truth on a machine is unnameable by the machine. This is a
version of Tarski theorem. For the same reason, the paradox we get above when
we met a native telling us “you will not know
I am a knight”, with the corresponding fixed point sentence k <-> -Ck,
shows that consistent machine’s knowledge
is not definable by the consistent machine. What can be said about machine’s beliefs, and in particular about the
third person communicable beliefs of our Platonist SRC machine? From the visit
in the
If Gödel incompleteness theorem is amazing, it
is nothing compared to Löb’s theorem. We first need the following sort of sum
up theorem. It can be shown that the
beliefs of the Platonist universal machine are described by the following
provable (and true with the self-referential interpretation) propositions:
1) If M believes p then M believes Bp (M is normal)
2) M believes Bp -> BBp (M knows
he is normal, we will say M is of type 4)
3) M believes B(p->q) -> (Bp
-> Bq) (M believes he is regular, that is, he knows he follows Modus Ponens,
or MoPo). That formula is named K (for Kripke).
I will say
that a normal machine is a type 4 reasoner when it verifies 1, 2, and 3. Line 1
says that the machine is normal. We can say that Bp->BBp is true for the
machine, given that we interpret Bp by the machine believes p. It can be seen
as a form of self-awareness. The second line says that for all propositions the
machine believes it is normal with
respect to them, this gives still more self-awareness: not only Bp->BBp is
true about the machine (by line 1), but line 2 makes it believed by the machine[26].
Line 3 says that the machine is not only Platonist, in the sense of having a
set of beliefs closed for the modus ponens rule, but actually knows (correctly
believes) it is closed for MoPo.
Revision exercises: Let us says that a machine is accurate or
correct, or sound if Bp->p is true for the machine. Let us say that a
machine is stable if BBp->Bp is true for the machine. Could an accurate
machine believe it is accurate with respect to any proposition? Could a
consistent machine believe in its own stability? You can try to show that for
any consistent normal and stable machine, there is an undecidable proposition,
i.e. a proposition p such that the machine can believe neither p nor –p.
Some useful definitions: A machine M1 is referentially
correct about a machine M2, if every proposition proved by M2 is true for M1
(we suppose that true propositions with no symbol B in it are vacuously
referentially true, for example 1+1=2 is true about everybody). A machine is self-referentially correct if it is
referentially correct about itself. Obviously: SRC implies soundness implies
stability. A machine M1 is referentially
complete on M2 if M1 proves all the propositions which are true for M2. You
might show that self-referential correctness entails self-referential
incompleteness.
Arithmetical
Placebo, Self-Confidence and Modesty
What about a native telling to a reasoner the following much more
positive proposition “You will believe I am a knight”? This is, in KK language,
the question L. Henkin asked to M. H. Löb, which leads Löb to a genuine
astonishing generalisation of Gödel’s theorem. In the language of a
arithmetical classical machine, what can be said about a sentence k saying
about itself provable([k]). Apparently that sentence can be said by a knave
(and be false) or by a knight (and be true). That is quite unlike the Gödel
sentences previously studied, on the type p <-> -Bp, which said about themselves that they are not
provable by M, making them true about
M and unprovable by M, when M is
consistent, and making them undecidable by M, when M is also stable. But the
diagonalisation lemma can strike against, in a deeper and more positive way
than we could expect at first sight.
Let us go back on the KK Island. A type 4
student, that is a normal platonist knowing he is normal, is developing some
anxiousness concerning his end of year exams. The teacher told him not to worry
so much and that his anxiousness was just due to some lack of self-confidence.
He told the student that if he could just believe in the success then he would
succeed. That was not a big help giving the fact that the student is really
lacking such a self- confidence, and so, although he trusts his teacher that if
he could ever believe in success he would succeed, he is, as a matter of fact
not believing in success, and could as well completely fail. The teacher then suggested him to make a
visit to the
Now the student gets really desperate. He
thinks he has got no more evidence that the priestess was a knight than he had
trust in himself at the start. Thinking twice he gets a big relief, though.
Why?
Let s be the proposition that the
student will be successful. The student trusts his teacher so that he believes
Bs -> s. Now he believes in the rule
of the island, so that he believes k <-> (Bk -> s) where k is the
proposition that the priestess is a knight. The student made the following
reasoning: “Let us suppose I will believe she is a knight, then I will believe
what she said, that is Bk -> s (being of type 4, he knows he is regular).
But if I believe she is a knight, I will believe that I believe she is a knight
(being of type 4 he knows he is normal), that is I will believe Bk; so if I
ever believe she is a knight I will believe both Bk and Bk -> s, so by
propositional logic, I will believe s, and because I trust my teacher it means
I will succeed. But that is exactly what the priestess said: if I believe she
is a knight I will succeed. So she told me a true statement! So she is a knight.” Being normal, the student
will now believe she is a knight, and thus believes also what she said, that if
he believes she is a knight he will succeed. So he will believe he will
succeed, and then, if his teacher was right, he will succeed!
Now by the
diagonalisation lemma, there is no need for a universal machine of type 4 to go
on a KK island. It simply exists a fixed point sentence k such that k <->
(Bk -> s), for any proposition s, and the reasoning above gives a proof of Löb’s theorem: If a type 4 machine
believes Bp -> p for some proposition p, then the machine believes p.
A simple “corollary” follows: Gödel’s second
incompleteness theorem: if a type 4 machine is consistent then the machine is
unable to believe she is consistent.
Proof:
consistency is, in the machine language, –Bf. But this is Bf -> f, by PC, as
the reader can verify by a two line truth table. By Löb, if ever the machine
believes Bf -> f, she will believe in f, contradicting the assumed
consistency.
And what about Henkin’s question? It is a direct consequence of Löb’s theorem
that a sentence saying “I am provable by M” is true and provable by M! This
follows from the fact that the proposition p<->Bp entails in particular Bp->p.
Note that Löb’s theorem can be stated as
B(Bp->p)->Bp. This formula is called Löb’s formula, and is named L. That
formula is true for M, but M believes it too. A type 4 universal machine can
even prove what we have just proved, that is:
B(k <->(Bk ->p)) ->
B(Bp->p) -> Bp
And Löb’s
formula follows again by a visit to the KK Island, or more seriously by the
diagonisation lemma on the formula BX->p. Löbian machine has been called
modest by Rohit Parikh, and Löb’s formula is really a modesty formula. The
reason is that the machine will believe its accuracy with respect to p, i.e.
will believe Bp->p, only when it
actually believes p. In which case Bp is obvious from MoPo, given that
(p->(q->p)) is a tautology. So it is hard to imagine how to be more
modest than that.
Definition. A type 4 machine is modest, if it believes
all propositions B(Bp ->p)->Bp. It
can be shown that modesty entails belief in its own normality, and so we will
indifferently called our SRC machine, which is provably modest, a modest or a
Löbian machine[27].
A type 4 universal machine does not need to visit the KK Island to become
modest, by the diagonalisation lemma.
Solovay’s
incompleteness-completeness theorems In 1976, Solovay has given two genuine
and wonderful completeness theorems, concerning the (infinite) discourses we can
have with an arithmetical Platonist SRC machine, or more general Löbian
machines and entity[28].
His first theorem says that modest propositional believability logic, Solovay
named G, that is the normal system with K and L as axioms, formalizes
completely the provable arithmetical
propositional logic of provability and consistency, of Peano arithmetic, or ZF,
actually of any ordinary provability predicate in RE set extending PA. This
makes the L formula really the fundamental formula of machine’s psychology. It
is known that 4 can be derived from L in G.
The second theorem is still more
amazing. We consider the following theory G* which has as axioms all theorems
of G, plus the soundness formula Bp->p. And which is closed for MoPo. Note
that we don’t ask G* being normal, for the reason that, in that case, from the
axiom instantiation Bf->f, normality would lead to B(Bf->f), and
Löbianity would then lead to Bf, and giving we got already Bf->f, MoPo would
lead to f, making G* inconsistent. The second theorem of Solovay says that G*
formalizes completely the true arithmetical propositional logic of provability
and consistency.
Now it can be shown that both G and G* are
decidable, making the G* minus G corona a decidable set, closed for MoPo, of
unbelievable truth. Giving our naïve stance, it makes them non communicable as
well. For example we know that the SRC is consistent, stable and sound, but
cannot know it, and that makes –Bf, BBp->Bp, and Bp->p belonging to G*\G.
In fact, as G is closed for the necessitation rule, G* is closed for the
“possibilization” rule: if p is provable by G*, then -B- p is also provable by
G*. The decidability of G and G* entails[29]
the decidability of all the logics which follow.
Computationalism: It is the computationnalist hypothesis which
has invited us to interview the self-referentially correct machine. Such a
machine could consistently being non computationalist. By incompleteness it is
consistent for a consistent machine to believe in its own inconsistency, indeed
the second incompleteness theorem just says that: -Bf->-B-Bf. We could
interview consistent but non self-referentially correct machine, and actually
we could interview non computationalist machines, who believe they lose their
consistency by doing teleportation. But, as we justify at the start, we are
interested in the discourse of the SRC machine in the comp frame. Self-reference and Solovay theorems did
justifies that atomic, in the
logician sense, propositions corresponds to the arithmetical propositions, and
that makes unavoidable the use of G and G*. Now, to take into account comp and
the UD Argument which shows that the physical propositions arises from a sum of
DU-accessible states, we must restrict those arithmetical propositions to those
proved or generated by the Arithmetical Dovetailer, i.e. the Sigma1 sentences[30]
as explained in the 8th UDA step. Our introspective universal
machine knows that they are universal
in the sense that for any Sigma1 sentence p, the machine can prove that if p is
true then p is provable: they can prove p->Bp. So to restrict, the SRC
discourse in the comp frame, and in that way enrich the self-reference logic,
it is just enough to add to G the sentence p->Bp with p atomic. I like to
call 1 the proposition “p->Bp” with p atomic, due to its fundamental
importance but also as a shortening of Sigma1. “1” can be seen as the comp axiom written as a (scheme of)
formula added to G, and so belonging to the (infinite) discourse of the SRC in the comp frame. In my previous work I
did use only the arithmetical soundness of that new logic, but the logician
Albert Visser (19) did prove the soundness and completeness of G+1, and its
corresponding (G+1)* truth theory. Vickers gives also independent motivations
for a similar notion of verifiability, and I am used to call G+1 and (G+1)*, V
and V* accordingly[31].
Note that the sentence letter p in p->Bp cannot be substitute by any
formula, but only by propositional letter, if we want keep correct the
arithmetical discourse interpretation. By way of counterexample p->Bp would
be in contradiction with incompleteness in case p is replaced by –Bf.
If you identify a logic with its set of
theorems you have the following diamond, which I will call the basic diamond
for further reference. The implicit edges represent inclusion:
V*
G* V
G
Going up in
the
Arithmetical
Theaetetus. We are not yet in a position to get physics.
What is missing is the fundamental distinction between the first and third
person points of view, without which the UD Argument just doesn't start. The
four G, G*, V, V* gives only 3rd person descriptions. G for example axiomatizes
completely the propositional logic of self-referentially correct discourse made
by Platonist machines, but those machines talk about themselves only through
third person description made (by construction) at the right level. For
instance Peano arithmetic provability is described in term of numbers, often
called Gödel Numbers.
But the Universal Dovetailer Argument (UDA) did
show that physics must appear through the machine's first person point of view,
or from some first person plural point of views. Those first person points of
view concern anticipations of consistent extensions from some personal,
interrogative, perhaps unconscious most of the time but made conscious in front
of the comp doctor, bet on self-consistency.
To interrogate the Universal Machine
we need to define those points of views from what the machine is able to talk
on. We will follow two ideas and their union: 1) to define the first person by
the knower, i.e. the one who correctly believes the propositions. This is one
of the well known (by philosophers) Theaetetus attempts to define knowledge
from opinion after Socrates asked him, in Plato’s Theaetetus. 2) to define the
first person (plural ?) by the better. With the first idea we give to the
believer an unbreakable umbilical cord with truth, making it incorrigible as a
knower should be. With the second idea we attach the believer to some
(hopefully correct) bet on his own consistency. At least formally, we can
imagine uniting those two ideas for getting the correct better. All three ideas can be defined in the propositional
self-reference logic:
To know p, written Cp, is defined
by Bp & p,
To bet on p, written Pp, is defined
by Bp & -B-p,
To correctly bet on P, written Op,
is defined by Bp & -B-p & p.
This makes
sense: G* proves indeed that Bp is equivalent to Cp, and to Pp, and to Op, but
from the machine point of view, (Bp <-> Cp), i.e. (Bp <-> Bp &
p) is neither believable, nor knowable, that is provable by G; nor are the G*
equivalence (Bp <-> Pp) and (Bp <-> Op), (Pp <-> Op) provable
by G. This follows from the simple facts
that G*, unlike G, proves Bp ->p, and
G* proves p->-B-p. All arithmetical realisations of the corresponding modal
logics, where the sentence letter are interpreted by arithmetical sentences,
prove the same arithmetical sentences, but from the machine point of view they
give very different logics. Those variants of Theaetetus’ definition describe
different ways a machine can be related to truth, and those ways are
ontic-equivalent (by G*), but epistemic-non-equivalent (by G). And all those
G/G* remarks can be lifted with the comp V/V* constraints, where the sentence
letters are interpreted by Sigma1 sentences. So, by applying the three
Theaetetus variants on each logics taken from the basic diamond, we get 12
logics. Actually we get 10 logics, because two of the logics obtained can be
shown to be equal: G* and G give the same knower (Cp), and V* and V give the
same “comp-knower”. This means that from the point of view of the knower,
believability is equated to truth. It makes it akin to a constructivist
self-extending self. Like in Brouwer’s consciousness theory[33],
that self is unnameable by itself, and this follows from the fact that Cp, as
it has been showed, is no definable by the machine. So the knower cannot really
believe he is any third person nameable machine, and this could explain some
reluctance of the first person to bet on an artificial digital body or to fear
digital duplication. The application of the CP variants on G(*)
has been well studied in the literature. It has been done independently by
Boolos, Goldblatt, and Kuznetsov and Muravitski. Artemov makes it a thesis[34].
It gives a logic of irreversible (antisymmetric) subjective “time” quite
similar again in that respect with Brouwer’s consciousness theory. And this has
been confirmed (not proved!) by a result of Goldblatt, itself (related to some
work of Gödel and McKinsey & Tarski), relating S4Grz (read S4 Grzegorczyk,
it is the result of the CP variant on G(*)) and
intuitionist logic. Let us note that philosophers who don’t accept the
Cp-Theaetetus definition of knowledge, implicitly or explicitly pretend to be
able to distinguish the waking state from the dreaming state, and so, negate
the most primitive form of comp, as was suggested by the step 6 in UDA. As an
example, the positivist philosopher Malcolm attempts to refute[35]
both the existence of consciousness in dream and in machine. He compares the lucid dream proposition “I dream” with
the Epimenides’ lying sentence “I lie,” G and G* make possible finer
comparisons. S4grz is an abyss of interesting things to say on the machine’s
first person psychology, but I will refer the reader to my “Conscience et
Mécanisme” for more information, because it is about time to look at physics
and sensations.
Physics
and Sensation To get physics and sensations we must apply the Theaetetus
variants on V*. It is the only way to find the “true” logic of a probability
measure on all consistent extensions
(this explains the star *), arising when the atomic propositions are restricted
on those accessible by the Universal Dovetailer (the Sigma1 one, this explains
the V = G+1).
To get a modal logic featuring a
probability notion, both model theory and modal semantics, which are a little
bit beyond the scope of this paper, suggests the need of having the deontic
formula Np -> -N-p, where N is an abstract necessity modality at first. The
idea is that Np means P(p) = 1, with P(p) interpreted as a probability of p,
and then -P(-p) means “P(-p) is
different of 1” which means “P(p) is different of 0”, which makes the deontic
formula natural for a probability notion. Note that neither G nor G* does prove
it (G* does not prove Bf->-B-f, indeed G* proves Bf->B-f). Now all logics
obtained by an application of the Theaetetus variants give a logic verifying
the deontic probabilistic formula. Naturally the Pp-variant is the literal
translation of the consequence of UDA, so it should, with the comp hypothesis,
give the physical probability. So the Pp variant, which gives a modal logic
featuring the “probability one” or the “measure one” on the consistent
extensions should give a logic of measure one on the physical propositions. So
we need to look about what the physicist says on such a logic, and to look what
the Pp variant on V* says, and then compare.
I said at the beginning that Quantum
Physics was a good candidate for being a stable part of fundamental physics.
Now quantum physics is essentially a probability calculus. Von Neumann worked
out, with the help of Birkhoff, a logic of quantum probability one. In quantum physics, worlds or
states are represented by line in a Hilbert space. Propositions are represented
by linear subspace. Like Boolean classical logic can be interpreted as a
lattice of subsets of a set, and like Brouwerian intuitionist Logic can be
interpreted as the lattice of open sets of a topological space, Quantum Logic
can be interpreted as a lattice of subspaces of a Hilbert (complex linear)
space. Each “sub-notion” can, from a modal angle, be considered as both a
proposition and as the “collection” of worlds in which that proposition is
true. Modularity of the lattice (a weakening of the Boolean distributivity)
gives hope to von Neumann of capturing a complete logic of yes-no orthogonal
experiments capable of yielding all the quantum probabilities. Alas, infinite
dimension kills modularity, and von Neumann will jump from the Hilbert space to
the… von Neumann algebras. Still, he will remain unsatisfied with the quantum
logics he will isolate[36],
and, as van Fraassen wrote, physicists are confronted with a labyrinth of quantum logics.
So, to be honest, I don’t know yet
if it is a good news or a bad news, for those wanting comp being confirmed or
being refuted, but, not only Pp, but also Op, and even Cp, when applied on V*
leads to bizarre and different sorts of arithmetical quantum logics. How?
Definition
A modal quasi-quantum logic has as main axiom, p->BMp (p atomic). I like to
call that formula “LASE” for “Little Abstract Schrödinger Equation”. M is an
abbreviation of -B-. A modal quasi-quantum logic has also the axiom Bp ->p
(T), with K B(p->q)->(Bp->Bq),
and is closed for MoPo, but not necessarily the necessitation inference rule (=
is not necessarily normal).
Why?
Goldblatt has shown that the logic B, known as the Brouwersche System, and
which is the modal logic with K, B(p->q)->(Bp->Bq), and LASE, p->BMp, and T, Bp->p, and
which is normal, axiomatizes quantum
logic (in the classical setting), in a similar way as S4Grz axiomatized
intuitionist logic (in the classical setting).
Precisely,
considering the following transformation GOLDB, due to Goldblatt 1974, from the
propositional language to the modal propositional language, which transforms
sentence letters p into BMp, and transforms -p into B-p, and transforms
recursively (A & B) into (GOLDB A & GOLDB B), Goldblatt showed[37]
that a formula A is proved in a minimal version of quantum logic iff B proves GOLDB(A).
Now, the
modal quasi quantum logics have, thanks to the truth of LASE for the atomic
propositions, all what is needed to be able to apply the Goldblatt
transformation for getting reasonable arithmetical quantum logics. Applying the
Cp, Pp, and Op Theaetetus variants on the basic logics diamond, gives, as we
expected from UDA with at least the Pp variants, three modal quasi-quantum
logics. They are the one called S4Grz1, Z1*, X1* respectively, in my PhD thesis
“Calculabilite, Physique et Cognition[38]”.
S4Grz1 Z1* X1*
S4Grz S4Grz1 Z* Z1 X* X1
S4Grz Z X
Applying
the (inverse) Goldblatt transform on S4Grz1, Z1*, X1* gives the three
arithmetical quantum logics AQL0 , AQL1, AQL2 leading to many open problems. Do we have
modularity, or orthomodularity, or something else? Are the
I conjecture a quantum computer can be defined
in the AQLi, or in their first order extensions (with quantifiers).
This would explain why any universal machine looking at itself discovers a
quantum “reality” as a measure on its most probably correct anticipations.
When applying the Goldblatt transform on the
non empty collection of propositions Z1* minus Z1, and X1* minus X1, this gives
a description of the consistent (and true) comp-physically measurable but uncommunicable truth, so that the
“qualia” or sensations, are themselves described by sorts of quantum logics[39].
It is the main advantage of comp, compared to traditional empirical physics.
Empirical physics is obviously in advance compared to the comp physics, but is
quasi obliged, by methodology, to put the first person under the rug, and so
misses the Qualia Logics.
Comp makes them possible and necessary, and
isolates them from the many modal nuances imposed by Löbian incompleteness.