Difference between revisions of "Particle Swarm Optimization - Scholarpedia Draft"
| (56 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <strong>Particle swarm optimization</strong> (PSO) is a population-based |
+ | <strong>Particle swarm optimization</strong> (PSO) is a population-based |
| + | stochastic approach for solving continuous and discrete optimization problems. |
||
| − | In particle swarm optimization, simple software agents, called ''particles'' move in the solution space of an optimization problem. The position of a particle represents a candidate solution to the optimization problem at hand. Particles search for better positions in the solution space by changing their velocity according to rules originally inspired by behavioral models of bird flocking. |
+ | In particle swarm optimization, simple software agents, called ''particles'', move in the solution space of an optimization problem. The position of a particle represents a candidate solution to the optimization problem at hand. Particles search for better positions in the solution space by changing their velocity according to rules originally inspired by behavioral models of bird flocking. |
Particle swarm optimization belongs to the class of [[swarm intelligence]] techniques that are used to solve optimization problems. |
Particle swarm optimization belongs to the class of [[swarm intelligence]] techniques that are used to solve optimization problems. |
||
| Line 9: | Line 10: | ||
Particle swarm optimization was introduced by Kennedy and Eberhart (1995). It has roots in the simulation of social behaviors using tools and ideas taken from computer graphics and social psychology research. |
Particle swarm optimization was introduced by Kennedy and Eberhart (1995). It has roots in the simulation of social behaviors using tools and ideas taken from computer graphics and social psychology research. |
||
| − | Within the field of computer graphics, the first antecedents of particle swarm optimization can be traced back to the work of Reeves (1983), who proposed particle systems to model objects that are dynamic and cannot be easily represented by polygons or surfaces. Examples of such objects are fire, smoke, water and clouds. In these models, particles are independent of each other and |
+ | Within the field of computer graphics, the first antecedents of particle swarm optimization can be traced back to the work of Reeves (1983), who proposed particle systems to model objects that are dynamic and cannot be easily represented by polygons or surfaces. Examples of such objects are fire, smoke, water and clouds. In these models, particles are independent of each other and |
| + | their movement is governed by a set of rules. Some years later, Reynolds (1987) used a particle system to simulate the collective behavior of a flock of birds. In a similar kind of simulation, Heppner and Grenander (1990) included a ''roost'' that was attractive to the simulated birds. Both models inspired the set of rules that were later used in the original particle swarm optimization algorithm. |
||
| − | Social psychology research was another source of inspiration in the development of the first particle swarm optimization algorithm. The rules that govern the movement of the particles in a problem's solution space can also be seen as a model of human social behavior in which individuals adjust their beliefs and attitudes to conform with those of their peers (Kennedy & Eberhart 1995). |
+ | Social psychology research, in particular the dynamic theory of social impact (Nowak, Szamrej & Latané, 1990), was another source of inspiration in the development of the first particle swarm optimization algorithm (Kennedy, 2006). The rules that govern the movement of the particles in a problem's solution space can also be seen as a model of human social behavior in which individuals adjust their beliefs and attitudes to conform with those of their peers (Kennedy & Eberhart 1995). |
| − | |||
| − | <!--The name ''particle swarm'' was chosen because the collective behavior of the particles adheres to the principles described by Millonas (1994).--> |
||
== Standard PSO algorithm == |
== Standard PSO algorithm == |
||
=== Preliminaries === |
=== Preliminaries === |
||
| − | The problem of minimizing |
+ | The problem of minimizing<math>^1</math> |
the function <math>f: \Theta \to \mathbb{R}</math> with <math>\Theta \subseteq \mathbb{R}^n</math> can be stated as finding the set |
the function <math>f: \Theta \to \mathbb{R}</math> with <math>\Theta \subseteq \mathbb{R}^n</math> can be stated as finding the set |
||
| − | <math>\Theta^* = \underset{\vec{\theta} \in \Theta}{\operatorname{arg\,min}} |
+ | <math>\Theta^* = \underset{\vec{\theta} \in \Theta}{\operatorname{arg\,min}} |
| + | \, f(\vec{\theta}) = \{ \vec{\theta}^* \in \Theta \colon f(\vec{\theta}^*) |
||
| + | \leq f(\vec{\theta}), \,\,\,\,\,\,\forall \vec{\theta} \in \Theta\}\,,</math> |
||
| − | where <math>\vec{\theta}</math> is an <math>n</math>-dimensional vector that belongs to the set of feasible solutions <math>\Theta</math> (also called solution space). |
+ | where <math>\vec{\theta}</math> is an <math>n</math>-dimensional vector that belongs to the set of feasible solutions <math>\Theta</math> (also called solution space). |
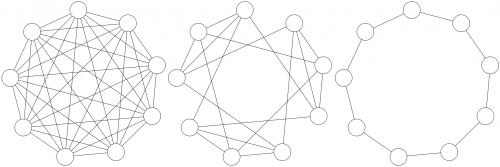
| − | [[Image: |
+ | [[Image:PSOTopologies-9.png|thumb|500px|right|Example population topologies. The leftmost picture depicts a fully connected topology, that is, <math>\mathcal{N}_i = \mathcal{P}\,\,\forall p_i \in \mathcal{P}</math> (self-links are not drawn for simplicity) . The picture in the center depicts a so-called von Neumann topology, in which <math>|\mathcal{N}_i| = 4\,\,\forall p_i \in \mathcal{P}</math>. The rightmost picture depicts a ring topology in which each particle is neighbor to two other particles.]] |
| + | In PSO, the so-called ''swarm'' is composed of a set of particles |
||
| − | Let <math>\mathcal{P} = \{p_{1},p_{2},\ldots,p_{k}\}</math> be the population of particles (also referred to as ''swarm''). |
||
| + | <math>\mathcal{P} = \{p_{1},p_{2},\ldots,p_{k}\}</math>. A particle's position |
||
| − | At any time step <math>t</math>, a particle <math>p_i</math> has a position <math>\vec{x}^{\,t}_i</math> and a velocity <math>\vec{v}^{\,t}_i</math> associated to it. The best position that particle <math>p_i</math> has ever visited until time step <math>t</math> is represented by vector <math>\vec{b}^{\,t}_i</math> (also known as a particle's ''personal best''). Moreover, a particle <math>p_i</math> receives information from its ''neighborhood'', which is defined as the set <math>\mathcal{N}_i \subseteq \mathcal{P}</math>. Note that a particle can belong to its own neighborhood. In the standard particle swarm optimization algorithm, the particles' neighborhood relations are commonly represented as a graph <math>G=\{V,E\}</math>, where each vertex in <math>V</math> corresponds to a particle in the swarm and each edge in <math>E</math> establishes a neighbor relation between a pair of particles. The resulting graph is commonly referred to as the swarm's ''population topology''. |
||
| + | represents a candidate solution of the considered optimization problem |
||
| + | represented by an objective function <math>f</math>. At any time step |
||
| + | <math>t</math>, <math>p_i</math> has a position <math>\vec{x}^{\,t}_i</math> |
||
| + | and a velocity <math>\vec{v}^{\,t}_i</math> associated to it. The best |
||
| + | position that particle <math>p_i</math> (with respect to <math>f</math>) has |
||
| + | ever visited until time step <math>t</math> is represented by vector |
||
| + | <math>\vec{b}^{\,t}_i</math> (also known as a particle's ''personal best''). |
||
| + | Moreover, a particle <math>p_i</math> receives information from its |
||
| + | ''neighborhood'' <math>\mathcal{N}_i \subseteq \mathcal{P}</math>. In the |
||
| + | standard particle swarm optimization algorithm, the particles' neighborhood |
||
| + | relations are commonly represented as a graph <math>G=\{V,E\}</math>, where |
||
| + | each vertex in <math>V</math> corresponds to a particle in the swarm and each |
||
| + | edge in <math>E</math> establishes a neighbor relation between a pair of |
||
| + | particles. The resulting graph is commonly referred to as the swarm's ''population topology'' (Figure 1). |
||
=== The algorithm === |
=== The algorithm === |
||
| − | The algorithm starts with the random |
+ | The PSO algorithm starts with the random generation of the particles' positions within an initialization region |
| − | <math>\Theta^\prime \subseteq \Theta</math>. During the main loop of the algorithm, the particles' velocities and positions |
+ | <math>\Theta^\prime \subseteq \Theta</math>. Velocities are usually initialized within <math>\Theta^\prime</math> but they can also be initialized to zero or to small random values to prevent them leaving the search space during the first iterations. During the main loop of the algorithm, the particles' velocities and positions are iteratively updated until a stopping criterion is met. |
| − | are iteratively updated until a stopping criterion is met. |
||
| − | The |
+ | The update rules are: |
<math>\vec{v}^{\,t+1}_i = w\vec{v}^{\,t}_i + \varphi_2\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i) \,,</math> |
<math>\vec{v}^{\,t+1}_i = w\vec{v}^{\,t}_i + \varphi_2\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i) \,,</math> |
||
| Line 41: | Line 56: | ||
<math>\vec{x}^{\,t+1}_i = \vec{x}^{\,t}_i +\vec{v}^{\,t+1}_i \,,</math> |
<math>\vec{x}^{\,t+1}_i = \vec{x}^{\,t}_i +\vec{v}^{\,t+1}_i \,,</math> |
||
| + | where <math>w</math> is a parameter called ''inertia weight'', |
||
| − | where <math>w</math> is a parameter called ''inertia weight'', <math>\varphi_1</math> and <math>\varphi_2</math> are two parameters called ''acceleration coefficients'', <math>\vec{U}^{\,t}_1</math> and <math>\vec{U}^{\,t}_2</math> are two <math>n \times n</math> diagonal matrices with in-diagonal elements distributed in the interval <math>[0,1)\,</math> uniformly at random. Every iteration, these matrices are regenerated, that is, <math>\vec{U}^{\,t+1}_{1,2} \neq \vec{U}^{\,t}_{1,2}</math>. Vector <math>\vec{l}^{\,t}_i</math> is the best position ever found by any particle in the neighborhood of particle <math>p_i</math>, that is, <math>f(\vec{l}^{\,t}_i) \leq f(\vec{b}^{\,t}_j) \,\,\, \forall p_j \in \mathcal{N}_i</math>. |
||
| + | <math>\varphi_1</math> and <math>\varphi_2</math> are two parameters called |
||
| + | ''acceleration coefficients'', <math>\vec{U}^{\,t}_1</math> and |
||
| + | <math>\vec{U}^{\,t}_2</math> are two <math>n \times n</math> diagonal matrices |
||
| + | in which the entries in the main diagonal are distributed in the interval |
||
| + | <math>[0,1)\,</math> uniformly at random. At every iteration, these matrices |
||
| + | are regenerated. Usually, vector <math>\vec{l}^{\,t}_i</math>, |
||
| + | referred to as the ''neighborhood best,'' is the best position ever found by |
||
| + | any particle in the neighborhood of particle <math>p_i</math>, that is, |
||
| + | <math>f(\vec{l}^{\,t}_i) \leq f(\vec{b}^{\,t}_j) \,\,\, \forall p_j \in |
||
| + | \mathcal{N}_i</math>. If the values of <math>w</math>, <math>\varphi_1</math> and <math>\varphi_2</math> are properly chosen, it is guaranteed that the particles' velocities do not grow to infinity (Clerc and Kennedy 2002). |
||
| + | |||
| + | The three terms in the velocity update rule characterize the local behaviors that particles follow. The first term, called the ''inertia'' or |
||
| + | ''momentum'' serves as a memory of the previous flight direction, preventing |
||
| + | the particle from drastically changing direction. The second term, called the |
||
| + | ''cognitive component'' resembles the tendency of particles to return to |
||
| + | previously found best positions. The third term, called the ''social component'' |
||
| + | quantifies the performance of a particle relative to its |
||
| + | neighbors. It represents a group norm or standard that should be attained. |
||
| + | |||
| + | In some cases, particles can be attracted to regions outside the feasible search space <math>\Theta</math>. For this reason, mechanisms for preserving solution feasibility and a proper swarm operation have been devised (Engelbrecht 2005). One of the least disruptive mechanisms for handling constraints is one in which particles going outside <math>\Theta</math> are not allowed to improve their personal best position so that they are attracted back to the feasible space in subsequent iterations. |
||
A pseudocode version of the standard PSO algorithm is shown below: |
A pseudocode version of the standard PSO algorithm is shown below: |
||
<code> |
<code> |
||
| − | :'''Inputs''' ''Objective function <math>f:\Theta \to \mathbb{R}</math>, the initialization domain <math>\Theta^\prime \subseteq \Theta</math>, |
+ | :'''Inputs''' ''Objective function <math>f:\Theta \to \mathbb{R}</math>, the initialization domain <math>\Theta^\prime \subseteq \Theta</math>, |
| − | + | the number of particles <math>|\mathcal{P}| = k</math>, the parameters <math>w</math>, <math>\varphi_1</math>, and <math>\varphi_2</math>, and the stopping criterion <math>S</math>'' |
|
:'''Output''' ''Best solution found'' |
:'''Output''' ''Best solution found'' |
||
| Line 54: | Line 89: | ||
for i := 1 to k do |
for i := 1 to k do |
||
Initialize <math>\mathcal{N}_i</math> to a subset of <math>\mathcal{P}</math> according to the desired topology |
Initialize <math>\mathcal{N}_i</math> to a subset of <math>\mathcal{P}</math> according to the desired topology |
||
| − | Initialize <math>\vec{x |
+ | Initialize <math>\vec{x}^{\,t}_i</math> randomly within <math>\Theta^\prime</math> |
| + | Initialize <math>\vec{v}^{\,t}_i</math> to zero or a small random value |
||
Set <math>\vec{b}^{\,t}_i = \vec{x}^{\,t}_i</math> |
Set <math>\vec{b}^{\,t}_i = \vec{x}^{\,t}_i</math> |
||
end for |
end for |
||
| Line 63: | Line 99: | ||
// Velocity and position update loop |
// Velocity and position update loop |
||
for i := 1 to k do |
for i := 1 to k do |
||
| − | Set <math>\vec{l}^{\,t}_i</math> := <math> |
+ | Set <math>\vec{l}^{\,t}_i</math> := <math>\underset{{\vec{b}^{\,t}}_j \in \Theta \,|\, p_j \in \mathcal{N}_i}{\operatorname{arg\,min}} \, f({\vec{b}^{\,t}}_j)</math> |
| − | Generate random matrices <math>\vec{U}^{\,t}_1</math> and <math>\vec{U}^{\,t} |
+ | Generate random matrices <math>\vec{U}^{\,t}_1</math> and <math>\vec{U}^{\,t}_2</math> |
Set <math>\vec{v}^{\,t+1}_i</math> := <math>w\vec{v}^{\,t}_i + \varphi_1\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i)</math> |
Set <math>\vec{v}^{\,t+1}_i</math> := <math>w\vec{v}^{\,t}_i + \varphi_1\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i)</math> |
||
Set <math>\vec{x}^{\,t+1}_i</math> := <math>\vec{x}^{\,t}_i + \vec{v}^{\,t+1}_i</math> |
Set <math>\vec{x}^{\,t+1}_i</math> := <math>\vec{x}^{\,t}_i + \vec{v}^{\,t+1}_i</math> |
||
| Line 71: | Line 107: | ||
// Solution update loop |
// Solution update loop |
||
for i := 1 to k do |
for i := 1 to k do |
||
| − | if <math>f(\vec{x}^{\,t}_i) |
+ | if <math>f(\vec{x}^{\,t}_i) < f(\vec{b}^{\,t}_i)</math> |
Set <math>\vec{b}^{\,t}_i</math> := <math>\vec{x}^{\,t}_i</math> |
Set <math>\vec{b}^{\,t}_i</math> := <math>\vec{x}^{\,t}_i</math> |
||
end if |
end if |
||
| Line 80: | Line 116: | ||
end while |
end while |
||
</code> |
</code> |
||
| + | |||
| + | The algorithm above follows synchronous updates of particle positions and best |
||
| + | positions, where the best position found is updated only after all particle |
||
| + | positions and personal best positions have been updated. In asynchronous |
||
| + | update mode, the best position found is updated immediately after each |
||
| + | particle's position update. Asynchronous updates have a faster propagation of |
||
| + | best solutions through the swarm. |
||
== Main PSO variants == |
== Main PSO variants == |
||
| Line 87: | Line 130: | ||
=== Discrete PSO === |
=== Discrete PSO === |
||
| − | Most particle swarm optimization algorithms are designed to search in continuous domains. However, there are a number of variants that operate in discrete spaces. The first variant that worked on discrete domains was the binary particle swarm optimization algorithm (Kennedy and Eberhart 1997). In this algorithm, a particle's position is discrete but its velocity is continuous. The <math>j</math>th component of a particle's velocity vector is used to compute the probability with which the <math>j</math>th component of the particle's position vector takes a value of 1. Velocities are updated as in the standard PSO algorithm, but positions are updated using the following rule |
+ | Most particle swarm optimization algorithms are designed to search in continuous domains. However, there are a number of variants that operate in discrete spaces. The first variant that worked on discrete domains was the binary particle swarm optimization algorithm (Kennedy and Eberhart 1997). In this algorithm, a particle's position is discrete but its velocity is continuous. The <math>j</math>th component of a particle's velocity vector is used to compute the probability with which the <math>j</math>th component of the particle's position vector takes a value of 1. Velocities are updated as in the standard PSO algorithm, but positions are updated using the following rule: |
<math> |
<math> |
||
| Line 97: | Line 140: | ||
</math> |
</math> |
||
| − | where <math>r</math> is a uniformly distributed random number in the range <math>[0,1)\,</math> and |
+ | where <math>x_{ij}</math> is the <math>j</math>th component of the position vector of particle <math>p_i</math>, <math>r</math> is a uniformly distributed random number in the range <math>[0,1)\,</math> and |
<math> |
<math> |
||
| Line 103: | Line 146: | ||
</math> |
</math> |
||
| + | === Constriction Coefficient === |
||
| − | Other approaches to tackle discrete problems include transforming the continuous domain into discrete sets of intervals (Fukuyama et al. 1999), rounding off the components of the particles' position vectors (Laskari et al. 2002), and redefining the mathematical operators used in the velocity- and position-update rules to suit a chosen problem representation (Clerc 2004). |
||
| + | The ''constriction coefficient'' was introduced as an outcome of a theoretical |
||
| − | === Bare bones PSO === |
||
| + | analysis of swarm dynamics (Clerc and Kennedy 2002). Velocities |
||
| + | are constricted, with the following change in the velocity update: |
||
| + | <math>\vec{v}^{\,t+1}_i = \chi^t[\vec{v}^{\,t}_i + |
||
| + | \varphi_2\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + |
||
| + | \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i)]</math> |
||
| + | where <math>\chi^t</math> is an <math>n \times n</math> diagonal matrix in |
||
| + | which the entries in the main diagonal are calculated as |
||
| + | |||
| + | <math>\chi^t_{jj}=\frac{2\kappa}{|2-\varphi^t_{jj}-\sqrt{\varphi^t_{jj}(\varphi^t_{jj}-2)}|}</math> |
||
| + | with <math>\varphi^t_{jj}=\varphi_1U^t_{1,jj}+\varphi_2U^t_{2,jj}</math>. Convergence is guaranteed under |
||
| + | the conditions that <math>\varphi^t_{jj}\ge 4\,\forall j</math> and <math>\kappa\in |
||
| + | [0,1]</math>. |
||
| + | |||
| + | === Bare-bones PSO === |
||
The ''bare-bones particle swarm'' (Kennedy 2003) is a variant of the particle swarm optimization algorithm in which the velocity- and position-update rules are substituted by a procedure that samples a parametric probability density function. |
The ''bare-bones particle swarm'' (Kennedy 2003) is a variant of the particle swarm optimization algorithm in which the velocity- and position-update rules are substituted by a procedure that samples a parametric probability density function. |
||
| − | In the bare |
+ | In the bare-bones particle swarm optimization algorithm, a particle's position update rule in the <math>j</math>th dimension is |
<math> |
<math> |
||
| − | x^{t+1}_{ij} = N\left(\ |
+ | x^{t+1}_{ij} = N\left(\mu_{ij}^{t} ,\sigma_{ij}^{\,t}\right)\,, |
</math> |
</math> |
||
where <math>N</math> is a normal distribution with |
where <math>N</math> is a normal distribution with |
||
| Line 117: | Line 174: | ||
<math> |
<math> |
||
\begin{array}{ccc} |
\begin{array}{ccc} |
||
| − | \ |
+ | \mu_{ij}^{t} &=& \frac{b^{t}_{ij} + l^{t}_{ij}}{2} \,, \\ |
| − | \ |
+ | \sigma_{ij}^{t} & = & |b^{t}_{ij} - l^{t}_{ij}| \,. |
\end{array} |
\end{array} |
||
</math> |
</math> |
||
| − | |||
| − | Although a normal distribution was chosen when it was first proposed, any other probability density function can be used with |
||
| − | the bare bones model as done by Richter and Blackwell (2006). |
||
=== Fully informed PSO === |
=== Fully informed PSO === |
||
| Line 134: | Line 188: | ||
\vec{v}^{\,t+1}_i = w\vec{v}^{\,t}_i + \frac{\varphi}{|\mathcal{N}_i|}\sum_{p_j \in \mathcal{N}_i}\mathcal{W}(\vec{b}^{\,t}_j)\vec{U}^{\,t}_j(\vec{b}^{\,t}_j-\vec{x}^{\,t}_i) \,, |
\vec{v}^{\,t+1}_i = w\vec{v}^{\,t}_i + \frac{\varphi}{|\mathcal{N}_i|}\sum_{p_j \in \mathcal{N}_i}\mathcal{W}(\vec{b}^{\,t}_j)\vec{U}^{\,t}_j(\vec{b}^{\,t}_j-\vec{x}^{\,t}_i) \,, |
||
</math> |
</math> |
||
| + | where <math>\mathcal{W} \colon \Theta \to [0,1]</math> is a function that weighs the contribution of a particle's personal best position to the movement of the target particle based on its relative quality. |
||
| + | == Applications of PSO and Current Trends== |
||
| − | where <math>w</math> is a parameter called the ''inertia weight'', <math>\varphi</math> is a parameter called ''acceleration coefficient'', and <math>\mathcal{W} \colon \Theta \to [0,1]</math> is a function that weighs the contribution of a particle's personal best position to the movement of the target particle based on its relative quality. |
||
| + | The first practical application of a PSO algorithm was in the field of neural |
||
| − | == Applications of PSO == |
||
| + | network training and was published together with the algorithm itself (Kennedy |
||
| + | and Eberhart 1995). Many more areas of application have been explored ever |
||
| + | since, including telecommunications, control, data mining, design, |
||
| + | combinatorial optimization, power systems, signal processing, and many others. |
||
| + | To date, there are hundreds of publications reporting applications of particle |
||
| + | swarm optimization algorithms. For a review, see (Poli 2008). Although PSO has |
||
| + | been used mainly to solve unconstrained, single-objective optimization problems, PSO algorithms |
||
| + | have been developed to solve constrained problems, multi-objective |
||
| + | optimization problems, problems with dynamically changing landscapes, and to |
||
| + | find multiple solutions. For a review, see (Engelbrecht 2005). |
||
| + | A number of research directions are currently pursued, including: |
||
| − | Particle swarm optimization algorithms have been applied in many domains, including neural networks (the first application of these algorithms), telecommunications, data mining, combinatorial optimization, power systems, signal processing, and many others. There are hundreds of publications |
||
| + | *Theoretical aspects |
||
| − | reporting applications of particle swarm optimization algorithms. For a review, please see~\cite{Poli08a}. |
||
| + | *Matching algorithms (or algorithmic components) to problems |
||
| − | |||
| + | *Application to more and/or different kind of problems (e.g., multiobjective) |
||
| − | === Multiobjective PSO === |
||
| + | *Parameter selection |
||
| − | |||
| + | *Comparisons between PSO variants and other algorithms |
||
| − | The particle swarm optimization algorithm has also been adapted to tackle {\bf multiobjective optimization problems}~\cite{Reyes06}. |
||
| + | *New variants |
||
| − | The main differences between traditional single-objective particle swarm optimization algorithms and their multiobjective counterparts |
||
| − | are: |
||
| − | * Leader selection. In multiobjective optimization problems there is no single best solution that dominates all the others. The challenge, therefore, is to select from among equally good solutions one that can guide a particle toward the true Pareto front of the problem. |
||
| − | |||
| − | * Output set generation. The output of a multiobjective optimizer is the set of nondominated solutions found during the whole run of the algorithm. The common approach used in multiobjective particle swarm optimization algorithms is to maintain a ''solution archive'' in which the set of nondominated solutions are stored. |
||
| − | |||
| − | * Diversity mechanisms. To find diverse solutions that spread across the problem's Pareto front, multiobjective optimization algorithms must maintain a high level of diversity so as to avoid convergence to a single solution. In multiobjective particle swarm optimizers an extra mutation operator is usually added for this purpose. |
||
| − | |||
| − | |||
| − | == Current Research Issues == |
||
| − | |||
| − | Current research in particle swarm optimization is done along several lines. Some of them are: |
||
| − | |||
| − | \begin{description} |
||
| − | \item[Theory.] Understanding how particle swarm optimizers work, from a theoretical point of view, has been the subject of active |
||
| − | research in the last years. The first efforts were directed toward understanding the effects of the different parameters in the |
||
| − | behavior of the standard particle swarm optimization algorithm~\cite{Ozcan99,Clerc02,Trelea03}. In recent years there |
||
| − | has been a particular interest in studying the stochastic properties of the pair of stochastic equations that govern the movement of a particle~\cite{Blackwell07,Poli08b,Pena08}. |
||
| − | |||
| − | |||
| − | \item[New variants.] This line of research has been the most active since the proposal of the first particle swarm algorithm. |
||
| − | New particle position-update mechanisms are continuously proposed in an effort to design ever better performing particle swarms. |
||
| − | Some efforts are directed toward understanding on which classes of problems particular particle swarm algorithms can be top |
||
| − | performers~\cite{Poli05a,Poli05b,Langdon07}. Also of interest is the study of hybridizations between particle swarms and other |
||
| − | high-performing optimization algorithms~\cite{Lovbjerg01,Naka03}. Recently, some parallel implementations have been studied~\cite{Schutte04,Koh06} |
||
| − | and due to the wider availability of parallel computers, we should expect more research to be done along this line. |
||
| − | |||
| − | \item[Performance evaluation.] Due to the great number of new variants that are frequently proposed, performance comparisons have been always |
||
| − | of interest. Comparisons between the standard particle swarm and other optimization techniques, like the ones in ~\cite{Eberhart98,Hassan05}, |
||
| − | have triggered the interest of many researchers on particle swarm optimization. Comparisons between different particle |
||
| − | swarm optimization variants or empirical parameter settings studies help in improving our understanding of the technique and |
||
| − | many times trigger empirical and theoretical work~\cite{Mendes04,Schutte05,MdeO06}. |
||
| − | |||
| − | \item[Applications.] It is expected that in the future more applications of the particle swarm optimization algorithm will be considered. |
||
| − | Much of the work done on other aspects of the paradigm will hopefully allow us to solve practically relevant problems in many domains. |
||
| − | |||
| − | \end{description} |
||
==Notes== |
==Notes== |
||
| + | <math>^1</math>Without loss of generality, the presentation considers only minimization problems. |
||
| − | <references /> |
||
== References == |
== References == |
||
| − | |||
| − | M. Clerc. Discrete particle swarm optimization, illustrated by the traveling salesman problem. In ''New Optimization Techniques in Engineering'', pages 219-239. Springer, Berlin, Germany, 2004. |
||
M. Clerc. ''Particle Swarm Optimization''. ISTE, London, UK, 2006. |
M. Clerc. ''Particle Swarm Optimization''. ISTE, London, UK, 2006. |
||
| + | |||
| + | M. Clerc and J. Kennedy. The particle swarm-explosion, stability and |
||
| + | convergence in a multidimensional complex space. ''IEEE Transactions on Evolutionary Computation'', 6(1):58-73, 2002. |
||
A. P. Engelbrecht. ''Fundamentals of Computational Swarm Intelligence''. John Wiley & Sons, Chichester, UK, 2005. |
A. P. Engelbrecht. ''Fundamentals of Computational Swarm Intelligence''. John Wiley & Sons, Chichester, UK, 2005. |
||
| + | F. Heppner and U. Grenander. A stochastic nonlinear model for coordinated bird |
||
| − | Y. Fukuyama, S. Takayama, Y. Nakanishi, and H. Yoshida. A particle swarm optimization for reactive power and voltage control in electric power systems. In ''Proceedings of the Genetic and Evolutionary Computation Conference'', pages 1523-1528, Morgan Kaufmann, San Francisco,CA, 1999. |
||
| + | flocks. ''The Ubiquity of Chaos''. AAAS Publications, Washington, DC, 1990. |
||
| − | |||
| − | F. Heppner and U. Grenander. A stochastic nonlinear model for coordinated bird fl |
||
| − | ocks. ''The Ubiquity of Chaos''. AAAS Publications, Washington, DC, 1990. |
||
J. Kennedy. Bare bones particle swarms. In ''Proceedings of the IEEE Swarm Intelligence Symposium'', pages 80-87, IEEE Press, Piscataway, NJ, 2003. |
J. Kennedy. Bare bones particle swarms. In ''Proceedings of the IEEE Swarm Intelligence Symposium'', pages 80-87, IEEE Press, Piscataway, NJ, 2003. |
||
| + | |||
| + | J. Kennedy. Swarm Intelligence. In ''Handbook of Nature-Inspired and Innovative Computing: Integrating Classical Models with Emerging Technologies''. A. Y. Zomaya (Ed.) , pages 187-219, Springer US, Secaucus, NJ, 2006. |
||
J. Kennedy and R. Eberhart. Particle swarm optimization. In ''Proceedings of IEEE International Conference on Neural Networks'', pages 1942-1948, IEEE Press, Piscataway, NJ, 1995. |
J. Kennedy and R. Eberhart. Particle swarm optimization. In ''Proceedings of IEEE International Conference on Neural Networks'', pages 1942-1948, IEEE Press, Piscataway, NJ, 1995. |
||
| − | J. Kennedy and R. Eberhart. A discrete binary version of the particle swarm |
+ | J. Kennedy and R. Eberhart. A discrete binary version of the particle swarm |
| + | algorithm. In ''Proceedings of the IEEE International Conference on Systems, Man and Cybernetics'', pages 4104-4108, IEEE Press, Piscataway, NJ, 1997. |
||
J. Kennedy, and R. Eberhart. ''Swarm Intelligence''. Morgan Kaufmann, San Francisco, CA, 2001. |
J. Kennedy, and R. Eberhart. ''Swarm Intelligence''. Morgan Kaufmann, San Francisco, CA, 2001. |
||
| + | R. Mendes, J. Kennedy, and J. Neves. The fully informed particle swarm: |
||
| − | E. C. Laskari, K. E. Parsopoulos, and M. N. Vrahatis. Particle swarm optimization for integer programming. In ''Proceedings of the IEEE Congress on Evolutionary Computation'', pages 1582-1587, IEEE Press, Piscataway, NJ, 2002. |
||
| + | simpler, maybe better. ''IEEE Transactions on Evolutionary Computation'', 8(3):204-210, 2004. |
||
| − | + | A. Nowak, J. Szamrej, and B. Latané. From Private Attitude to Public Opinion: A Dynamic Theory of Social Impact. ''Psychological Review'', 97(3):362-376, 1990. |
|
| + | R. Poli. Analysis of the publications on the applications of particle swarm |
||
| − | R. Poli, J. Kennedy, and T. Blackwell. Particle swarm optimization. An overview. ''Swarm Intelligence'', 1(1):33-57, 2007. |
||
| + | optimisation. ''Journal of Artificial Evolution and Applications'', Article ID 685175, 10 pages, 2008. |
||
| + | R. Poli, J. Kennedy, and T. Blackwell. Particle swarm optimization. An |
||
| − | W. T. Reeves. Particle systems-a technique for modeling a class of fuzzy objects. ''ACM Transactions on Graphics'', 2(2):91-108, 1983. |
||
| + | overview. ''Swarm Intelligence'', 1(1):33-57, 2007. |
||
| + | W. T. Reeves. Particle systems--A technique for modeling a class of fuzzy |
||
| − | T. J. Richer and T. M. Blackwell. The Lévy Particle Swarm. In ''Proceedings of the IEEE Congress on Evolutionary Computation'', pages 808-815, IEEE Press, Piscataway, NJ, 2006. |
||
| + | objects. ''ACM Transactions on Graphics'', 2(2):91-108, 1983. |
||
C. W. Reynolds. Flocks, herds, and schools: A distributed behavioral model. ''ACM Computer Graphics'',21(4):25-34, 1987. |
C. W. Reynolds. Flocks, herds, and schools: A distributed behavioral model. ''ACM Computer Graphics'',21(4):25-34, 1987. |
||
== External Links == |
== External Links == |
||
| + | * Papers on PSO are published regularly in many journals and conferences: |
||
| − | * Many journals and conferences publish papers on PSO: |
||
| + | ** [http://www.springer.com/11721 Swarm Intelligence] (the main journal reporting on swarm intelligence research) regularly publishes articles on PSO. Other journals also publish articles about PSO. These include the IEEE Transactions series, [http://www.elsevier.com/locate/asoc/ Applied Soft Computing], [http://www.springer.com/computer/foundations/journal/11047 Natural Computing], [http://www.springer.com/engineering/journal/158 Structural and Multidisciplinary Optimization], and others. |
||
| − | ** The main journal reporting research on PSO is [http://www.springer.com/11721 Swarm Intelligence]. Other journals where papers on PSO regularly appear are IEEE Transactions on Evolutionary Computation, etc. |
||
| + | ** [http://iridia.ulb.ac.be/~ants ''ANTS - International Conference on Swarm Intelligence''], started in 1998. |
||
| − | ** GECCO, ANTS, IEEE SIS, Evo\* |
||
| + | ** [http://www.computelligence.org/sis ''The IEEE Swarm Intelligence Symposia''], started in 2003. |
||
| + | ** Special sessions or special tracks on PSO are organized in many conferences. Examples are the IEEE Congress on Evolutionary Computation (CEC) and the Genetic and Evolutionary Computation (GECCO) series of conferences. |
||
| + | ** Papers on PSO are also published in the proceedings of many other conferences such as Parallel Problem Solving from Nature conferences, the European Workshops on the Applications of Evolutionary Computation and many others. |
||
| + | |||
== See also == |
== See also == |
||
| − | [[ |
+ | [[Swarm Intelligence]], [[Ant Colony Optimization]], [[Optimization]], [[Stochastic Optimization]] |
[[Category: Computational Intelligence]] |
[[Category: Computational Intelligence]] |
||
Latest revision as of 17:51, 7 November 2008
Particle swarm optimization (PSO) is a population-based stochastic approach for solving continuous and discrete optimization problems.
In particle swarm optimization, simple software agents, called particles, move in the solution space of an optimization problem. The position of a particle represents a candidate solution to the optimization problem at hand. Particles search for better positions in the solution space by changing their velocity according to rules originally inspired by behavioral models of bird flocking.
Particle swarm optimization belongs to the class of swarm intelligence techniques that are used to solve optimization problems.
History
Particle swarm optimization was introduced by Kennedy and Eberhart (1995). It has roots in the simulation of social behaviors using tools and ideas taken from computer graphics and social psychology research.
Within the field of computer graphics, the first antecedents of particle swarm optimization can be traced back to the work of Reeves (1983), who proposed particle systems to model objects that are dynamic and cannot be easily represented by polygons or surfaces. Examples of such objects are fire, smoke, water and clouds. In these models, particles are independent of each other and their movement is governed by a set of rules. Some years later, Reynolds (1987) used a particle system to simulate the collective behavior of a flock of birds. In a similar kind of simulation, Heppner and Grenander (1990) included a roost that was attractive to the simulated birds. Both models inspired the set of rules that were later used in the original particle swarm optimization algorithm.
Social psychology research, in particular the dynamic theory of social impact (Nowak, Szamrej & Latané, 1990), was another source of inspiration in the development of the first particle swarm optimization algorithm (Kennedy, 2006). The rules that govern the movement of the particles in a problem's solution space can also be seen as a model of human social behavior in which individuals adjust their beliefs and attitudes to conform with those of their peers (Kennedy & Eberhart 1995).
Standard PSO algorithm
Preliminaries
The problem of minimizing<math>^1</math> the function <math>f: \Theta \to \mathbb{R}</math> with <math>\Theta \subseteq \mathbb{R}^n</math> can be stated as finding the set
<math>\Theta^* = \underset{\vec{\theta} \in \Theta}{\operatorname{arg\,min}} \, f(\vec{\theta}) = \{ \vec{\theta}^* \in \Theta \colon f(\vec{\theta}^*) \leq f(\vec{\theta}), \,\,\,\,\,\,\forall \vec{\theta} \in \Theta\}\,,</math>
where <math>\vec{\theta}</math> is an <math>n</math>-dimensional vector that belongs to the set of feasible solutions <math>\Theta</math> (also called solution space).
In PSO, the so-called swarm is composed of a set of particles <math>\mathcal{P} = \{p_{1},p_{2},\ldots,p_{k}\}</math>. A particle's position represents a candidate solution of the considered optimization problem represented by an objective function <math>f</math>. At any time step <math>t</math>, <math>p_i</math> has a position <math>\vec{x}^{\,t}_i</math> and a velocity <math>\vec{v}^{\,t}_i</math> associated to it. The best position that particle <math>p_i</math> (with respect to <math>f</math>) has ever visited until time step <math>t</math> is represented by vector <math>\vec{b}^{\,t}_i</math> (also known as a particle's personal best). Moreover, a particle <math>p_i</math> receives information from its neighborhood <math>\mathcal{N}_i \subseteq \mathcal{P}</math>. In the standard particle swarm optimization algorithm, the particles' neighborhood relations are commonly represented as a graph <math>G=\{V,E\}</math>, where each vertex in <math>V</math> corresponds to a particle in the swarm and each edge in <math>E</math> establishes a neighbor relation between a pair of particles. The resulting graph is commonly referred to as the swarm's population topology (Figure 1).
The algorithm
The PSO algorithm starts with the random generation of the particles' positions within an initialization region <math>\Theta^\prime \subseteq \Theta</math>. Velocities are usually initialized within <math>\Theta^\prime</math> but they can also be initialized to zero or to small random values to prevent them leaving the search space during the first iterations. During the main loop of the algorithm, the particles' velocities and positions are iteratively updated until a stopping criterion is met.
The update rules are:
<math>\vec{v}^{\,t+1}_i = w\vec{v}^{\,t}_i + \varphi_2\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i) \,,</math>
<math>\vec{x}^{\,t+1}_i = \vec{x}^{\,t}_i +\vec{v}^{\,t+1}_i \,,</math>
where <math>w</math> is a parameter called inertia weight, <math>\varphi_1</math> and <math>\varphi_2</math> are two parameters called acceleration coefficients, <math>\vec{U}^{\,t}_1</math> and <math>\vec{U}^{\,t}_2</math> are two <math>n \times n</math> diagonal matrices in which the entries in the main diagonal are distributed in the interval <math>[0,1)\,</math> uniformly at random. At every iteration, these matrices are regenerated. Usually, vector <math>\vec{l}^{\,t}_i</math>, referred to as the neighborhood best, is the best position ever found by any particle in the neighborhood of particle <math>p_i</math>, that is, <math>f(\vec{l}^{\,t}_i) \leq f(\vec{b}^{\,t}_j) \,\,\, \forall p_j \in \mathcal{N}_i</math>. If the values of <math>w</math>, <math>\varphi_1</math> and <math>\varphi_2</math> are properly chosen, it is guaranteed that the particles' velocities do not grow to infinity (Clerc and Kennedy 2002).
The three terms in the velocity update rule characterize the local behaviors that particles follow. The first term, called the inertia or momentum serves as a memory of the previous flight direction, preventing the particle from drastically changing direction. The second term, called the cognitive component resembles the tendency of particles to return to previously found best positions. The third term, called the social component quantifies the performance of a particle relative to its neighbors. It represents a group norm or standard that should be attained.
In some cases, particles can be attracted to regions outside the feasible search space <math>\Theta</math>. For this reason, mechanisms for preserving solution feasibility and a proper swarm operation have been devised (Engelbrecht 2005). One of the least disruptive mechanisms for handling constraints is one in which particles going outside <math>\Theta</math> are not allowed to improve their personal best position so that they are attracted back to the feasible space in subsequent iterations.
A pseudocode version of the standard PSO algorithm is shown below:
:Inputs Objective function <math>f:\Theta \to \mathbb{R}</math>, the initialization domain <math>\Theta^\prime \subseteq \Theta</math>,
the number of particles <math>|\mathcal{P}| = k</math>, the parameters <math>w</math>, <math>\varphi_1</math>, and <math>\varphi_2</math>, and the stopping criterion <math>S</math>
:Output Best solution found
// Initialization
Set t := 0
for i := 1 to k do
Initialize <math>\mathcal{N}_i</math> to a subset of <math>\mathcal{P}</math> according to the desired topology
Initialize <math>\vec{x}^{\,t}_i</math> randomly within <math>\Theta^\prime</math>
Initialize <math>\vec{v}^{\,t}_i</math> to zero or a small random value
Set <math>\vec{b}^{\,t}_i = \vec{x}^{\,t}_i</math>
end for
// Main loop
while <math>S</math> is not satisfied do
// Velocity and position update loop
for i := 1 to k do
Set <math>\vec{l}^{\,t}_i</math> := <math>\underset{{\vec{b}^{\,t}}_j \in \Theta \,|\, p_j \in \mathcal{N}_i}{\operatorname{arg\,min}} \, f({\vec{b}^{\,t}}_j)</math>
Generate random matrices <math>\vec{U}^{\,t}_1</math> and <math>\vec{U}^{\,t}_2</math>
Set <math>\vec{v}^{\,t+1}_i</math> := <math>w\vec{v}^{\,t}_i + \varphi_1\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i)</math>
Set <math>\vec{x}^{\,t+1}_i</math> := <math>\vec{x}^{\,t}_i + \vec{v}^{\,t+1}_i</math>
end for
// Solution update loop
for i := 1 to k do
if <math>f(\vec{x}^{\,t}_i) < f(\vec{b}^{\,t}_i)</math>
Set <math>\vec{b}^{\,t}_i</math> := <math>\vec{x}^{\,t}_i</math>
end if
end for
Set t := t + 1
end while
The algorithm above follows synchronous updates of particle positions and best positions, where the best position found is updated only after all particle positions and personal best positions have been updated. In asynchronous update mode, the best position found is updated immediately after each particle's position update. Asynchronous updates have a faster propagation of best solutions through the swarm.
Main PSO variants
The original particle swarm optimization algorithm has undergone a number of changes since it was first proposed. Most of these changes affect the way the particles' velocity is updated. In the following subsections, we briefly describe some of the most important developments. For a more detailed description of many of the existing particle swarm optimization variants, see (Kennedy and Eberhart 2001, Engelbrecht 2005, Clerc 2006 and Poli et al. 2007).
Discrete PSO
Most particle swarm optimization algorithms are designed to search in continuous domains. However, there are a number of variants that operate in discrete spaces. The first variant that worked on discrete domains was the binary particle swarm optimization algorithm (Kennedy and Eberhart 1997). In this algorithm, a particle's position is discrete but its velocity is continuous. The <math>j</math>th component of a particle's velocity vector is used to compute the probability with which the <math>j</math>th component of the particle's position vector takes a value of 1. Velocities are updated as in the standard PSO algorithm, but positions are updated using the following rule:
<math> x^{t+1}_{ij} = \begin{cases} 1 & \mbox{if } r < sig(v^{t+1}_{ij}),\\ 0 & \mbox{otherwise,} \end{cases} </math>
where <math>x_{ij}</math> is the <math>j</math>th component of the position vector of particle <math>p_i</math>, <math>r</math> is a uniformly distributed random number in the range <math>[0,1)\,</math> and
<math> sig(x) = \frac{1}{1+e^{-x}}\,. </math>
Constriction Coefficient
The constriction coefficient was introduced as an outcome of a theoretical analysis of swarm dynamics (Clerc and Kennedy 2002). Velocities are constricted, with the following change in the velocity update: <math>\vec{v}^{\,t+1}_i = \chi^t[\vec{v}^{\,t}_i + \varphi_2\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i)]</math> where <math>\chi^t</math> is an <math>n \times n</math> diagonal matrix in which the entries in the main diagonal are calculated as
<math>\chi^t_{jj}=\frac{2\kappa}{|2-\varphi^t_{jj}-\sqrt{\varphi^t_{jj}(\varphi^t_{jj}-2)}|}</math> with <math>\varphi^t_{jj}=\varphi_1U^t_{1,jj}+\varphi_2U^t_{2,jj}</math>. Convergence is guaranteed under the conditions that <math>\varphi^t_{jj}\ge 4\,\forall j</math> and <math>\kappa\in [0,1]</math>.
Bare-bones PSO
The bare-bones particle swarm (Kennedy 2003) is a variant of the particle swarm optimization algorithm in which the velocity- and position-update rules are substituted by a procedure that samples a parametric probability density function.
In the bare-bones particle swarm optimization algorithm, a particle's position update rule in the <math>j</math>th dimension is <math> x^{t+1}_{ij} = N\left(\mu_{ij}^{t} ,\sigma_{ij}^{\,t}\right)\,, </math> where <math>N</math> is a normal distribution with
<math> \begin{array}{ccc} \mu_{ij}^{t} &=& \frac{b^{t}_{ij} + l^{t}_{ij}}{2} \,, \\ \sigma_{ij}^{t} & = & |b^{t}_{ij} - l^{t}_{ij}| \,. \end{array} </math>
Fully informed PSO
In the standard particle swarm optimization algorithm, a particle is attracted toward its best neighbor. A variant in which a particle uses the information provided by all its neighbors in order to update its velocity is called the fully informed particle swarm (FIPS) (Mendes et al. 2004).
In the fully informed particle swarm optimization algorithm, the velocity-update rule is
<math> \vec{v}^{\,t+1}_i = w\vec{v}^{\,t}_i + \frac{\varphi}{|\mathcal{N}_i|}\sum_{p_j \in \mathcal{N}_i}\mathcal{W}(\vec{b}^{\,t}_j)\vec{U}^{\,t}_j(\vec{b}^{\,t}_j-\vec{x}^{\,t}_i) \,, </math> where <math>\mathcal{W} \colon \Theta \to [0,1]</math> is a function that weighs the contribution of a particle's personal best position to the movement of the target particle based on its relative quality.
Applications of PSO and Current Trends
The first practical application of a PSO algorithm was in the field of neural network training and was published together with the algorithm itself (Kennedy and Eberhart 1995). Many more areas of application have been explored ever since, including telecommunications, control, data mining, design, combinatorial optimization, power systems, signal processing, and many others. To date, there are hundreds of publications reporting applications of particle swarm optimization algorithms. For a review, see (Poli 2008). Although PSO has been used mainly to solve unconstrained, single-objective optimization problems, PSO algorithms have been developed to solve constrained problems, multi-objective optimization problems, problems with dynamically changing landscapes, and to find multiple solutions. For a review, see (Engelbrecht 2005).
A number of research directions are currently pursued, including:
- Theoretical aspects
- Matching algorithms (or algorithmic components) to problems
- Application to more and/or different kind of problems (e.g., multiobjective)
- Parameter selection
- Comparisons between PSO variants and other algorithms
- New variants
Notes
<math>^1</math>Without loss of generality, the presentation considers only minimization problems.
References
M. Clerc. Particle Swarm Optimization. ISTE, London, UK, 2006.
M. Clerc and J. Kennedy. The particle swarm-explosion, stability and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation, 6(1):58-73, 2002.
A. P. Engelbrecht. Fundamentals of Computational Swarm Intelligence. John Wiley & Sons, Chichester, UK, 2005.
F. Heppner and U. Grenander. A stochastic nonlinear model for coordinated bird flocks. The Ubiquity of Chaos. AAAS Publications, Washington, DC, 1990.
J. Kennedy. Bare bones particle swarms. In Proceedings of the IEEE Swarm Intelligence Symposium, pages 80-87, IEEE Press, Piscataway, NJ, 2003.
J. Kennedy. Swarm Intelligence. In Handbook of Nature-Inspired and Innovative Computing: Integrating Classical Models with Emerging Technologies. A. Y. Zomaya (Ed.) , pages 187-219, Springer US, Secaucus, NJ, 2006.
J. Kennedy and R. Eberhart. Particle swarm optimization. In Proceedings of IEEE International Conference on Neural Networks, pages 1942-1948, IEEE Press, Piscataway, NJ, 1995.
J. Kennedy and R. Eberhart. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, pages 4104-4108, IEEE Press, Piscataway, NJ, 1997.
J. Kennedy, and R. Eberhart. Swarm Intelligence. Morgan Kaufmann, San Francisco, CA, 2001.
R. Mendes, J. Kennedy, and J. Neves. The fully informed particle swarm: simpler, maybe better. IEEE Transactions on Evolutionary Computation, 8(3):204-210, 2004.
A. Nowak, J. Szamrej, and B. Latané. From Private Attitude to Public Opinion: A Dynamic Theory of Social Impact. Psychological Review, 97(3):362-376, 1990.
R. Poli. Analysis of the publications on the applications of particle swarm optimisation. Journal of Artificial Evolution and Applications, Article ID 685175, 10 pages, 2008.
R. Poli, J. Kennedy, and T. Blackwell. Particle swarm optimization. An overview. Swarm Intelligence, 1(1):33-57, 2007.
W. T. Reeves. Particle systems--A technique for modeling a class of fuzzy objects. ACM Transactions on Graphics, 2(2):91-108, 1983.
C. W. Reynolds. Flocks, herds, and schools: A distributed behavioral model. ACM Computer Graphics,21(4):25-34, 1987.
External Links
- Papers on PSO are published regularly in many journals and conferences:
- Swarm Intelligence (the main journal reporting on swarm intelligence research) regularly publishes articles on PSO. Other journals also publish articles about PSO. These include the IEEE Transactions series, Applied Soft Computing, Natural Computing, Structural and Multidisciplinary Optimization, and others.
- ANTS - International Conference on Swarm Intelligence, started in 1998.
- The IEEE Swarm Intelligence Symposia, started in 2003.
- Special sessions or special tracks on PSO are organized in many conferences. Examples are the IEEE Congress on Evolutionary Computation (CEC) and the Genetic and Evolutionary Computation (GECCO) series of conferences.
- Papers on PSO are also published in the proceedings of many other conferences such as Parallel Problem Solving from Nature conferences, the European Workshops on the Applications of Evolutionary Computation and many others.
See also
Swarm Intelligence, Ant Colony Optimization, Optimization, Stochastic Optimization