Supporting material for the article:

Estimation-based Metaheuristics for the
Vechicle Routing Problem with Stochastic Demands and Customers

First generated: November 2009. Last update:July 2010

Table of Contents

Abstract
Algorithms
Tuning
Instances used for testing
Effectiveness of 2.5-opt-EEais
Effectiveness of ANOVA-Race
Comparison between estimation-based metaheuristics
Numerical values and statistical bounds

1. Abstract:

The vehicle routing problem with stochastic demands and customers (VRPSDC) requires finding the optimal route for a capacitated vehicle that delivers goods to a set of customers, where each customer has a probability of requiring being visited and has a stochastic demand. Besides the usual difficulty of finding the optimal solution in a large search space, the VRPSDC has a computationally expensive cost function. For large instances, evaluation of the cost function is a primary bottleneck for finding high quality solutions in a reasonable computation time. We tackle this issue by using an empirical estimation approach, where the solution cost is estimated by Monte Carlo simulation. Moreover, we use the recently developed state-of-the-art iterative improvement algorithm for the closely related probabilistic traveling salesman problem as an underlying local search algorithm inside metaheuristic algorithms for the VRPSDC. We present an experimental study of several estimation-based algorithms on a number of problem instances. We show that the proposed algorithms outperform the current best algorithm for the given problem. Among the estimation-based algorithms, we show that an ant colony optimization algorithm is particularly effective.

Keywords: Vehicle routing problem with stochastic demands and customers, Metaheuristics, Iterative Improvement Algorithm, Empirical Estimation

2. Algorithms:

TABUSTOCH: Analytical computation tabu search algorithm of Gendreau et al.
2.5-opt-EEais: The state-of-the-art estimation-based local search for the PTSP.
RRLS-AC: Analytical computation random restart local search with 2.5-opt-EEais local search.
RRLS-EE: Estimation-based random restart local search with 2.5-opt-EEais local search.
ILS-EE: Estimation-based iterated local search with 2.5-opt-EEais local search.
MAGX-EE: Estimation-based Memetic algorithm with 2.5-opt-EEais local search.
ACS-EE: Estimation-based ant colony system with 2.5-opt-EEais local search.

3. Tuning :

Experimental set	File
`Tuning instances`	Clustered instances of size 1000
`Parameter configutations`	A set of 10 parameter configurations for each algorithm on 1000 CPU seconds

4. Instances used for testing :

Experimental set	File
`Instances used in Section 4.2`	Section4.2.tar.gz
`Instances used in Section 4.3`	Section4.3.tar.gz
`Instances used in Section 4.4`	Section4.4.tar.gz

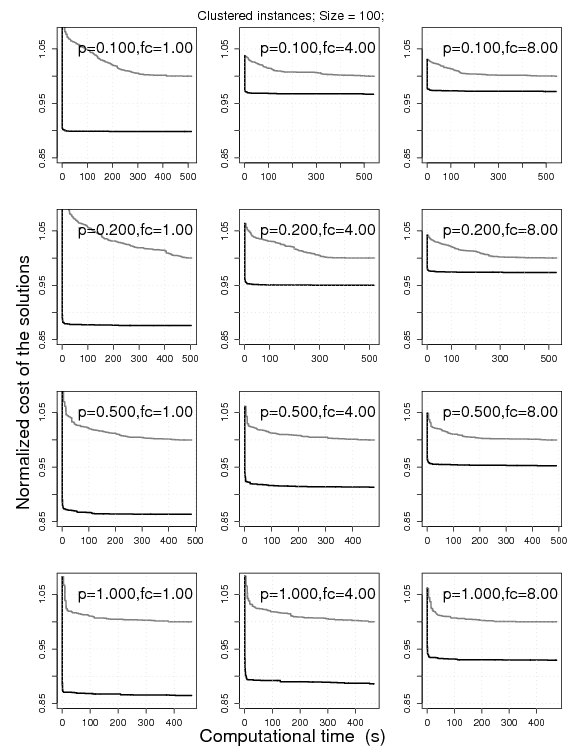
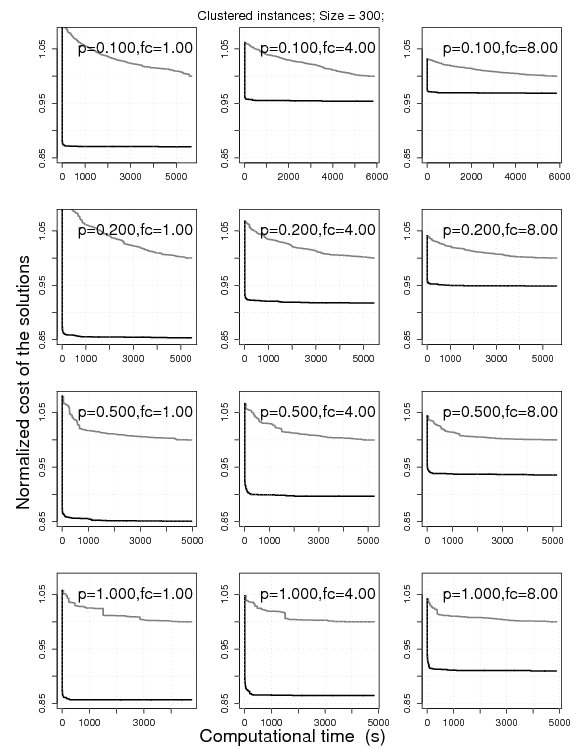
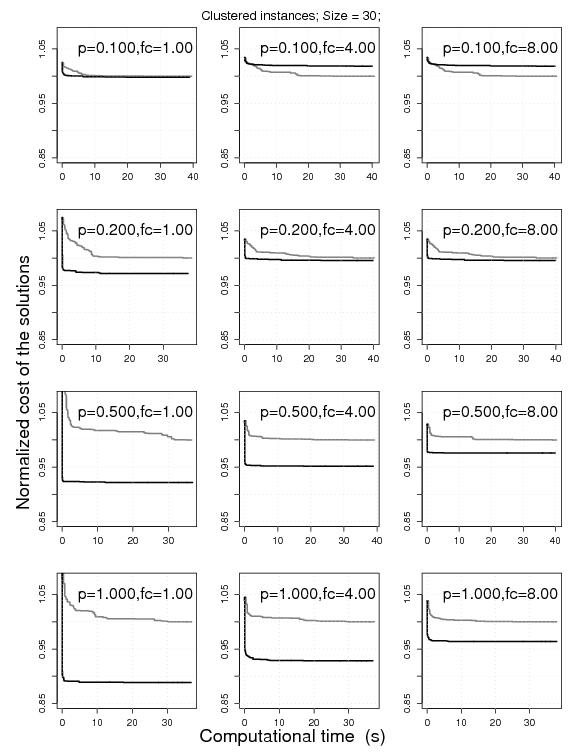
5. Effectiveness of 2.5-opt-EEais

Experimental results on the clustered VRPSDC instances of size 100. The plots represent the cost of the solutions obtained by RRLS-AC normalized by those obtained by TABUSTOCH. The normalization is done on an instance-by-instance basis for 10 instances; the normalized solution cost is then aggregated.

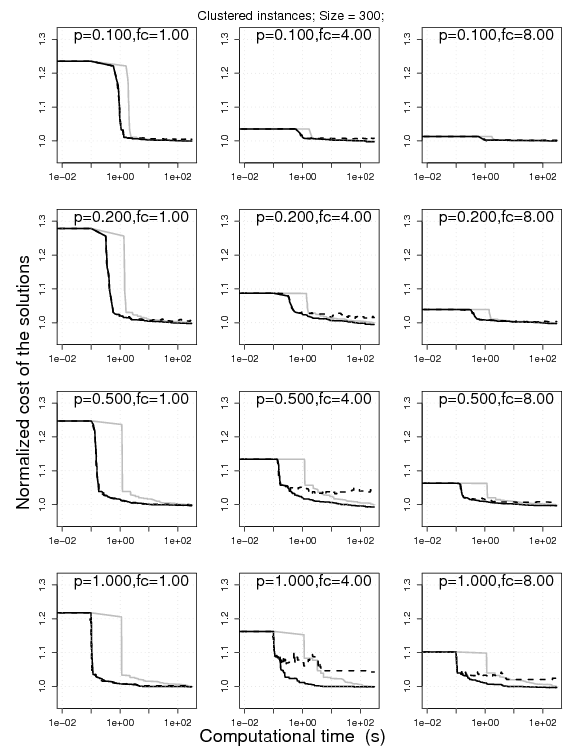
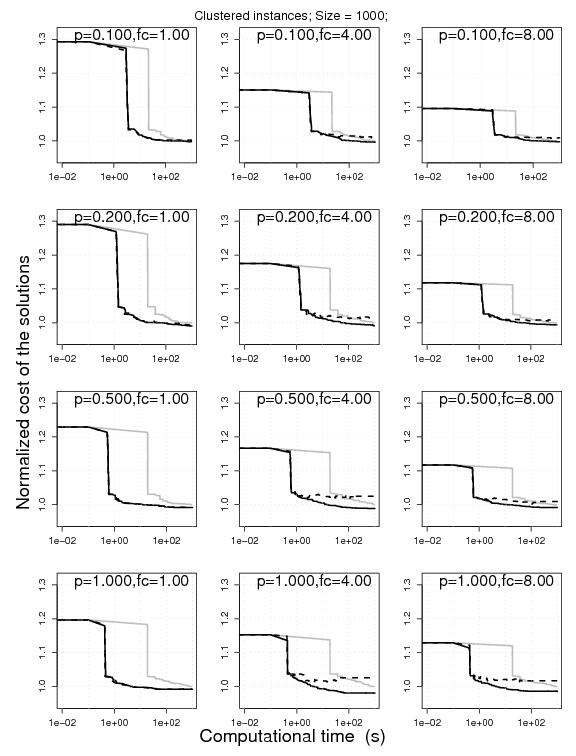
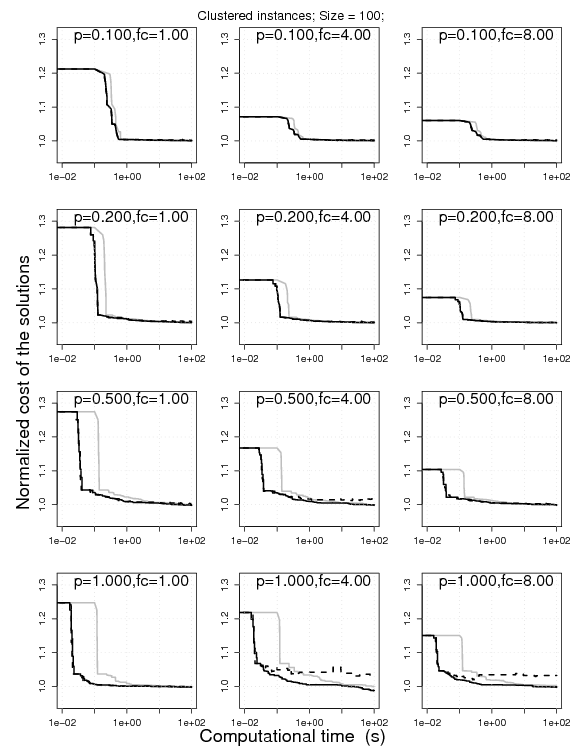
6. Effectiveness of ANOVA-Race

Experimental results on clustered VRPSDC instances of size of size 100, 300, 1000 under 100, 300, 1000 CPU seconds, respectively. The plots represent the cost of the solutions obtained by RRLS-EE, RRLS-EE(PTSP) normalized by the one obtained by RRLS-AC. The normalization is done on an instance-by-instance basis for 10 instances; the normalized solution cost is then aggregated.

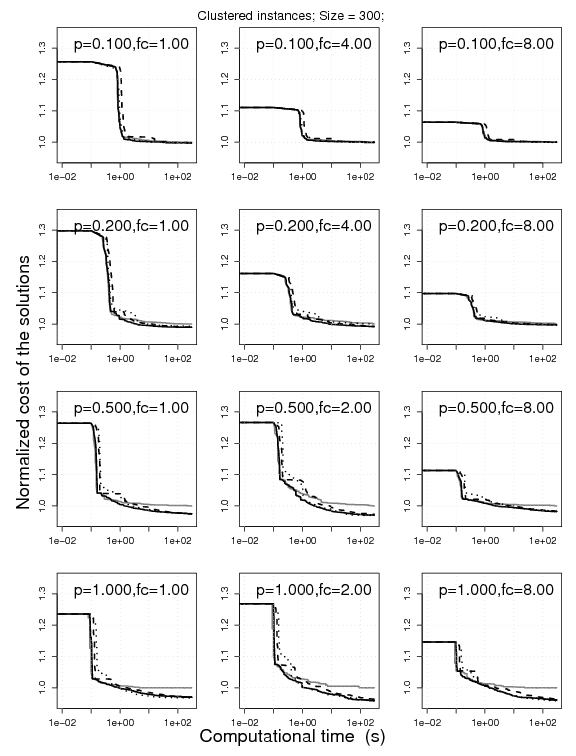
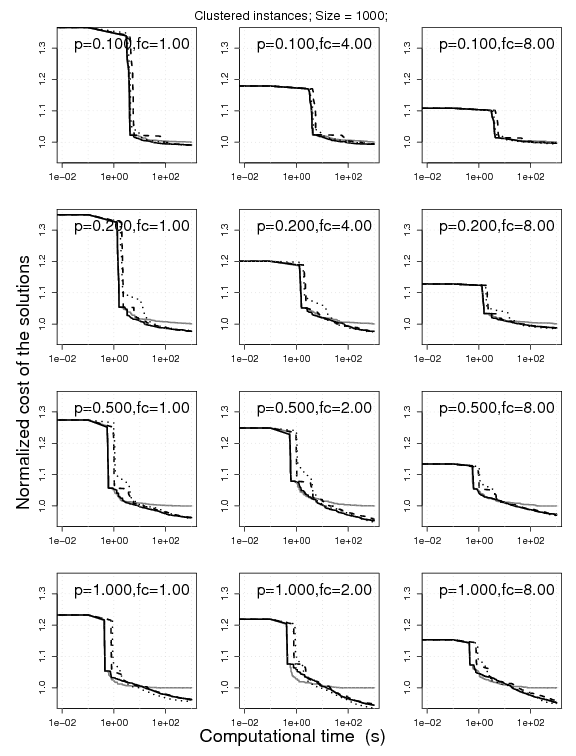
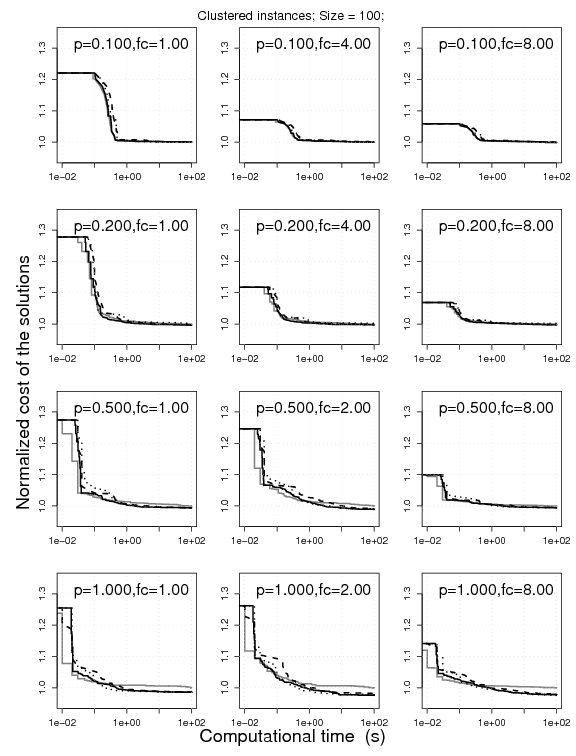
7. Comparison between estimation-based metaheuristics

Experimental results on clustered VRPSDC instances of size 100, 300, 1000 under 100, 300, 1000 CPU seconds, respectively. The plots represent the cost of the solutions obtained by ILS-EE, MAGX-EE, and ACS-EE normalized by the one obtained by RRLS-EE. The normalization is done on a instance-by-instance basis for 10 instances; the normalized solution cost is then aggregated.

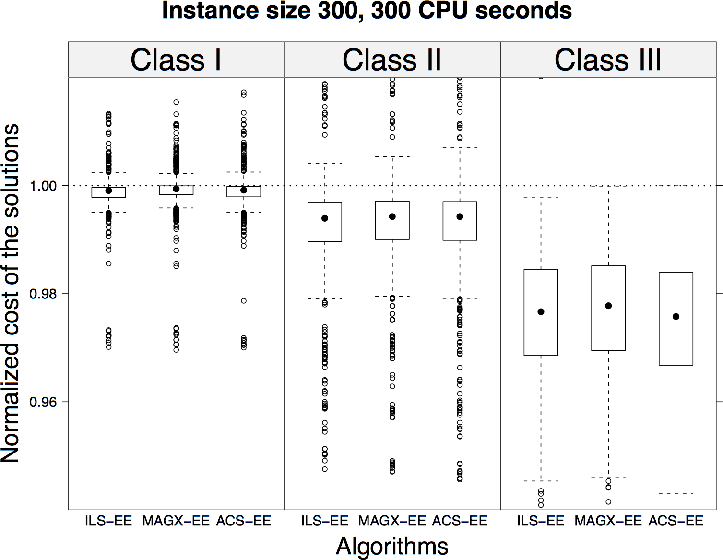
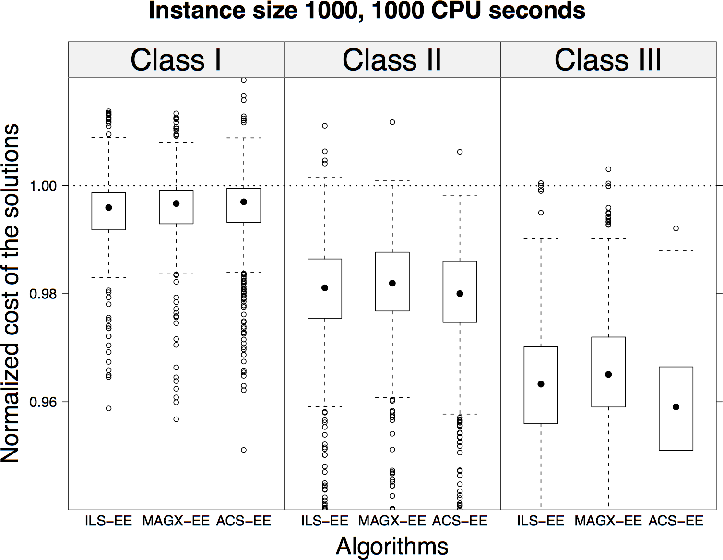
Experimental results on clustered VRPSDC instances. The box plots represent the cost of the solutions obtained by ILS-EE, MAGX-EE, and ACS-EE. The obtained solution costs of the algorithms are normalized by the final solution cost reached by RRLSEE. The normalization is done on an instance-by-instance basis for 10 instances; the normalized solution cost is then aggregated. The dotted horizontal line denotes therefore the final cost of RRLS-EE.

8. Numerical values and statistical results:

The absolute values for all the results in the form of tables. In these tables, we present the final solution quality and the corresponding computational time for each probabiltiy range. Moreover, in order to test that the observed difference between the cost of the solutions reached by the considered algorithms are significant in a statistical sense, we use a t test and we present the 95% confidence interval obtained from the t-test. The results are composed in a single pdf file:

Format
`PDF`	(click the above icon to see/download the results)