Self-Organised Recruitment and Deployment with Aerial and Ground-Based Robotic Swarms

Submitted to AAMAS 2010, Tracking Number: #528

[ Abstract ] [ Video ] [ Contact ]

  Abstract

We tackle the problem of dynamically forming and deploying groups of robots in a dynamic task allocation scenario. In our approach, wheeled robots carry out tasks and flying robots coordinate the formation and subsequent deployment of groups of wheeled robots. Our recruitment system is based on simple probabilistic rules inspired by the aggregation behaviour of cockroaches under shelters. The system successfully forms stable groups of the desired size and copes with the dynamic addition and removal of either wheeled robots or tasks. The system includes a deadlock resolution mechanism that allows the system to continue functioning even when there are not enough wheeled robots to carry out all tasks simultaneously. As the robotic hardware is still under development, our experiments are conducted in a physically realistic embodied simulation environment.


  Video


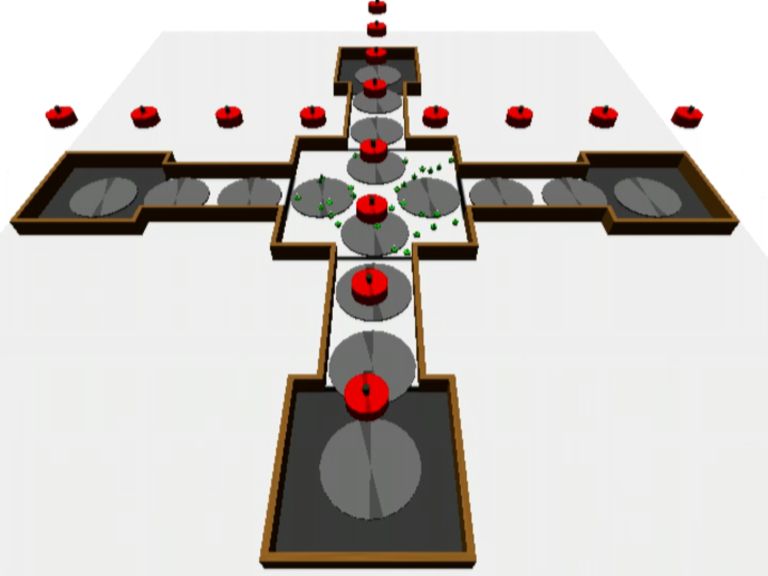
In this video, tasks are activated in sequence. An eye-bot requests 5 to 10 robots to execute the task it is coordinating. The request is relayed to the closest eye-bot in the recruitment area, which takes care of recruiting the needed foot-bots. When the team is formed, the recruiting eye-bot delivers it to the requesting eye-bot. After the execution of the task, the foot-bots are returned to the recruitment area. At this point, another eye-bot requests foot-bots for its task (9 to 13) and also in this case recruitment, delivery and return are successful. This is footage from one of the experimental trials described in our paper.

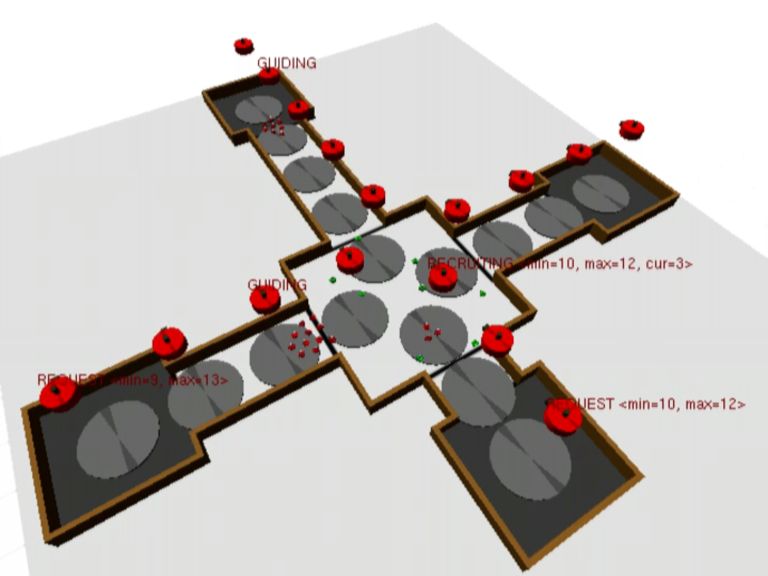
In this video, we show that the recruitment system is successful also when dealing with multiple parallel and asynchronous requests. Initially, two eye-bots request foot-bots at the same time. One eye-bot requests 5 to 10 foot-bots, the other 7 to 13. The requests are relayed to two eye-bots in the recruitment area. While the two foot-bot teams are formed in parallel, a third eye-bot requests 10 to 12 foot-bots. This new request triggers the redistribution of the already recruited foot-bots. Eventually, one team is formed and, when the team leaves the recruitment area, further redistribution takes place, thus allowing another group to be formed and sent to task execution. The third team is formed when the first is returned to the recruitment area. This is footage from one of the experimental trials described in our paper.

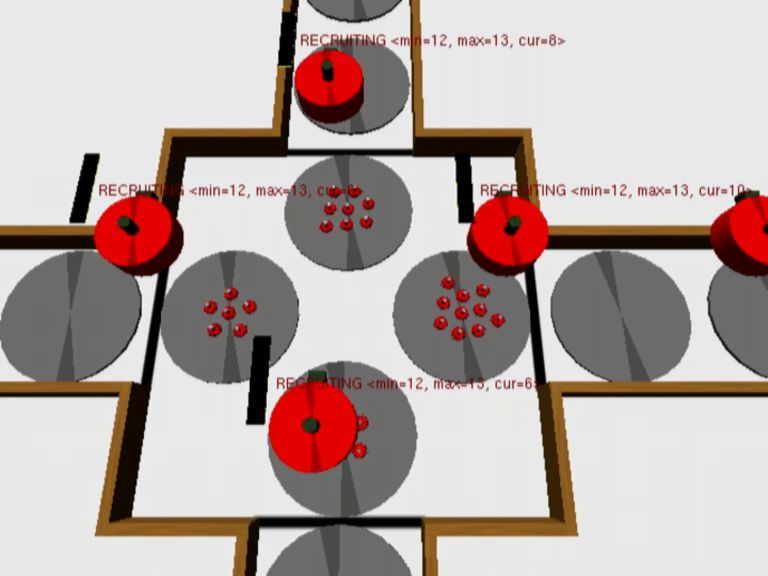
In this video, we show how deadlocks are solved in the system. There are 30 available foot-bots in the recruitment area and four simultaneous recruitment requests (min=12, max=13) are formulated at the same time. The eye-bots form their teams in parallel, but soon a deadlock happens -- no eye-bot can satisfy the minimum requested quota. When eye-bots detect convergence to a quota which is less than the minimum, it has a small probability to spike the leaving probability sent to the foot-bots. This simple mechanism is sufficient to allow the system to overcome the deadlock and continue functioning. This is footage from one of the experimental trials described in our paper.


  Contact

Webpages:

Swarm-bots: www.swarm-bots.org
Swarmanoid:www.swarmanoid.org

Address:

IRIDIA - ULB
50 Avenue F. Roosevelt - CP 194/9
1050 Bruxelles
Belgium