Difference between revisions of "Particle Swarm Optimization - Scholarpedia Draft"
| Line 21: | Line 21: | ||
the function <math>f: \Theta \to \mathbb{R}</math> with <math>\Theta \subseteq \mathbb{R}^n</math> can be stated as finding the set |
the function <math>f: \Theta \to \mathbb{R}</math> with <math>\Theta \subseteq \mathbb{R}^n</math> can be stated as finding the set |
||
| − | <math>\Theta^* = \ |
+ | <math>\Theta^* = \underset{\vec{\theta} \in \Theta}{\operatorname{arg\,min}} \, f(\vec{\theta}) = \{ \vec{\theta}^* \in \Theta \colon f(\vec{\theta}^*) \leq f(\vec{\theta}) \,\,\,\,\,\,\forall \vec{\theta} \in \Theta\}\,,</math> |
| − | where <math>\ |
+ | where <math>\vec{\theta}</math> is an <math>n</math>-dimensional vector that belongs to the set of feasible solutions <math>\Theta</math> (also called solution space). The elements of the set <math>\Theta^*</math> are equivalent with respect to the function <math>f</math>. |
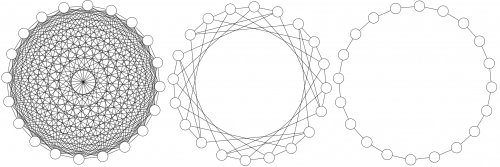
| − | [[Image:Topologies.png|thumb|500px|right|Example population topologies. The leftmost picture depicts a fully connected topology, that is, <math>{ |
+ | [[Image:Topologies.png|thumb|500px|right|Example population topologies. The leftmost picture depicts a fully connected topology, that is, <math>\mathcal{N}_i = \mathcal{P} \setminus \{p_i\}\,\,\forall p_i \in \mathcal{P}</math>. The picture in the center depicts a so-called von Neumann topology, in which <math>|\mathcal{N}_i| = 4\,\,\forall p_i \in \mathcal{P}</math>. The rightmost picture depicts a ring topology in which each particle is neighbor to two other particles.]] |
| − | Let <math> |
+ | Let <math>\mathcal{P} = \{p_{1},p_{2},\ldots,p_{k}\}</math> be the population of particles (also referred to as ''swarm''). |
| − | At any time step <math>t</math>, a particle <math>p_i</math> has a position <math>\ |
+ | At any time step <math>t</math>, a particle <math>p_i</math> has a position <math>\vec{x}^{\,t}_i</math> and a velocity <math>\vec{v}^{\,t}_i</math> associated to it. The best position that particle <math>p_i</math> has ever visited until time step <math>t</math> is represented by vector <math>\vec{b}^{\,t}_i</math> (also known as a particle's ''personal best''). Moreover, a particle <math>p_i</math> receives information from its ''neighborhood'', which is defined as the set <math>\mathcal{N}_i \subseteq \mathcal{P}</math>. Note that a particle can belong to its own neighborhood. In the standard particle swarm optimization algorithm, the particles' neighborhood relations are commonly represented as a graph <math>G=\{V,E\}</math>, where each vertex in <math>V</math> corresponds to a particle in the swarm and each edge in <math>E</math> establishes a neighbor relation between a pair of particles. The resulting graph is commonly referred to as the swarm's ''population topology''. |
=== The algorithm === |
=== The algorithm === |
||
| Line 36: | Line 36: | ||
The updating rules are: |
The updating rules are: |
||
| − | <math> |
||
| ⚫ | |||
| − | </math> |
||
| ⚫ | |||
| − | <math> |
||
| + | |||
| − | + | <math>\vec{x}^{\,t+1}_i = \vec{x}^{\,t}_i +\vec{v}^{\,t+1}_i \,,</math> |
|
| − | </math> |
||
| + | |||
| − | where <math>w</math> is a parameter called ''inertia weight'', <math>\varphi_1</math> and <math>\varphi_2</math> are two parameters called ''acceleration coefficients'', <math>\ |
+ | where <math>w</math> is a parameter called ''inertia weight'', <math>\varphi_1</math> and <math>\varphi_2</math> are two parameters called ''acceleration coefficients'', <math>\vec{U}^{\,t}_1</math> and <math>\vec{U}^{\,t}_2</math> are two <math>n \times n</math> diagonal matrices with in-diagonal elements distributed in the interval <math>[0,1)\,</math> uniformly at random. Every iteration, these matrices are regenerated, that is, <math>\vec{U}^{\,t+1}_{1,2} \neq \vec{U}^{\,t}_{1,2}</math>. Vector <math>\vec{l}^{\,t}_i</math> is the best position ever found by any particle in the neighborhood of particle <math>p_i</math>, that is, <math>f(\vec{l}^{\,t}_i) \leq f(\vec{b}^{\,t}_j) \,\,\, \forall p_j \in \mathcal{N}_i</math>. |
A pseudocode version of the standard PSO algorithm is shown below: |
A pseudocode version of the standard PSO algorithm is shown below: |
||
<code> |
<code> |
||
| − | :'''Inputs''' ''Objective function <math>f:\Theta \to \mathbb{R}</math>, the initialization domain <math>\Theta^\prime \subseteq \Theta</math>, the set of particles <math>{ |
+ | :'''Inputs''' ''Objective function <math>f:\Theta \to \mathbb{R}</math>, the initialization domain <math>\Theta^\prime \subseteq \Theta</math>, the set of particles <math>\mathcal{P} \colon |\mathcal{P}| = k</math>,'' |
| + | ''the parameters <math>w</math>, <math>\varphi_1</math>, and <math>\varphi_2</math>, and the stopping criterion <math>S</math>'' |
||
:'''Output''' ''Best solution found'' |
:'''Output''' ''Best solution found'' |
||
| Line 54: | Line 53: | ||
Set t := 0 |
Set t := 0 |
||
for i := 1 to k do |
for i := 1 to k do |
||
| − | Initialize <math>{ |
+ | Initialize <math>\mathcal{N}_i</math> to a subset of <math>\mathcal{P}</math> according to the desired topology |
Initialize <math>\vec{x}^{\,t}_i</math> and <math>\vec{v}^{\,t}_i</math> randomly within <math>\Theta^\prime</math> |
Initialize <math>\vec{x}^{\,t}_i</math> and <math>\vec{v}^{\,t}_i</math> randomly within <math>\Theta^\prime</math> |
||
Set <math>\vec{b}^{\,t}_i = \vec{x}^{\,t}_i</math> |
Set <math>\vec{b}^{\,t}_i = \vec{x}^{\,t}_i</math> |
||
| Line 65: | Line 64: | ||
for i := 1 to k do |
for i := 1 to k do |
||
Set <math>\vec{l}^{\,t}_i</math> := <math>p_i</math>'s best neighbor according to <math>f</math> |
Set <math>\vec{l}^{\,t}_i</math> := <math>p_i</math>'s best neighbor according to <math>f</math> |
||
| − | Generate random |
+ | Generate random matrices <math>\vec{U}^{\,t}_1</math> and <math>\vec{U}^{\,t}_1</math> |
Set <math>\vec{v}^{\,t+1}_i</math> := <math>w\vec{v}^{\,t}_i + \varphi_1\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i)</math> |
Set <math>\vec{v}^{\,t+1}_i</math> := <math>w\vec{v}^{\,t}_i + \varphi_1\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i)</math> |
||
Set <math>\vec{x}^{\,t+1}_i</math> := <math>\vec{x}^{\,t}_i + \vec{v}^{\,t+1}_i</math> |
Set <math>\vec{x}^{\,t+1}_i</math> := <math>\vec{x}^{\,t}_i + \vec{v}^{\,t+1}_i</math> |
||
| Line 72: | Line 71: | ||
// Solution update loop |
// Solution update loop |
||
for i := 1 to k do |
for i := 1 to k do |
||
| − | if <math>f(\ |
+ | if <math>f(\vec{x}^{\,t}_i) \leq f(\vec{b}^{\,t}_i)</math> |
| − | Set <math>\ |
+ | Set <math>\vec{b}^{\,t}_i</math> := <math>\vec{x}^{\,t}_i</math> |
end if |
end if |
||
end for |
end for |
||
Revision as of 11:02, 1 October 2008
Particle swarm optimization (PSO) is a population-based stochastic approach for tackling continuous and discrete optimization problems.
In particle swarm optimization, simple software agents, called particles move in the solution space of an optimization problem. The position of a particle represents a candidate solution to the optimization problem at hand. Particles search for better positions in the solution space by changing their velocity according to rules originally inspired by behavioral models of bird flocking.
Particle swarm optimization belongs to the class of swarm intelligence techniques that are used solve optimization problems.
History
Particle swarm optimization was introduced by Kennedy and Eberhart (1995). It has roots in the simulation of social behaviors using tools and ideas taken from computer graphics and social psychology research.
Within the field of computer graphics, the first antecedents of particle swarm optimization can be traced back to the work of Reeves (1983), who proposed particle systems to model objects that are dynamic and cannot be easily represented by polygons or surfaces. Examples of such objects are fire, smoke, water and clouds. In these models, particles are independent of each other and their movement is governed by a set of rules. Some years later, Reynolds (1987) used a particle system to simulate the collective behavior of a flock of birds. In a similar kind of simulation, Heppner and Grenander (1990) included a "roost" that was attractive to the simulated birds. Both models inspired the set of rules that were later used in the original particle swarm optimization algorithm.
Social psychology research was another source of inspiration in the development of the first particle swarm optimization algorithm. The rules that govern the movement of the particles in a problem's solution space can also be seen as a model of social cognition in which successful individuals tend to be imitated by less successful ones (Kennedy & Eberhart 1995).
The name particle swarm was chosen because the collective behavior of the particles adheres to the principles described by Millonas (1994).
Standard PSO algorithm
Preliminaries
The problem of minimizing <ref name="minimization">Without loss of generality, the presentation considers only minimization problems.</ref> the function <math>f: \Theta \to \mathbb{R}</math> with <math>\Theta \subseteq \mathbb{R}^n</math> can be stated as finding the set
<math>\Theta^* = \underset{\vec{\theta} \in \Theta}{\operatorname{arg\,min}} \, f(\vec{\theta}) = \{ \vec{\theta}^* \in \Theta \colon f(\vec{\theta}^*) \leq f(\vec{\theta}) \,\,\,\,\,\,\forall \vec{\theta} \in \Theta\}\,,</math>
where <math>\vec{\theta}</math> is an <math>n</math>-dimensional vector that belongs to the set of feasible solutions <math>\Theta</math> (also called solution space). The elements of the set <math>\Theta^*</math> are equivalent with respect to the function <math>f</math>.
Let <math>\mathcal{P} = \{p_{1},p_{2},\ldots,p_{k}\}</math> be the population of particles (also referred to as swarm). At any time step <math>t</math>, a particle <math>p_i</math> has a position <math>\vec{x}^{\,t}_i</math> and a velocity <math>\vec{v}^{\,t}_i</math> associated to it. The best position that particle <math>p_i</math> has ever visited until time step <math>t</math> is represented by vector <math>\vec{b}^{\,t}_i</math> (also known as a particle's personal best). Moreover, a particle <math>p_i</math> receives information from its neighborhood, which is defined as the set <math>\mathcal{N}_i \subseteq \mathcal{P}</math>. Note that a particle can belong to its own neighborhood. In the standard particle swarm optimization algorithm, the particles' neighborhood relations are commonly represented as a graph <math>G=\{V,E\}</math>, where each vertex in <math>V</math> corresponds to a particle in the swarm and each edge in <math>E</math> establishes a neighbor relation between a pair of particles. The resulting graph is commonly referred to as the swarm's population topology.
The algorithm
The algorithm starts with the random initialization of the particles' positions and velocities within an initialization space <math>\Theta^\prime \subseteq \Theta</math>. During the main loop of the algorithm, the particles' velocities and positions are iteratively updated until a stopping criterion is met.
The updating rules are:
<math>\vec{v}^{\,t+1}_i = w\vec{v}^{\,t}_i + \varphi_2\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i) \,,</math>
<math>\vec{x}^{\,t+1}_i = \vec{x}^{\,t}_i +\vec{v}^{\,t+1}_i \,,</math>
where <math>w</math> is a parameter called inertia weight, <math>\varphi_1</math> and <math>\varphi_2</math> are two parameters called acceleration coefficients, <math>\vec{U}^{\,t}_1</math> and <math>\vec{U}^{\,t}_2</math> are two <math>n \times n</math> diagonal matrices with in-diagonal elements distributed in the interval <math>[0,1)\,</math> uniformly at random. Every iteration, these matrices are regenerated, that is, <math>\vec{U}^{\,t+1}_{1,2} \neq \vec{U}^{\,t}_{1,2}</math>. Vector <math>\vec{l}^{\,t}_i</math> is the best position ever found by any particle in the neighborhood of particle <math>p_i</math>, that is, <math>f(\vec{l}^{\,t}_i) \leq f(\vec{b}^{\,t}_j) \,\,\, \forall p_j \in \mathcal{N}_i</math>.
A pseudocode version of the standard PSO algorithm is shown below:
:Inputs Objective function <math>f:\Theta \to \mathbb{R}</math>, the initialization domain <math>\Theta^\prime \subseteq \Theta</math>, the set of particles <math>\mathcal{P} \colon |\mathcal{P}| = k</math>,
the parameters <math>w</math>, <math>\varphi_1</math>, and <math>\varphi_2</math>, and the stopping criterion <math>S</math>
:Output Best solution found
// Initialization
Set t := 0
for i := 1 to k do
Initialize <math>\mathcal{N}_i</math> to a subset of <math>\mathcal{P}</math> according to the desired topology
Initialize <math>\vec{x}^{\,t}_i</math> and <math>\vec{v}^{\,t}_i</math> randomly within <math>\Theta^\prime</math>
Set <math>\vec{b}^{\,t}_i = \vec{x}^{\,t}_i</math>
end for
// Main loop
while <math>S</math> is not satisfied do
// Velocity and position update loop
for i := 1 to k do
Set <math>\vec{l}^{\,t}_i</math> := <math>p_i</math>'s best neighbor according to <math>f</math>
Generate random matrices <math>\vec{U}^{\,t}_1</math> and <math>\vec{U}^{\,t}_1</math>
Set <math>\vec{v}^{\,t+1}_i</math> := <math>w\vec{v}^{\,t}_i + \varphi_1\vec{U}^{\,t}_1(\vec{b}^{\,t}_i - \vec{x}^{\,t}_i) + \varphi_2\vec{U}^{\,t}_2(\vec{l}^{\,t}_i - \vec{x}^{\,t}_i)</math>
Set <math>\vec{x}^{\,t+1}_i</math> := <math>\vec{x}^{\,t}_i + \vec{v}^{\,t+1}_i</math>
end for
// Solution update loop
for i := 1 to k do
if <math>f(\vec{x}^{\,t}_i) \leq f(\vec{b}^{\,t}_i)</math>
Set <math>\vec{b}^{\,t}_i</math> := <math>\vec{x}^{\,t}_i</math>
end if
end for
Set t := t + 1
end while
Main PSO variants
The original particle swarm optimization algorithm has undergone a number of changes since it was first proposed. Most of those changes affect the way the particles' velocity is updated. In the following paragraphs, we briefly describe some of the most important developments. For a more complete description of many of the existing particle swarm optimization variants, we refer the reader to~\cite{Engelbrecht05},~\cite{Clerc06} and~\cite{Poli07}.
Fully informed PSO
In the standard particle swarm optimization algorithm, a particle is attracted toward its best neighbor. A variant in which a particle uses the information provided by all its neighbors in order to update its velocity is called the \emph{fully informed particle swarm} (FIPS)~\cite{Mendes04}.
In the fully informed particle swarm optimization algorithm, the velocity-update rule is \begin{equation} \bvec{v}^{\,t+1}_i = w\bvec{v}^{\,t}_i + \frac{\varphi}{|{\cal N}_i|}\sum_{p_j \in {\cal N}_i}{\cal W}(\bvec{b}^{\,t}_j)\bvec{U}^{\,t}_j(\bvec{b}^{\,t}_j-\bvec{x}^{\,t}_i) \,, \end{equation} where $w$ is a parameter called the \emph{inertia weight}, $\varphi$ is a parameter called \emph{acceleration coefficient}, and ${\cal W} \colon \Theta \to [0,1]$ is a function that weights the contribution of a particle's personal best position to the movement of the target particle based on its relative quality.
Bare bones PSO
A particle swarm optimization algorithm in which the velocity- and position-update rules are substituted by a procedure that samples a parametric probability density function is called the \emph{bare-bones particle swarm}~\cite{Kennedy03}.
In the bare bones particle swarm optimization algorithm, a particle's position update rule in the $j$th dimension is \begin{equation} x^{t+1}_{ij} = N\left(\mu^{t} ,\sigma^{\,t}\right)\,, \end{equation} where $N$ is a normal distribution with \begin{eqnarray*} \mu^{t} &=& \frac{b^{t}_{ij} + l^{t}_{ij}}{2} \,, \\ \sigma^{t} & = & |b^{t}_{ij} - l^{t}_{ij}| \,. \end{eqnarray*}
Although a normal distribution was chosen when it was first proposed, any other probability density function can be used with the bare bones model.
% The idea of replacing the particles' movement rules for a sampling method came after realizing that a particle's next position is % a stochastic variable with a specific probability distribution. (see Section~\ref{Section:Research}, for more information).
Discrete PSO
Although particle swarm optimization algorithms are normally designed to search in continuous domains, there are a number of variants that operate in discrete spaces. One such algorithm is the binary particle swarm optimization algorithm~\cite{Kennedy97b}. In this algorithm, a component of a particle's position vector is interpreted as the probability of that component taking a value of 1. A particle's velocity is updated using Equation~\ref{equation:velocityUpdate}; however, the $j$th component of a particle's position is updated using the following rule \begin{equation} x^{t+1}_{ij} = \begin{cases} 1 & \text{if $r < sig(v^{t+1}_{ij})$,}\\ 0 & \text{otherwise,} \end{cases} \end{equation} where $r$ is a uniformly distributed random number in the range $[0,1)$ and \begin{equation} sig(x) = \frac{1}{1+e^{-x}}\,. \end{equation}
Other approaches to tackle discrete problems include rounding off the components of the particles' position vectors~\cite{Laskari02}, transforming the continuous domain into discrete sets of intervals~\cite{Fukuyama99}, redefining the mathematical operators used in the velocity- and position-update rules to suit a chosen problem representation~\cite{Clerc04}, and the stochastic instantiation of solution values to the discrete problem based on probabilities defined by the traditional rules~\cite{Pugh06}.
Multiobjective PSO
The particle swarm optimization algorithm has also been adapted to tackle {\bf multiobjective optimization problems}~\cite{Reyes06}. The main differences between traditional single-objective particle swarm optimization algorithms and their multiobjective counterparts are:
- Leader selection. In multiobjective optimization problems there is no single best solution that dominates all the others. The challenge, therefore, is to select from among equally good solutions one that can guide a particle toward the true Pareto front of the problem.
- Output set generation. The output of a multiobjective optimizer is the set of nondominated solutions found during the whole run of the algorithm. The common approach used in multiobjective particle swarm optimization algorithms is to maintain a solution archive in which the set of nondominated solutions are stored.
- Diversity mechanisms. To find diverse solutions that spread across the problem's Pareto front, multiobjective optimization algorithms must maintain a high level of diversity so as to avoid convergence to a single solution. In multiobjective particle swarm optimizers an extra mutation operator is usually added for this purpose.
Applications of PSO
Particle swarm optimization algorithms have been applied in many domains, including neural networks (the first application of these algorithms), telecommunications, data mining, combinatorial optimization, power systems, signal processing, and many others. There are hundreds of publications reporting applications of particle swarm optimization algorithms. For a review, please see~\cite{Poli08a}.
Current Research Issues
Current research in particle swarm optimization is done along several lines. Some of them are:
\begin{description} \item[Theory.] Understanding how particle swarm optimizers work, from a theoretical point of view, has been the subject of active research in the last years. The first efforts were directed toward understanding the effects of the different parameters in the behavior of the standard particle swarm optimization algorithm~\cite{Ozcan99,Clerc02,Trelea03}. In recent years there has been a particular interest in studying the stochastic properties of the pair of stochastic equations that govern the movement of a particle~\cite{Blackwell07,Poli08b,Pena08}.
\item[New variants.] This line of research has been the most active since the proposal of the first particle swarm algorithm.
New particle position-update mechanisms are continuously proposed in an effort to design ever better performing particle swarms.
Some efforts are directed toward understanding on which classes of problems particular particle swarm algorithms can be top
performers~\cite{Poli05a,Poli05b,Langdon07}. Also of interest is the study of hybridizations between particle swarms and other
high-performing optimization algorithms~\cite{Lovbjerg01,Naka03}. Recently, some parallel implementations have been studied~\cite{Schutte04,Koh06}
and due to the wider availability of parallel computers, we should expect more research to be done along this line.
\item[Performance evaluation.] Due to the great number of new variants that are frequently proposed, performance comparisons have been always of interest. Comparisons between the standard particle swarm and other optimization techniques, like the ones in ~\cite{Eberhart98,Hassan05}, have triggered the interest of many researchers on particle swarm optimization. Comparisons between different particle swarm optimization variants or empirical parameter settings studies help in improving our understanding of the technique and many times trigger empirical and theoretical work~\cite{Mendes04,Schutte05,MdeO06}.
\item[Applications.] It is expected that in the future more applications of the particle swarm optimization algorithm will be considered. Much of the work done on other aspects of the paradigm will hopefully allow us to solve practically relevant problems in many domains.
\end{description}
Notes
<references />
References
F. Heppner and U. Grenander. A stochastic nonlinear model for coordinated bird fl ocks. The Ubiquity of Chaos. AAAS Publications, Washington, DC. 1990.
J. Kennedy and R. Eberhart. Particle swarm optimization. In Proceedings of IEEE International Conference on Neural Networks, pages 1942-1948, IEEE Press. Piscataway, NJ. 1995.
M. M. Millonas. Swarms, phase transitions, and collective intelligence. Artificial Life III, pages 417-445. Addison-Wesley, Reading, MA. 1994.
W. T. Reeves. Particle systems-a technique for modeling a class of fuzzy objects. ACM Transactions on Graphics, 2(2):91-108, 1983.
C. W. Reynolds. Flocks, herds, and schools: A distributed behavioral model. ACM Computer Graphics,21(4):25-34, 1987.
External Links
- Many journals and conferences publish papers on PSO:
- The main journal reporting research on PSO is Swarm Intelligence. Other journals where papers on PSO regularly appear are IEEE Transactions on Evolutionary Computation, etc.
- GECCO, ANTS, IEEE SIS, Evo\*
See also
Optimization, Stochastic Optimization, Swarm Intelligence, Ant Colony Optimization