|
 |
by Leslie Pérez Cáceres, Manuel López Ibáñez,
Thomas Stützle
2015
| Table of Contents |
Ant Colony Optimization (ACO) is a successful method for solving
difficult combinatorial optimization problems. Following Ant System,
the first ACO algorithm, a large number of algorithmic variants have
been developed that showed significantly better performance on a
wide range of optimization problems. Typically, performance was
measured according to the solution quality achieved for a given
computation time limit, which usually allowed the evaluation of a
very large number of candidate solutions, often in the range of
millions. However, there are practical applications where the number
of evaluations that can be done is very restricted be it due to
tight real-time constraints or due to the high computational cost of
evaluating a solution in areas such as simulation based
optimization. Since these situations are quite different from those
for which ACO algorithms were initially designed, the current
knowledge on good parameter settings or the most promising search
strategies may not be directly applicable. In this paper, we examine
the performance of different ACO algorithms under a strongly limited
budget of, say, 1\,000 evaluations. We do so using default parameter
settings from the literature and parameter settings tuned for the
limited budget scenario. In addition, we compare the performance of
the ACO algorithms to algorithms that make use of surrogate modeling
of the search landscapes. We show that tuning algorithms for the
limited budget case is of uttermost importance, direct search
through the ACO algorithms keeps an edge over techniques using
surrogate modeling and the ACO variants proposed as improvements
over Ant System remain preferable.
Keywords: ant colony optimization, ACOTSP, parameter
setting, Efficient global optimisation
In this work we used five ACO algorithms:
The use implementation of these algorithms corresponds to ACOTSP software, a freely available framework that contains implementation of well known ACO algorithms. For the TSP the algorithm used in these experiments is based on the version 1.02 of ACOTSP, we eliminate the use of the nearest neighbour list in the construction phase. For QAP we use an adaptation of ACOTSP for solving QAP.
| algorithm | ants | alpha | rho | q0 | beta | rasrank | elitistants |
|---|---|---|---|---|---|---|---|
| AS | 75/80 (n) | 0.5 | 0.00 | 1 | 2/0 | − | − |
| EAS | 75/80 (n) | 0.5 | 0.00 | 1 | 2/0 | − | #ants |
| RAS | 75/80 (n) | 0.1 | 0.00 | 1 | 2/0 | 6 | − |
| MMAS | 75/80 (n) | 0.02 | 0.00 | 1 | 2/0 | − | − |
| ACS | 10/10 | 0.1 | 0.90 | 1 | 2/0 | − | − |
The EGO algorithm used for TSP and QAP is implemented in C++ is
available here [TSP | QAP]. This implementation uses the Eigen C++ library , make sure you add the path to it in the makefile.
We base the implementation in the EGO
adaptation to permutation problems in [8]. We limit the number of
solutions used for fitting the Kriging model to 300. When more
solutions are available, we discard the solution with the smallest
average distance to the rest of the solution set. If you use this code
please cite:
Ant colony optimization on a limited budget of evaluations. Leslie Pérez Cáceres, Manuel López-Ibáñez and Thomas Stützle. Swarm Intelligence, Volume 9, Issue 2, Pages 103--124. Springer US, 2015.
We solved two classical NP−hard combinatorial optimization problems.
The relevant parameters for every algorithm/problem are summarized in the table below.
| Common to all | RAS and EAS | TSP | ||||
|---|---|---|---|---|---|---|
| ants | alpha | rho | q0 | rasrank | elitistants | beta |
| [5, 100] | [0, 10] | [0.01, 1] | [0, 1] | [1, 100] | [1, 175] | [0, 10] |
We performed the tuning of the algorithms described for the tackled problems, we used irace as auotmatic configuration tool. Irace is available as an R package.
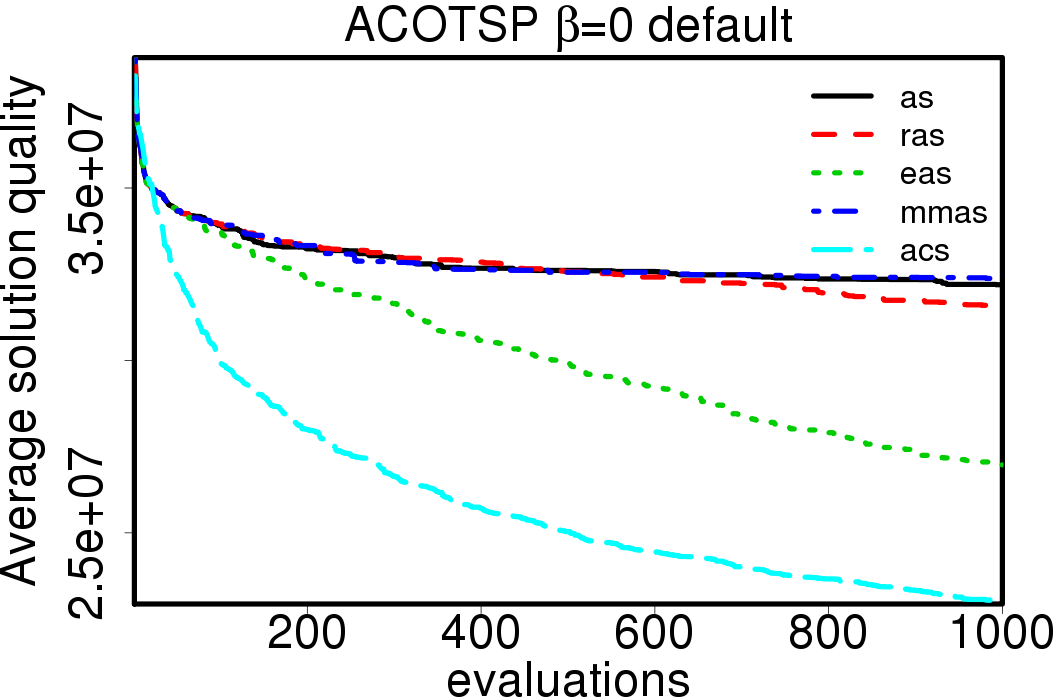
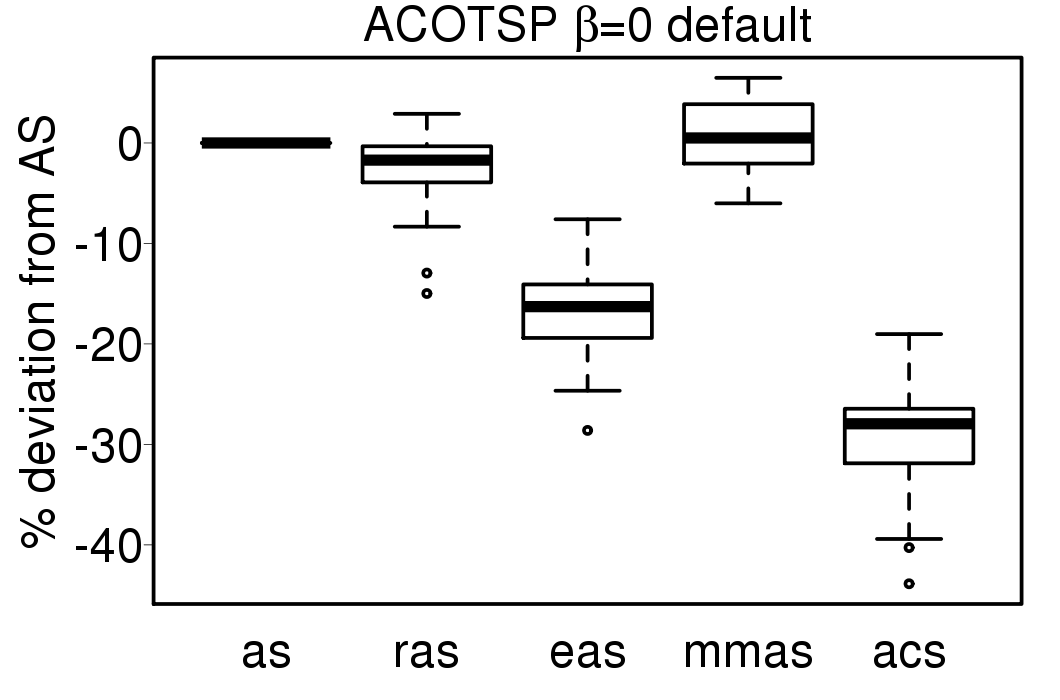
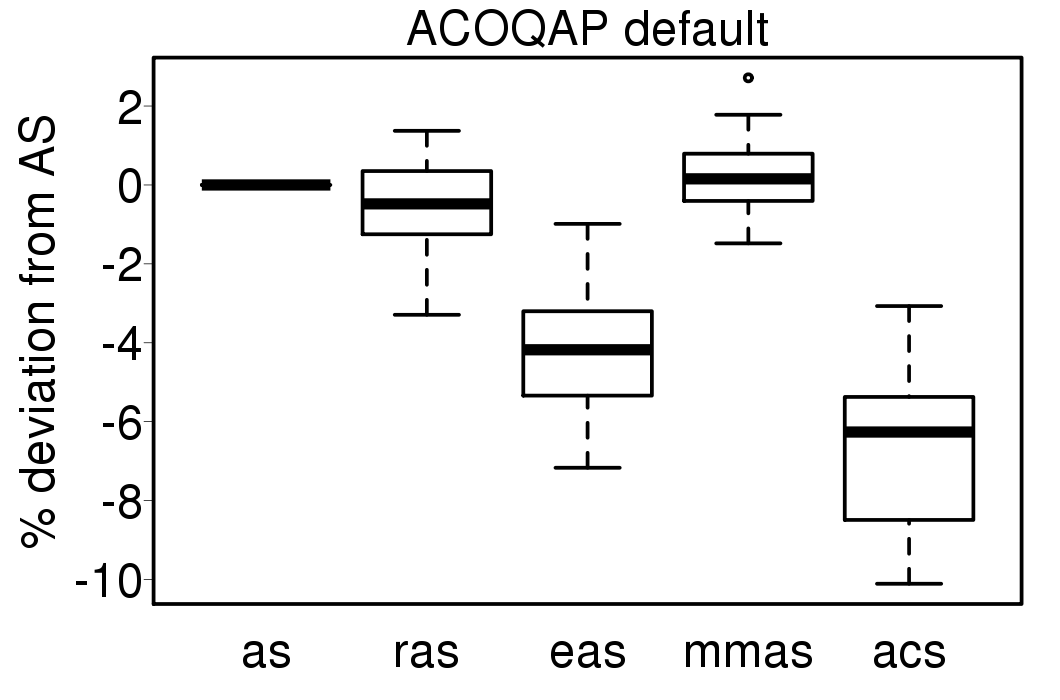
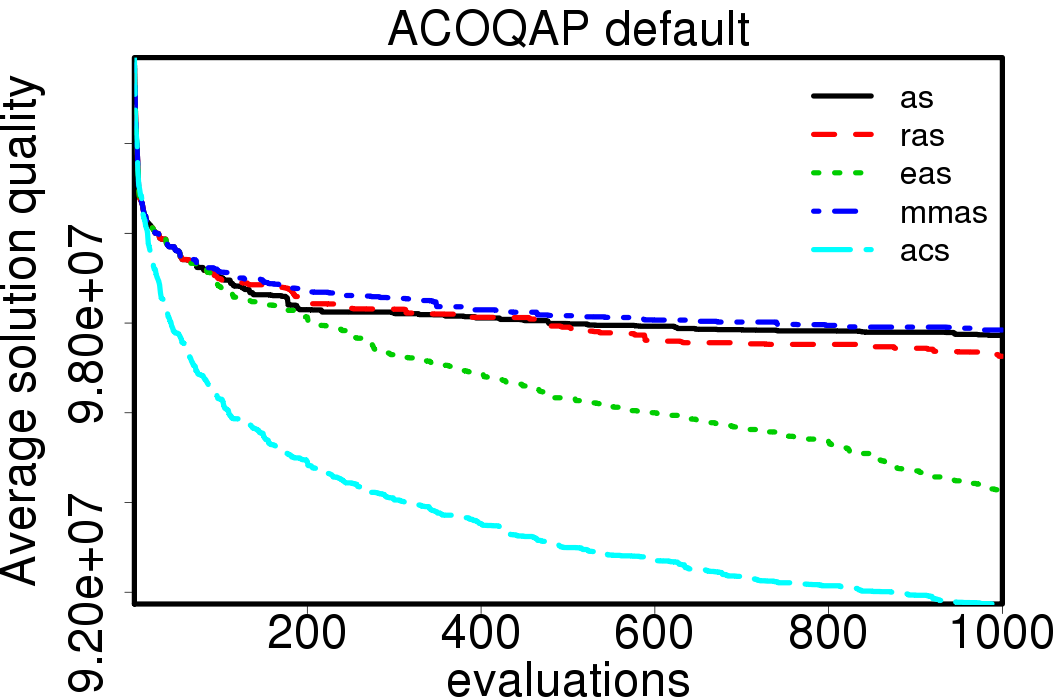
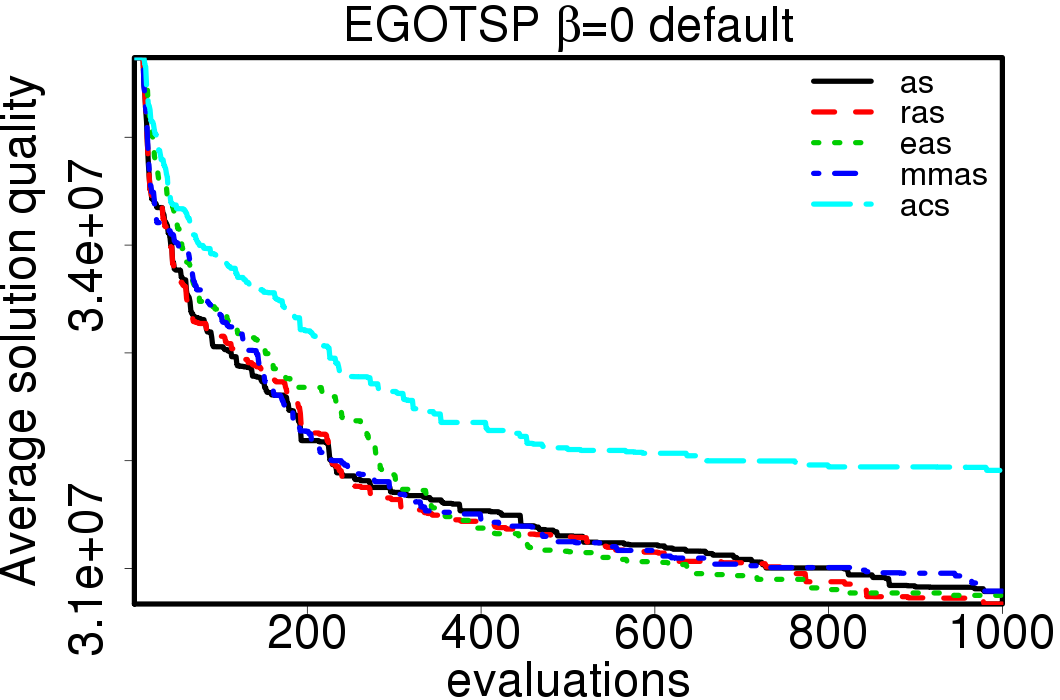
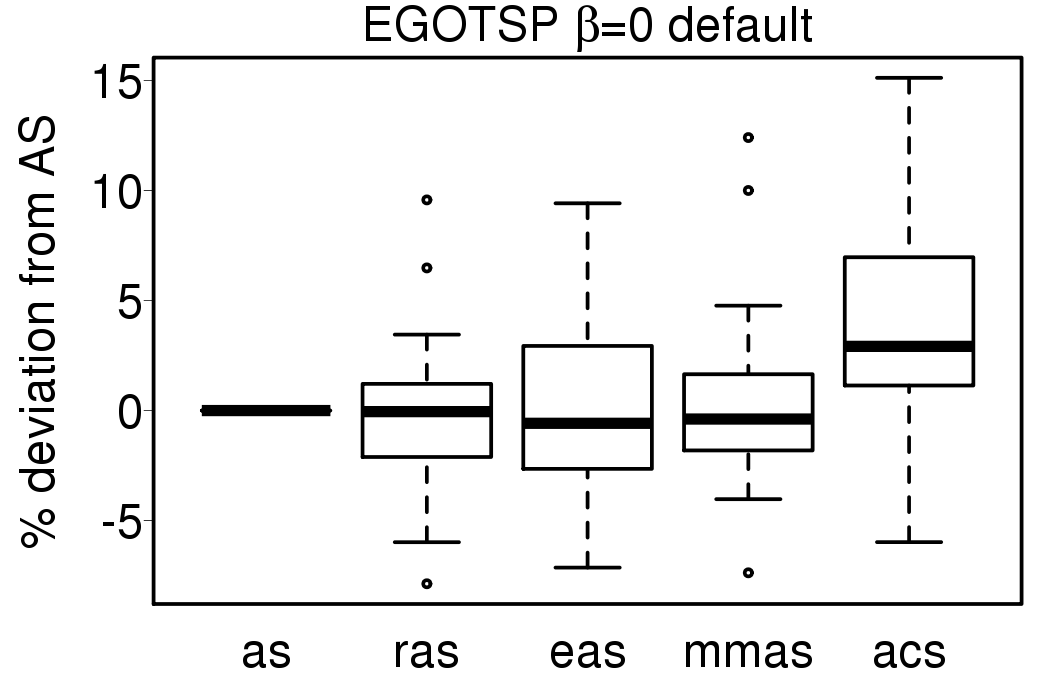
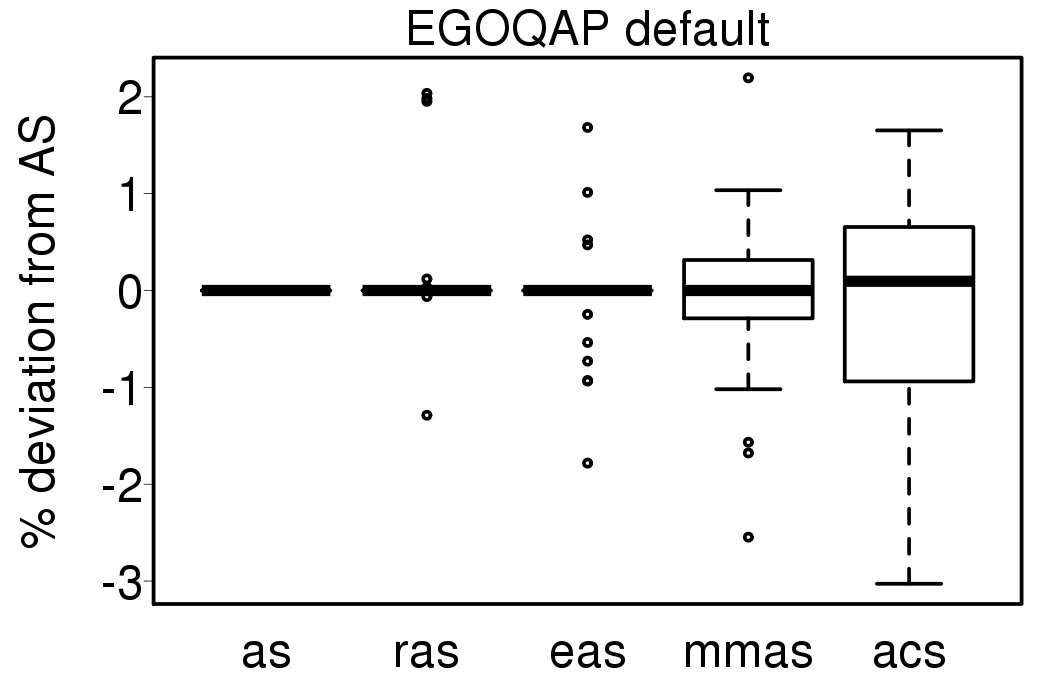
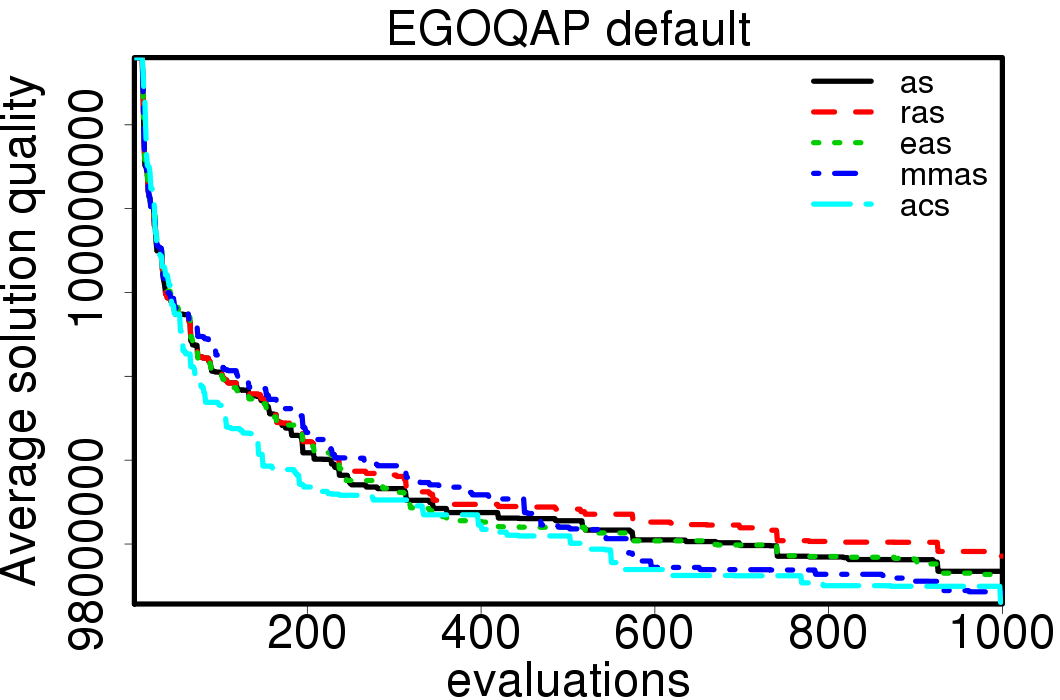
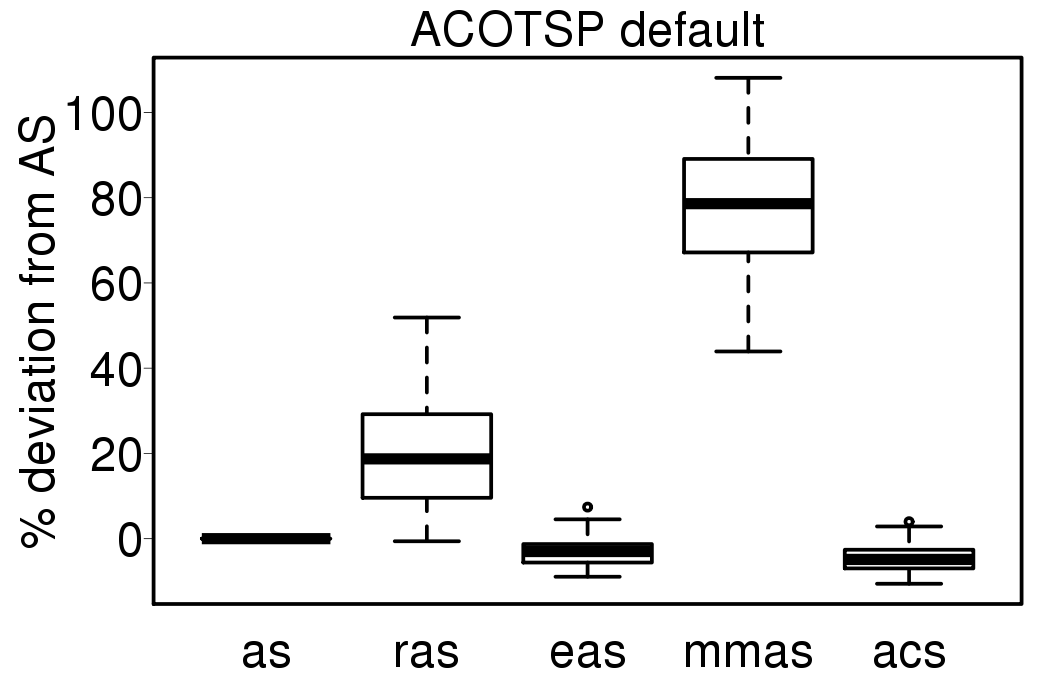
We compared the performance of the ACO algorithms when using its default settings and without heuristic information:


|

 |
We performed the tuning using the tune-ACOTSP and tune-ACOQAP scenarios, Table 3 show the obtained values:
| algorithm | ants | alpha | rho | q0 | rasrank | elitistants |
|---|---|---|---|---|---|---|
| AS | 44 / 71 | 1.08 / 0.53 | 0.44 / 0.32 | 0.07 / 0.53 | − | − |
| EAS | 8 / 9 | 0.76 / 0.51 | 0.32 / 0.34 | 0.05 / 0.68 | − | 221 / 148 |
| RAS | 35 / 32 | 1.31 / 0.78 | 0.72 / 0.74 | 0.16 / 0.36 | 10 / 8 | − |
| MMAS | 9 / 14 | 1.51 / 1.07 | 0.23 / 0.60 | 0 / 0.36 | − | − |
| ACS | 10 / 5 | 6.87 / 2.24 | 0.08 / 0.41 | 0.25 / 0.03 | − | − |
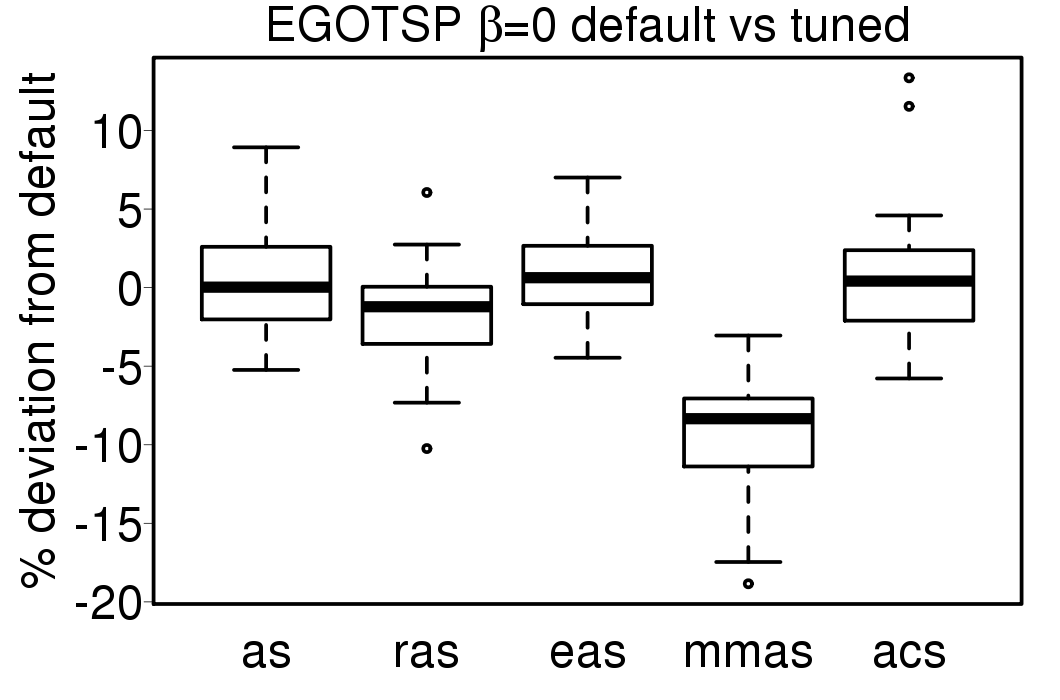
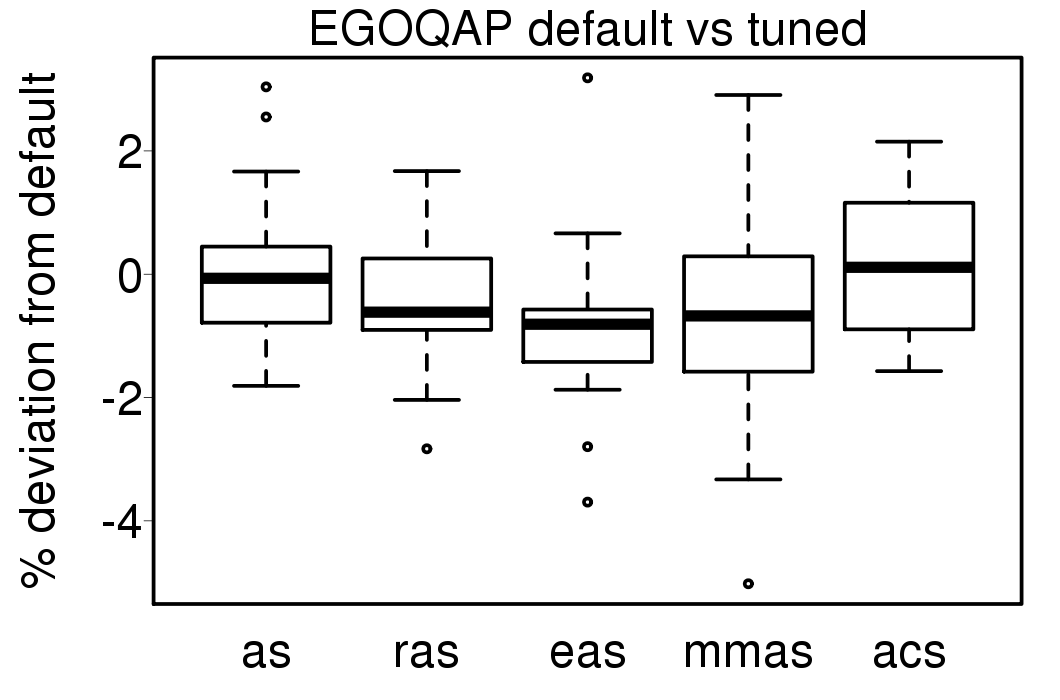
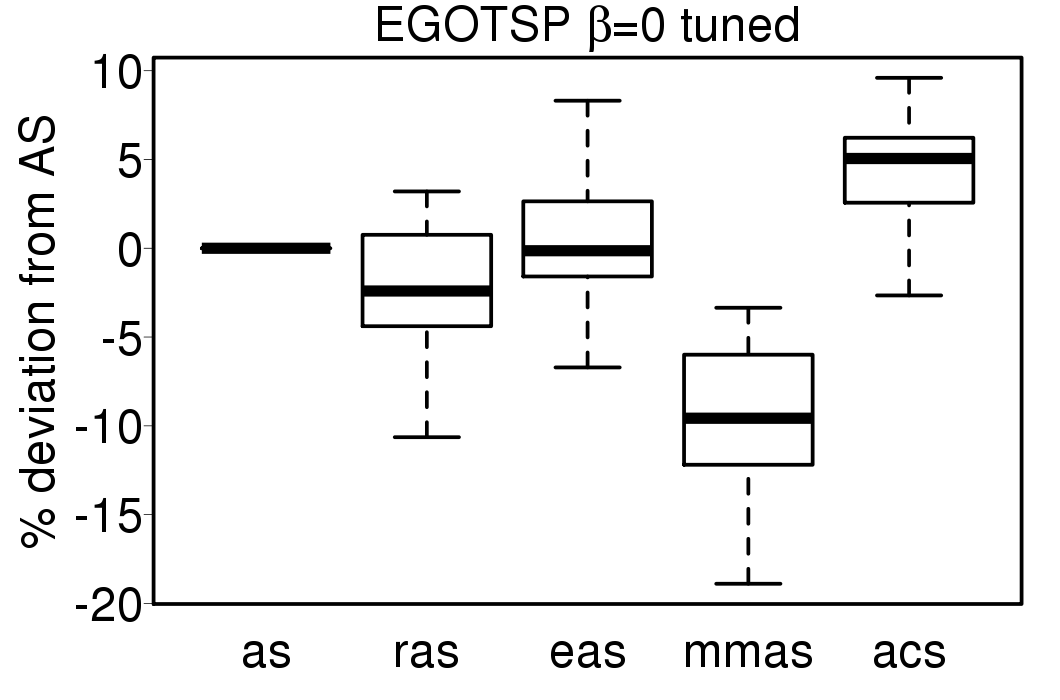
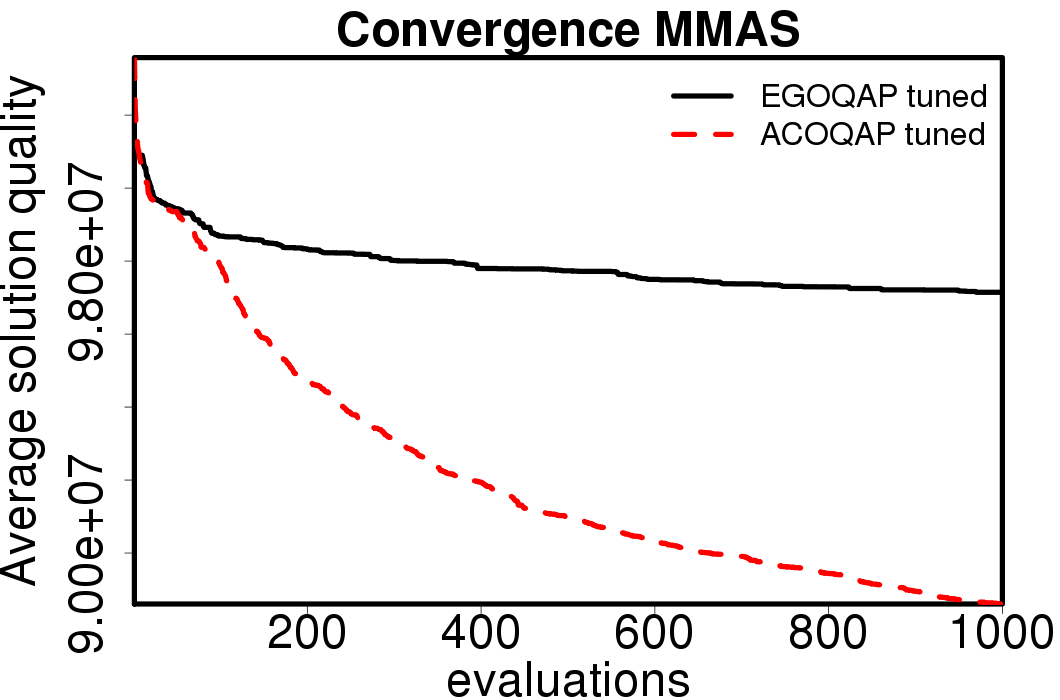
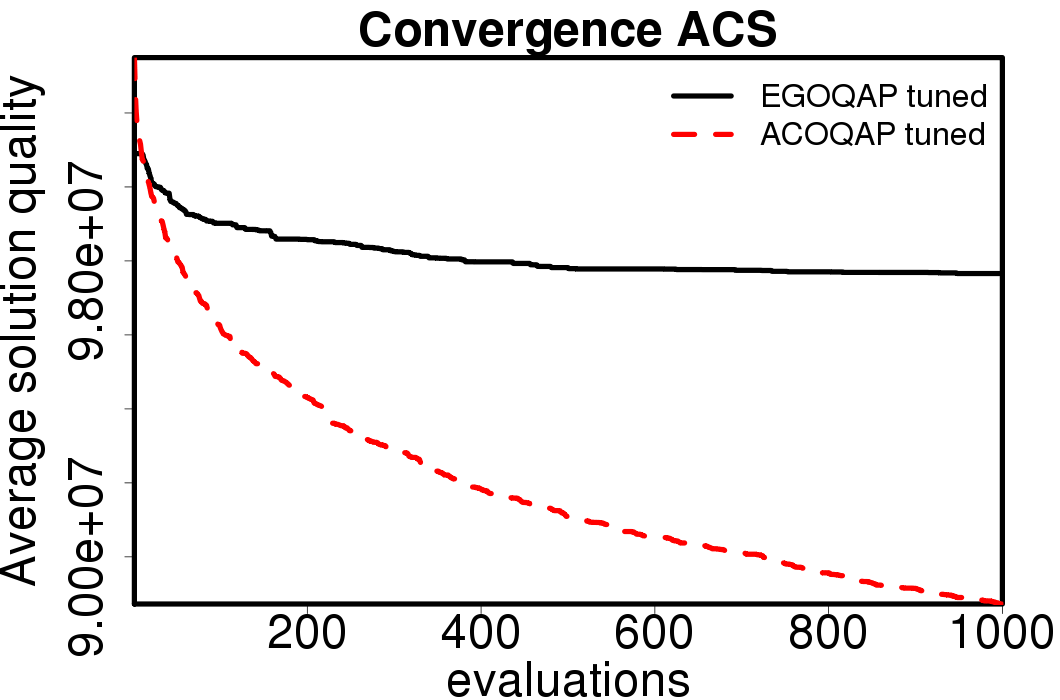
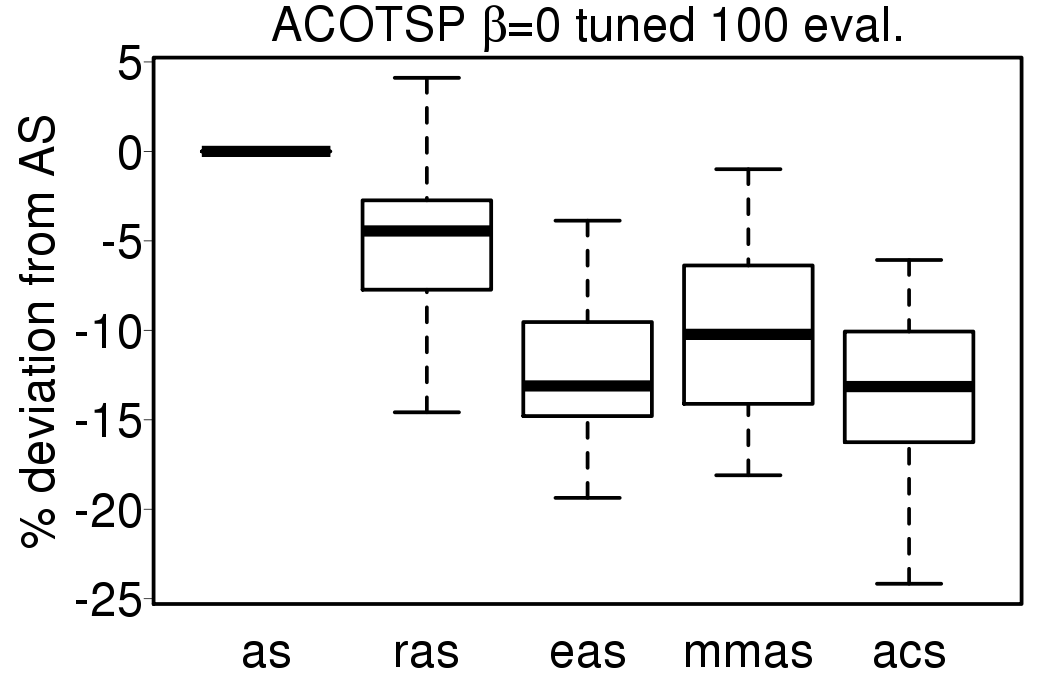
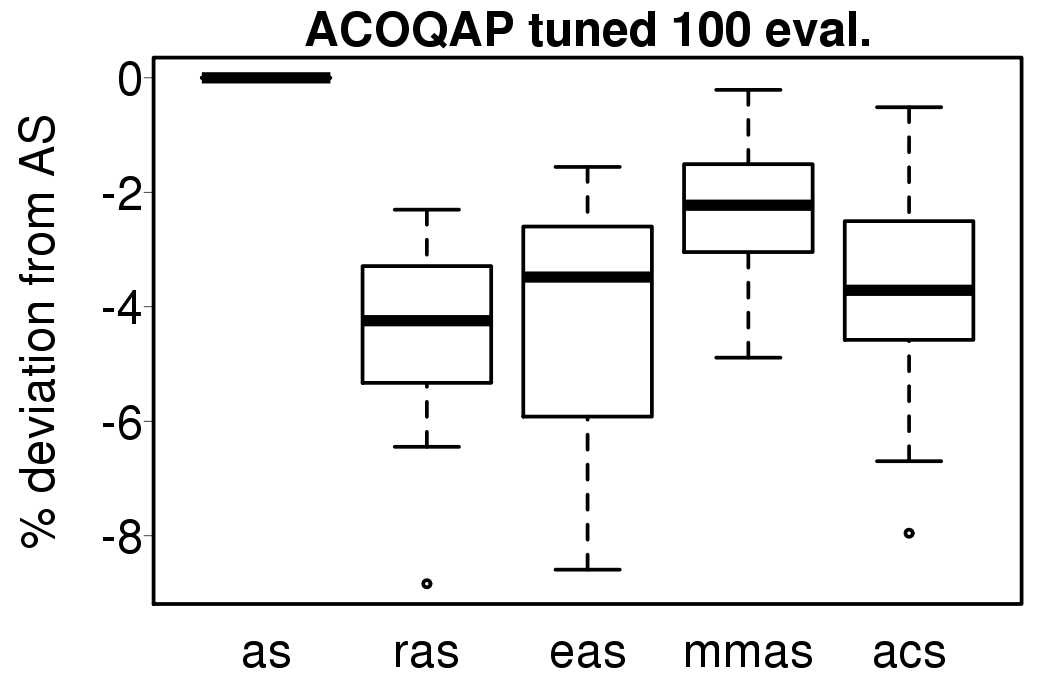
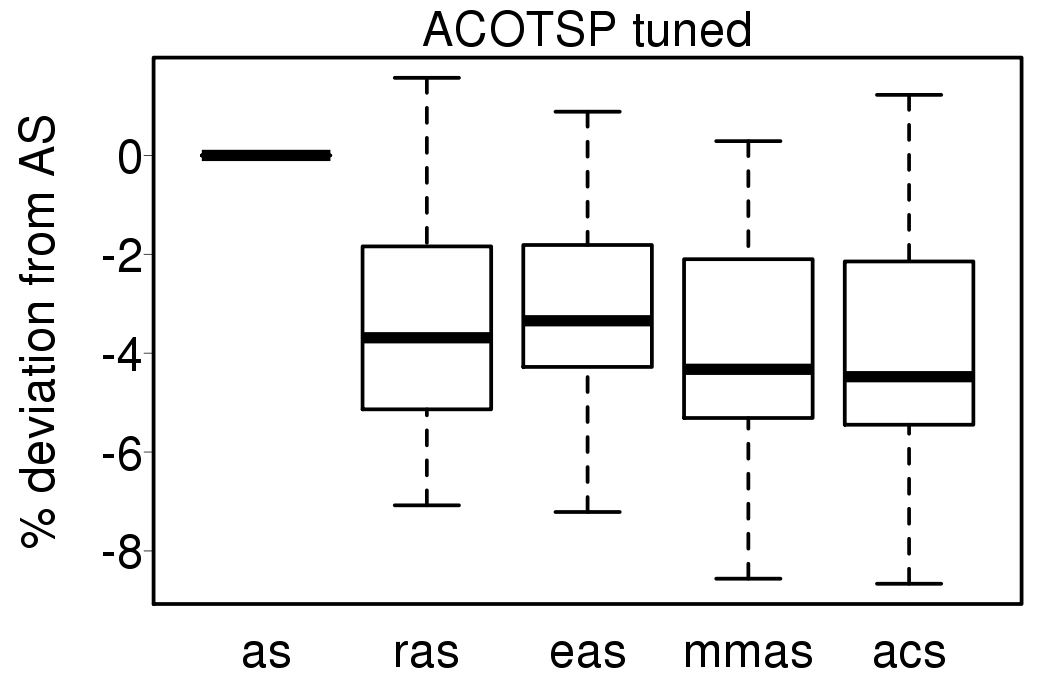
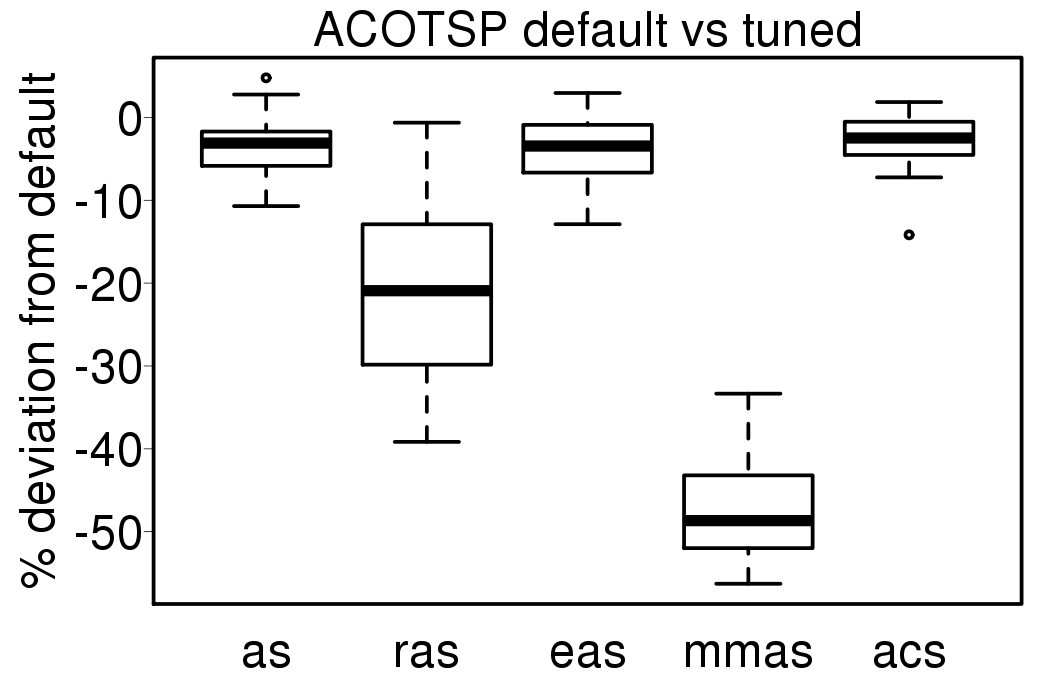
We apply these parameter settings and except AS all the ACO algorithms improve their performance. The relative performance also visible changes. The following plots show the relative performance of the algorithms using AS as base:
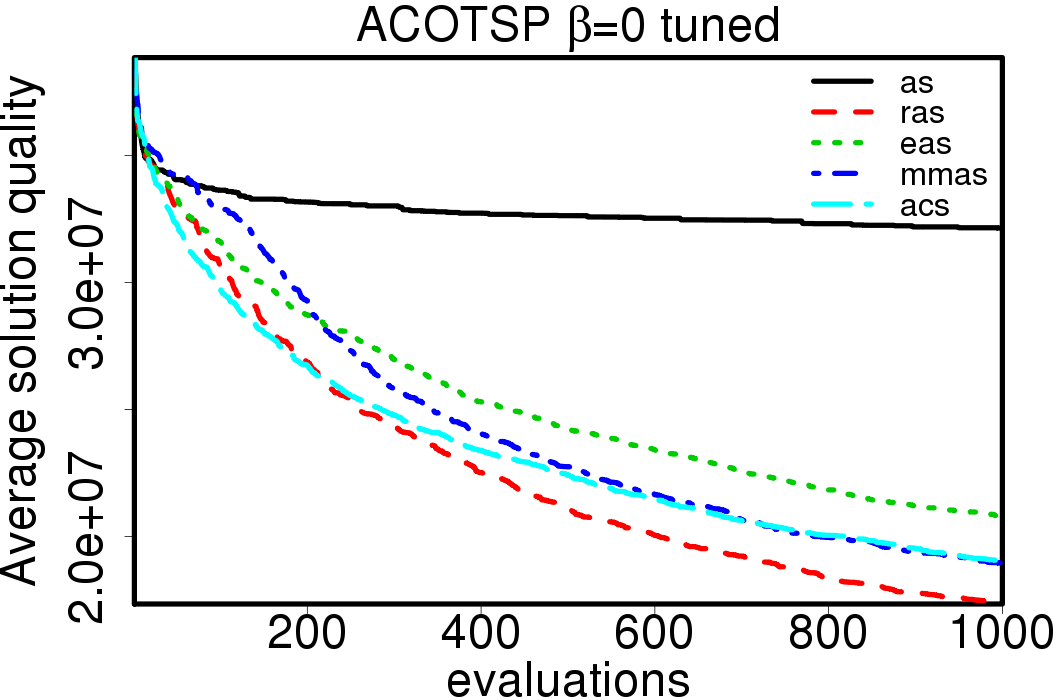
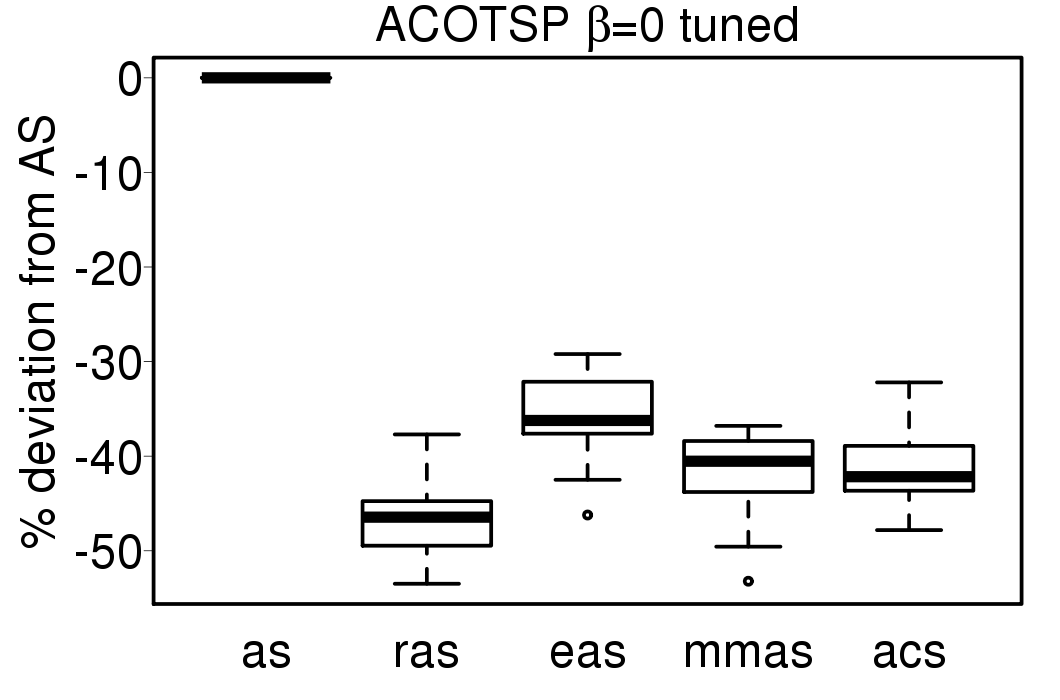 |
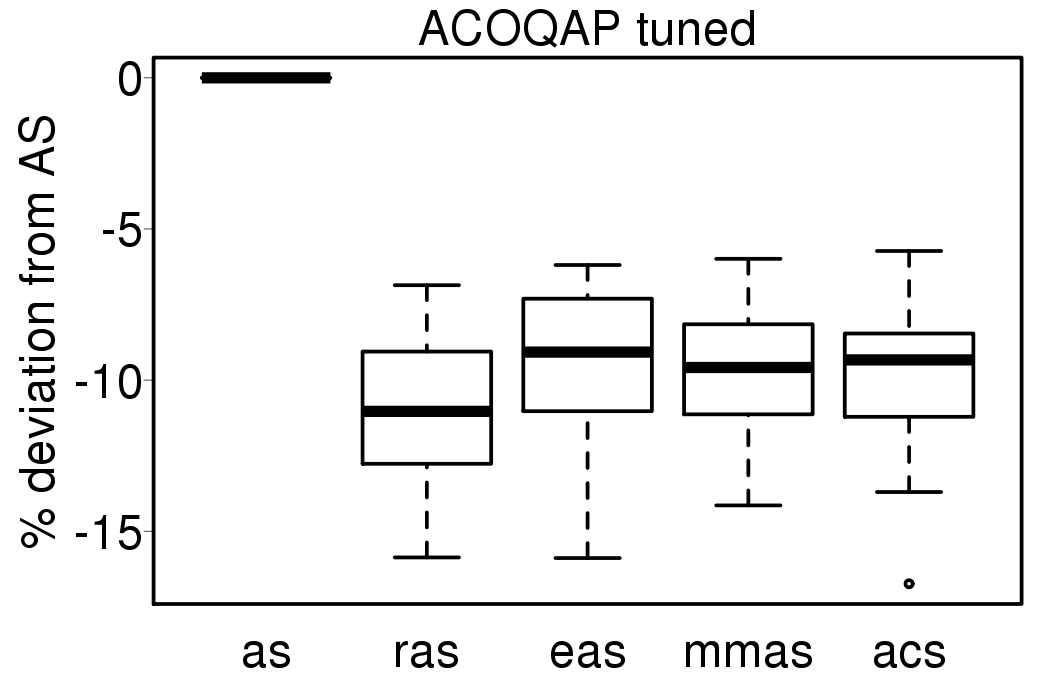 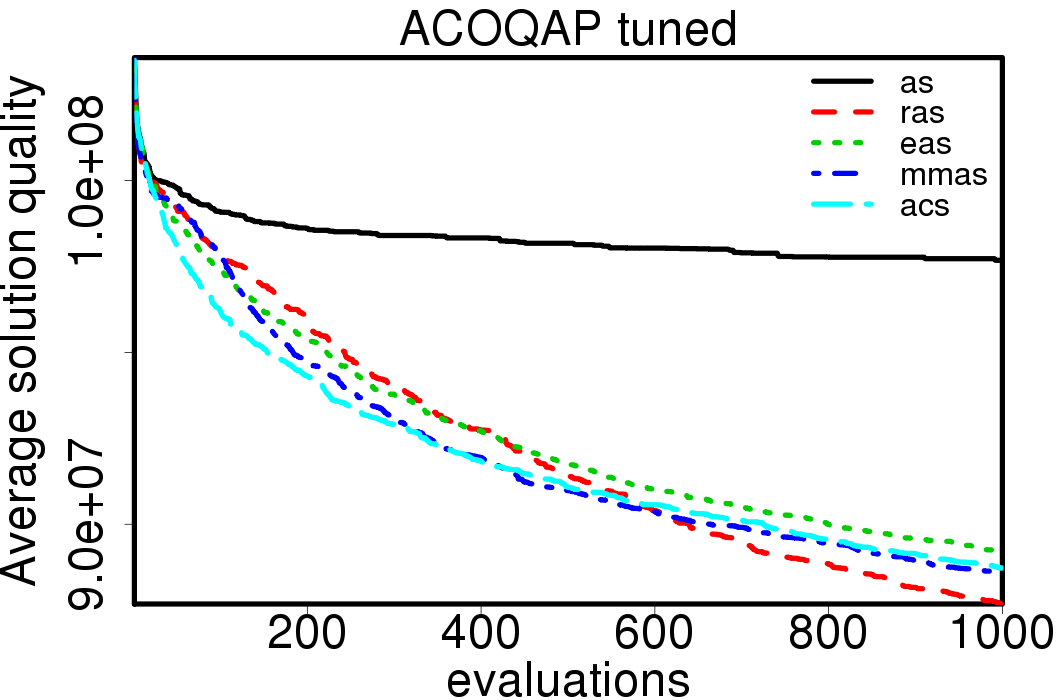 |
The following plot show the solution quality deviation of the ACO algorithms using the tuned settings from the results using default settings:
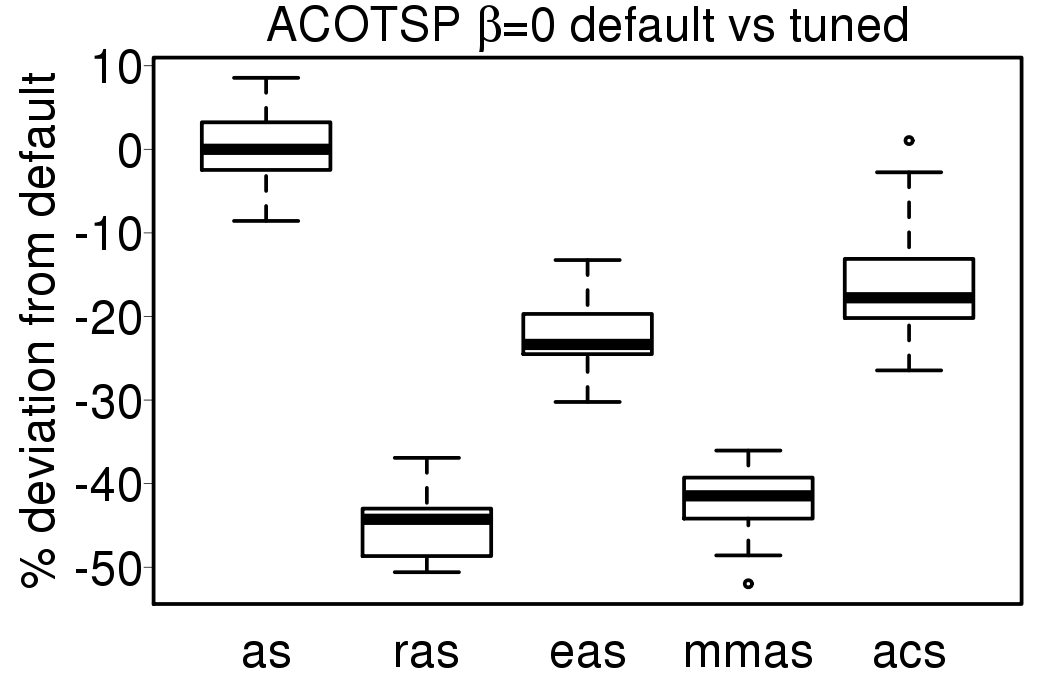 |
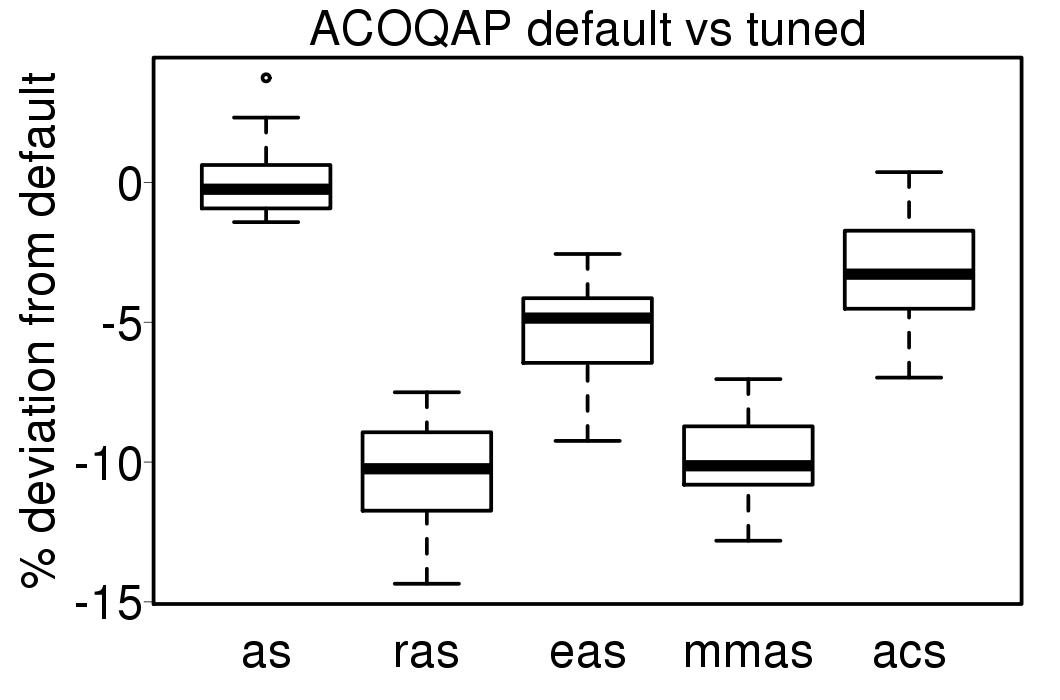 |
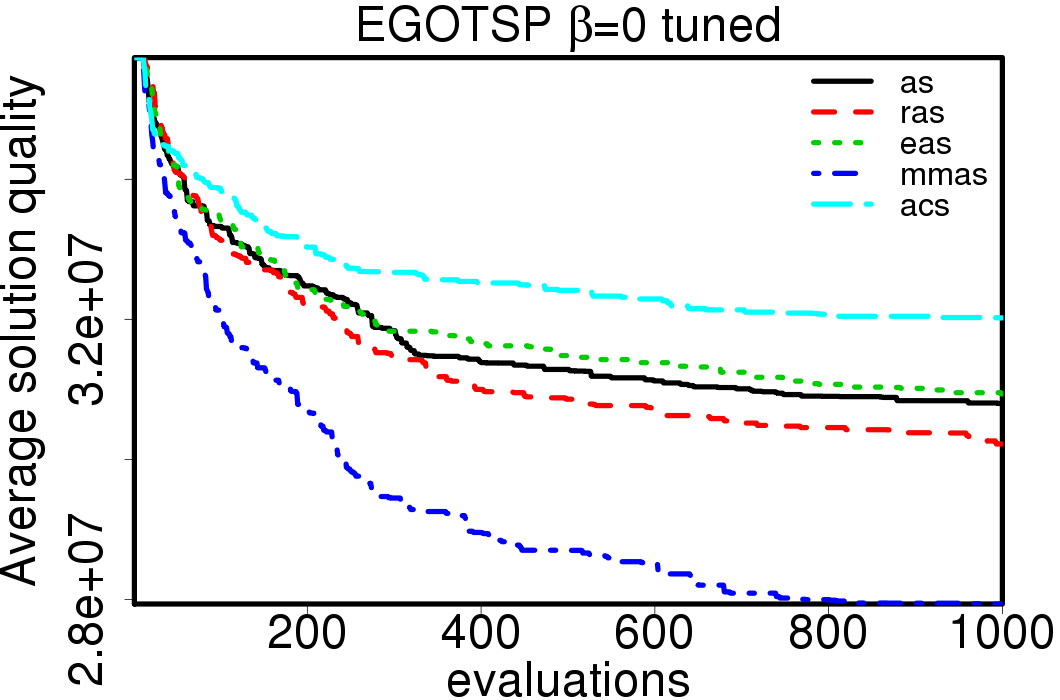
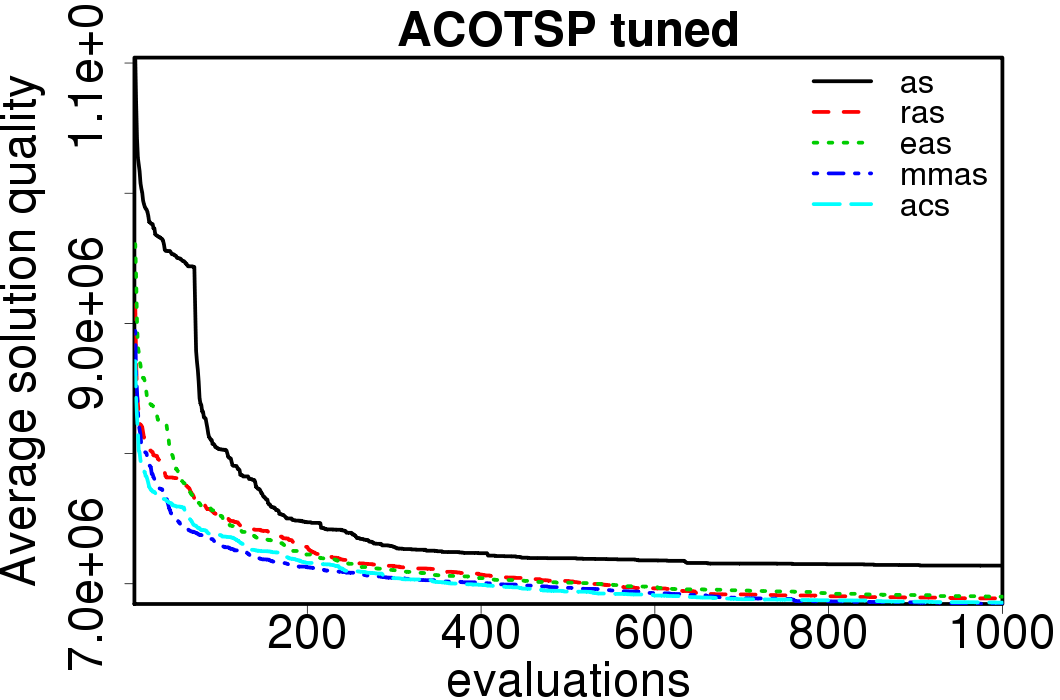
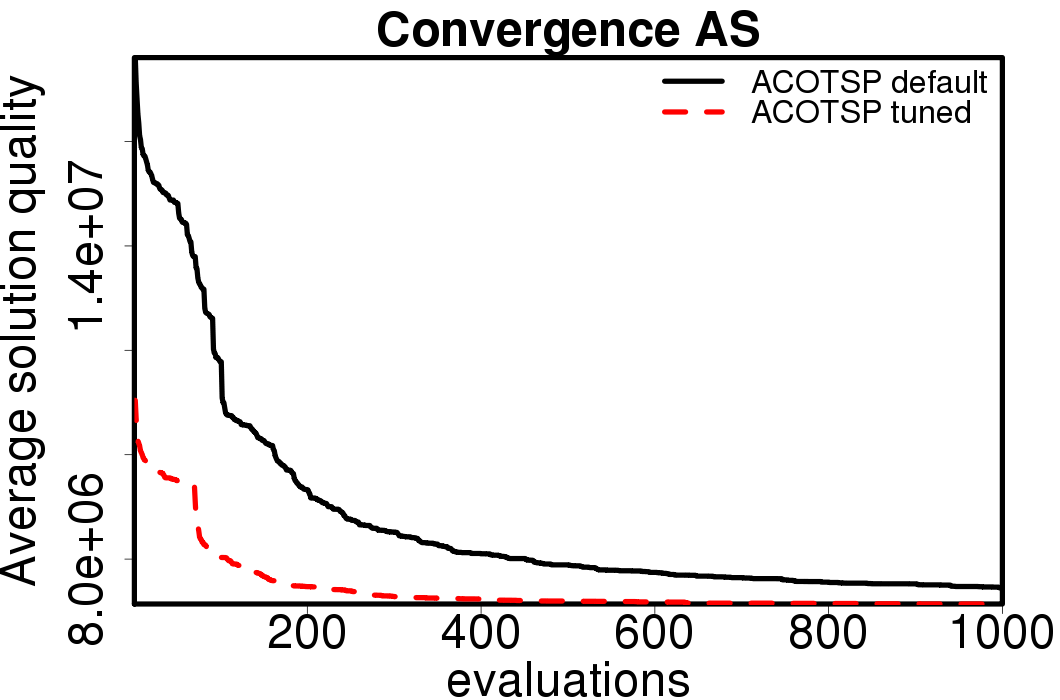
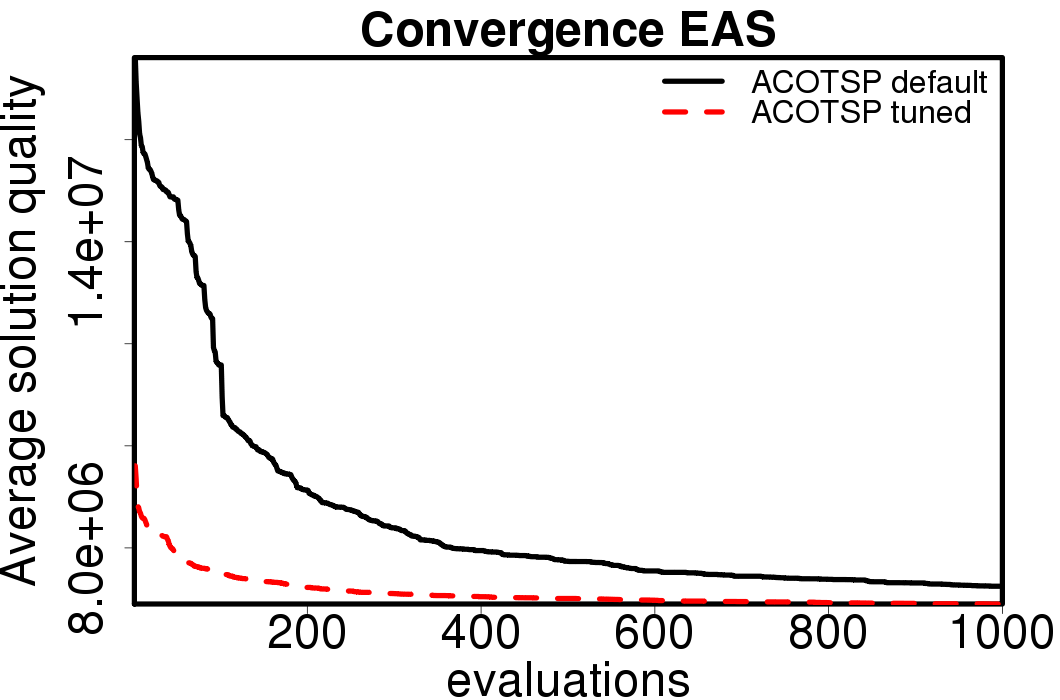
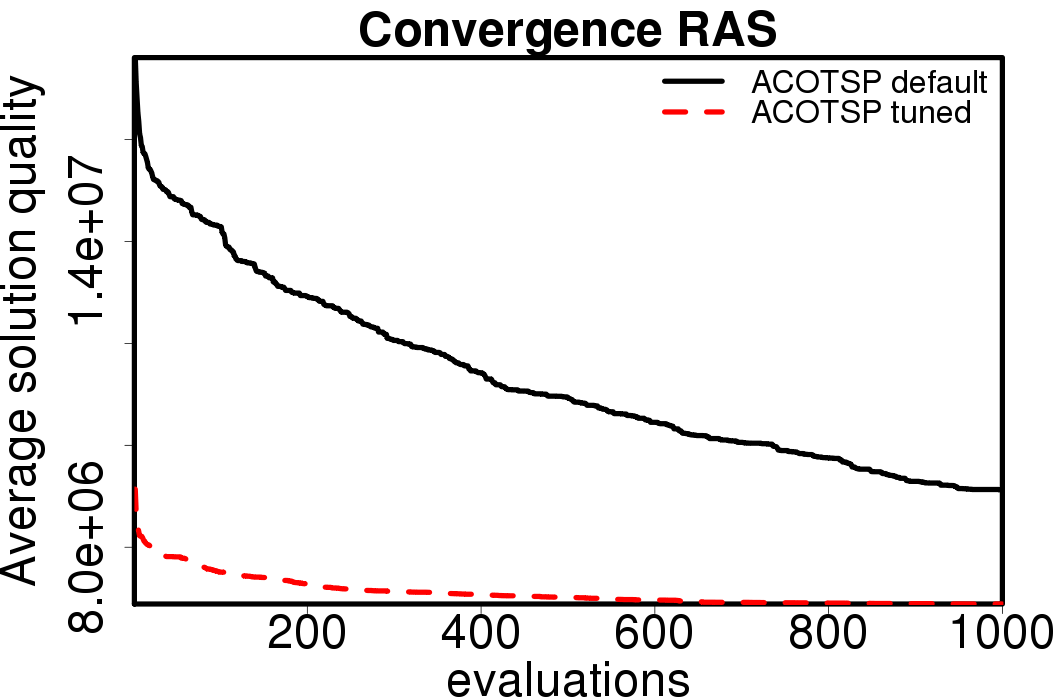
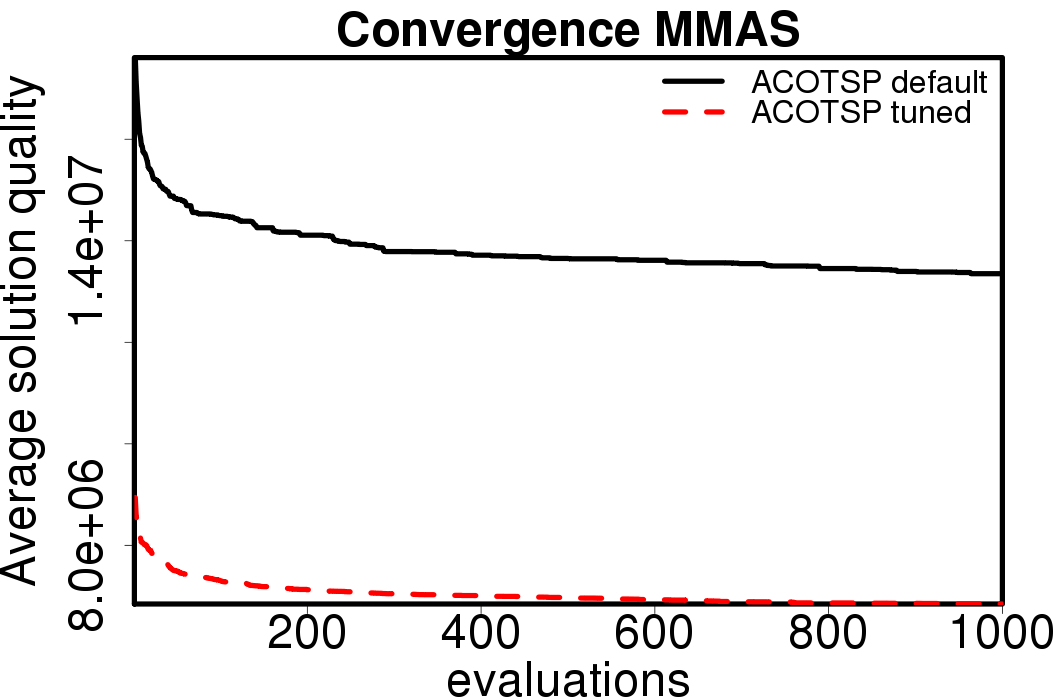
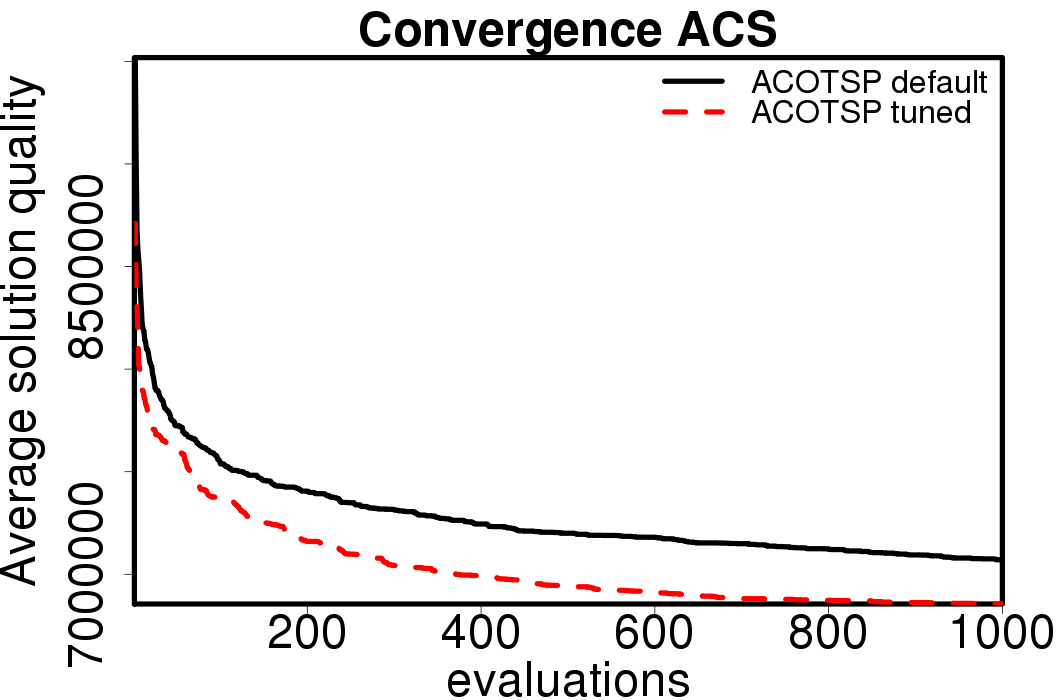
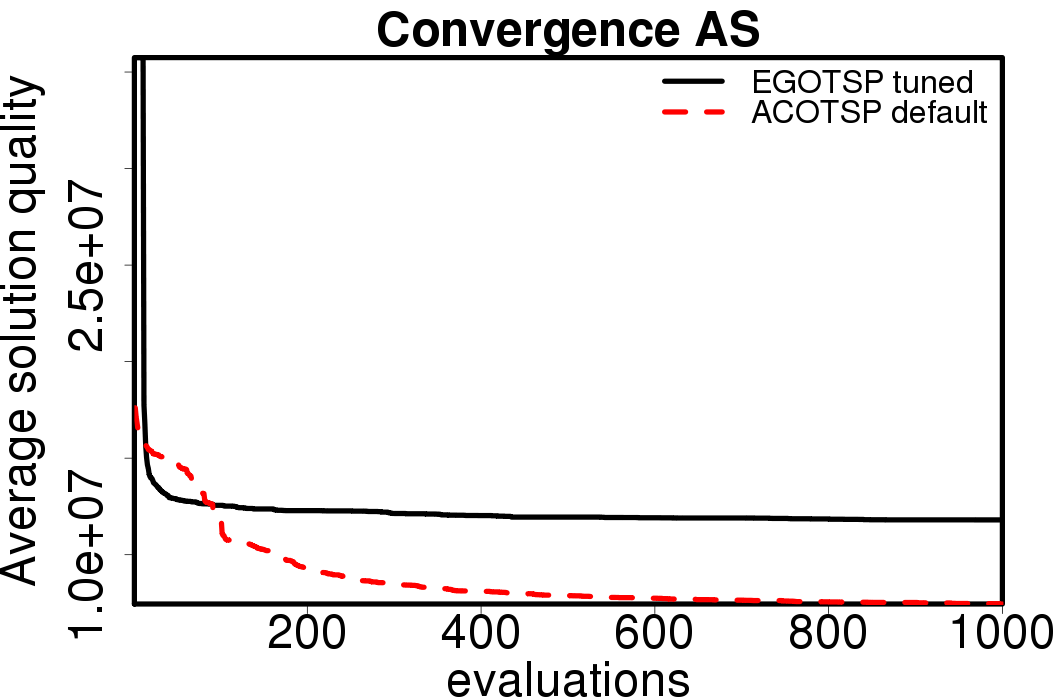
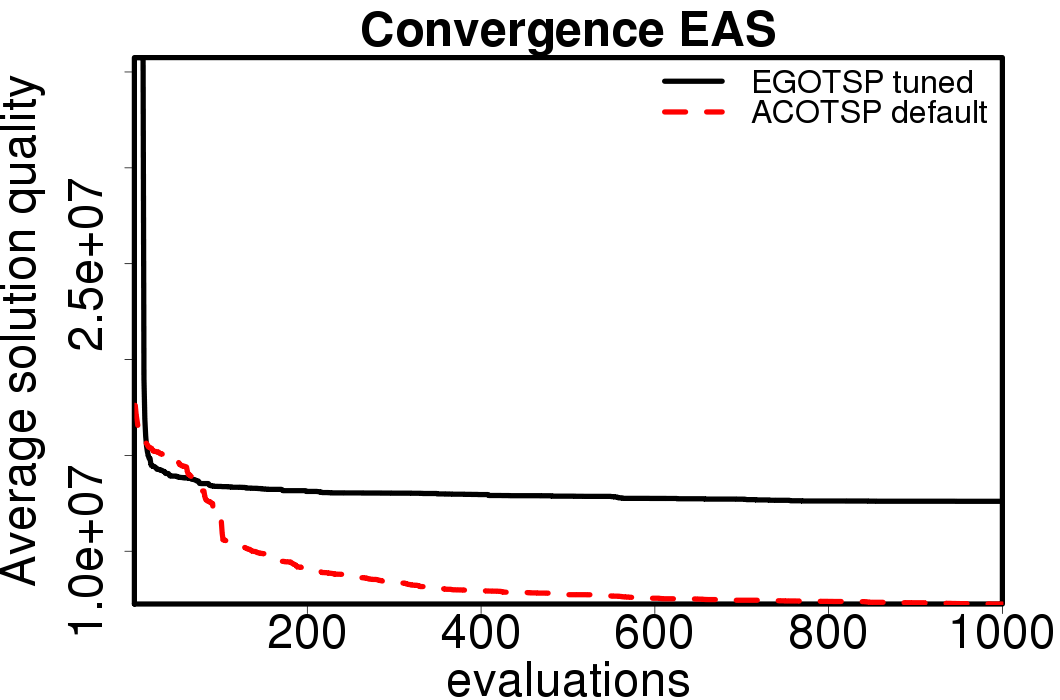
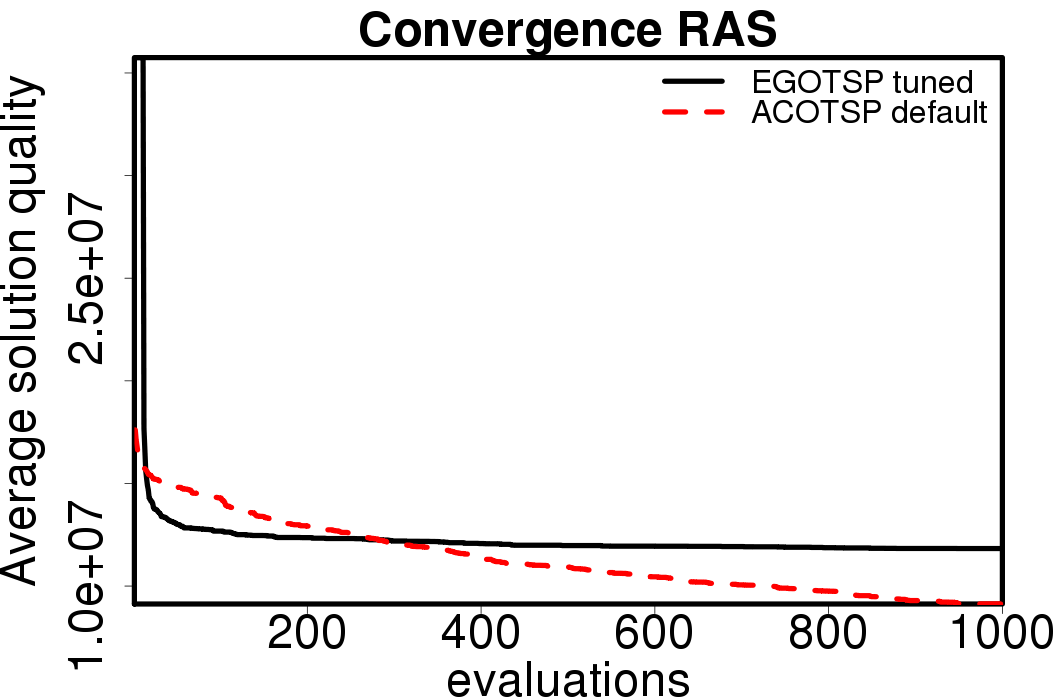
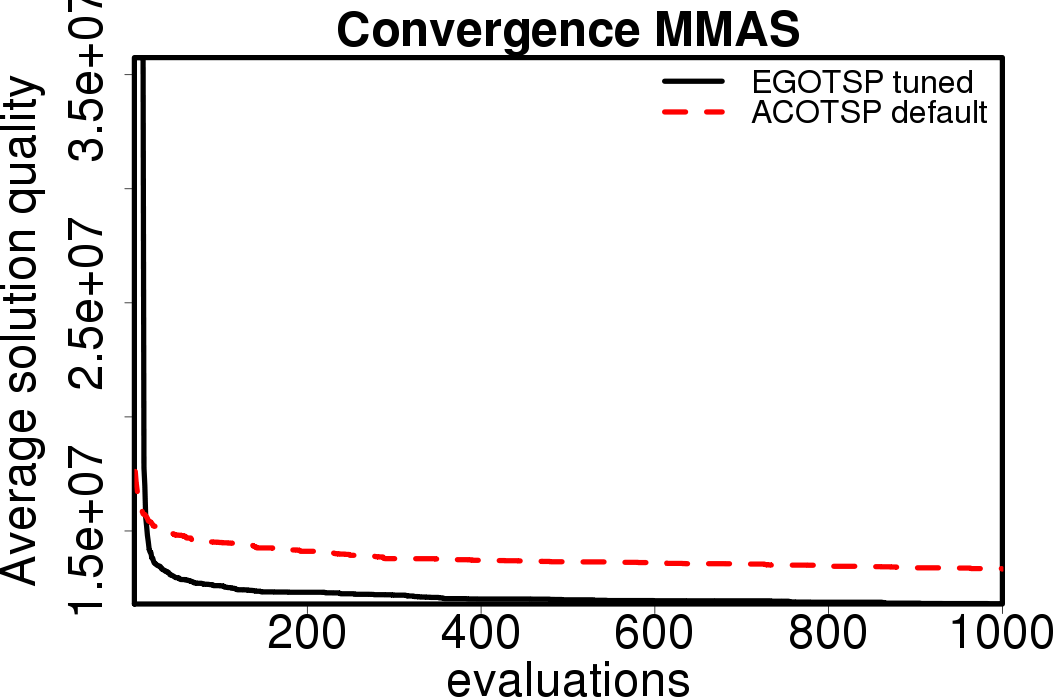
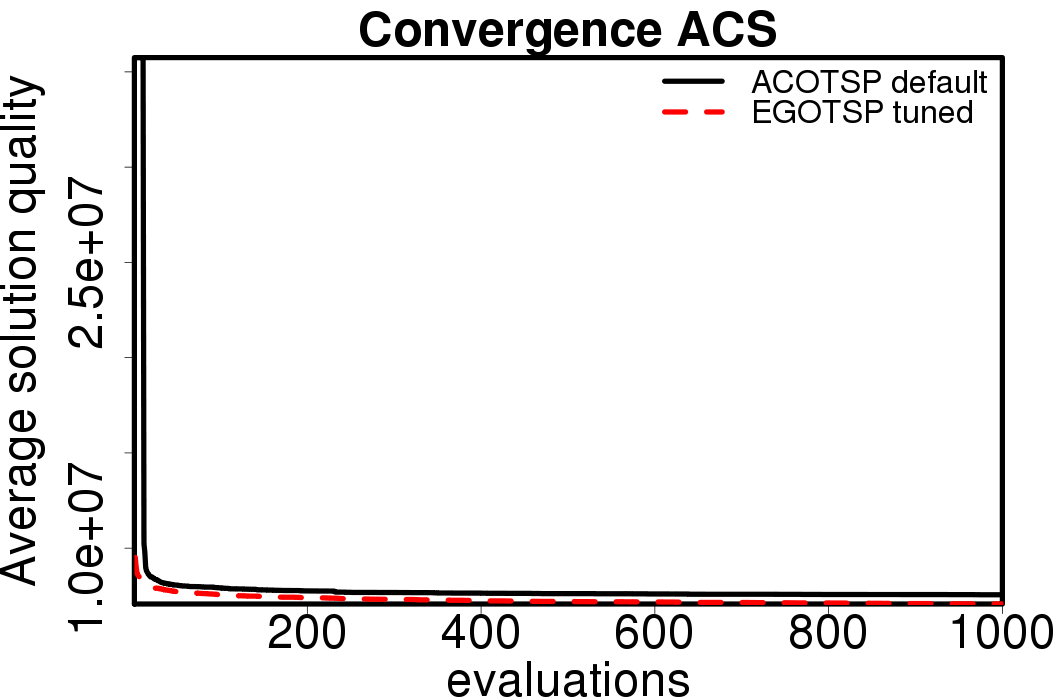
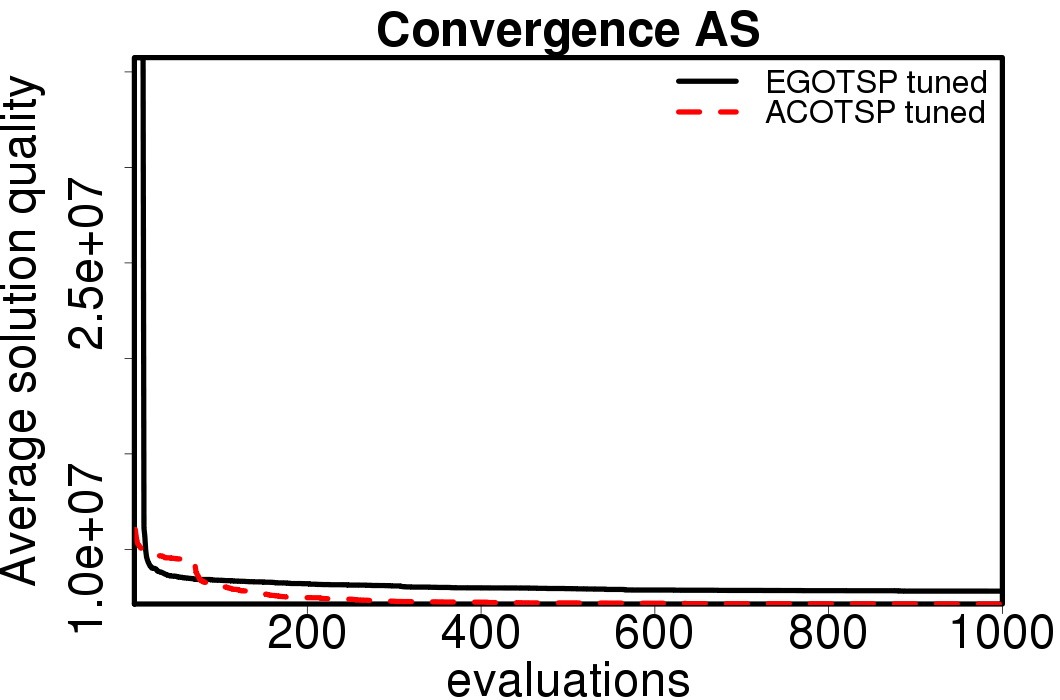
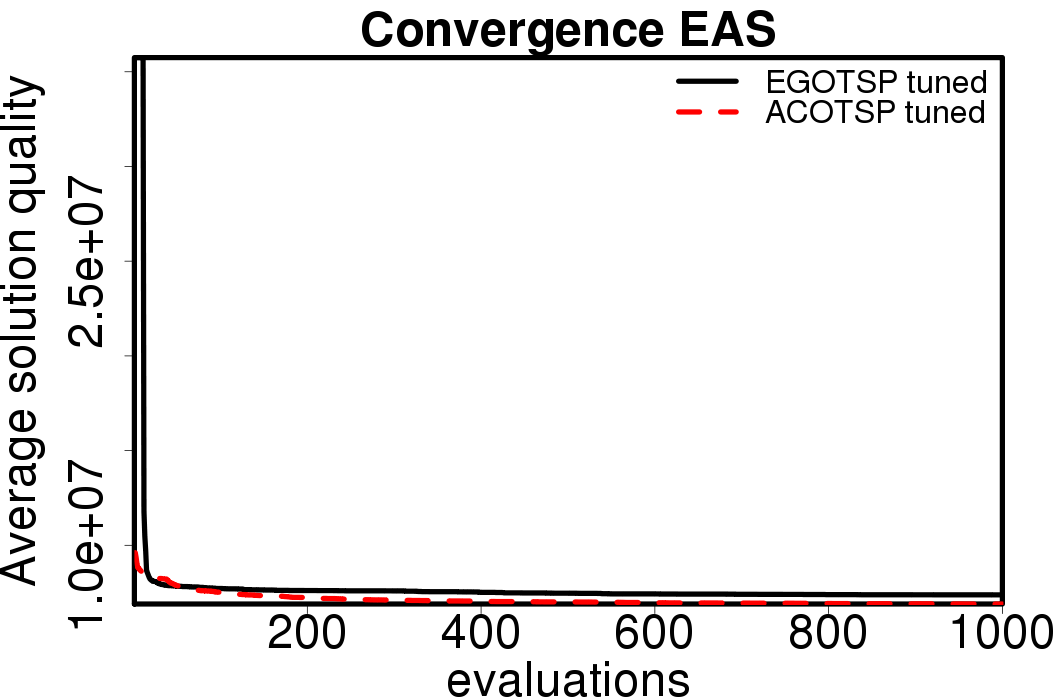
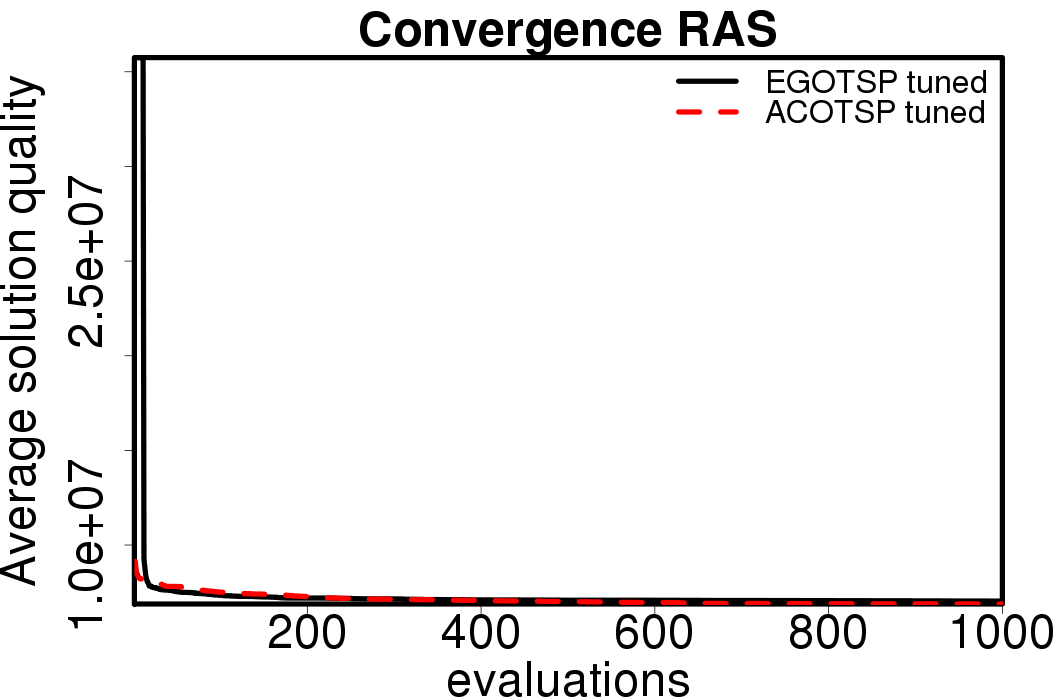
Average convergence graphs comparing the default/tuned settings by ACO algorithm:
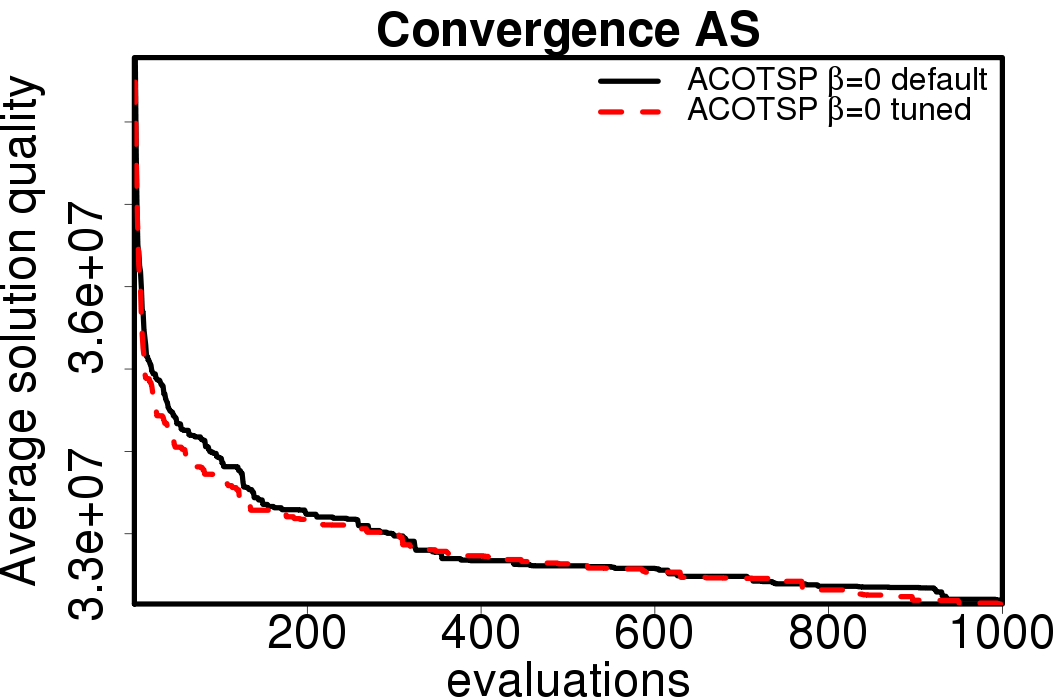 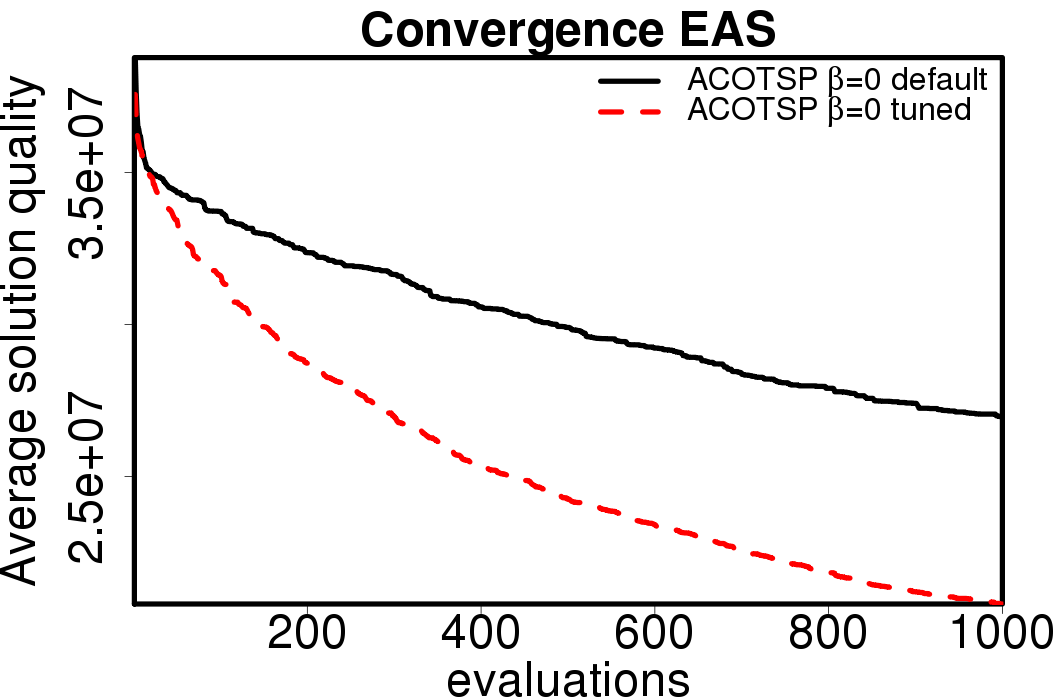 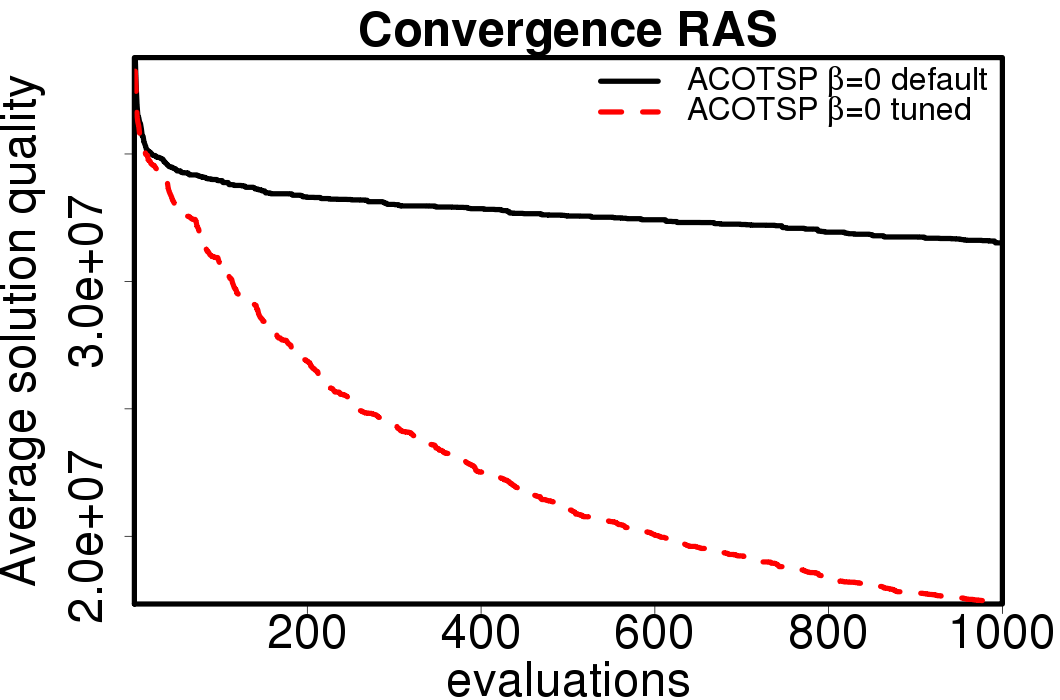 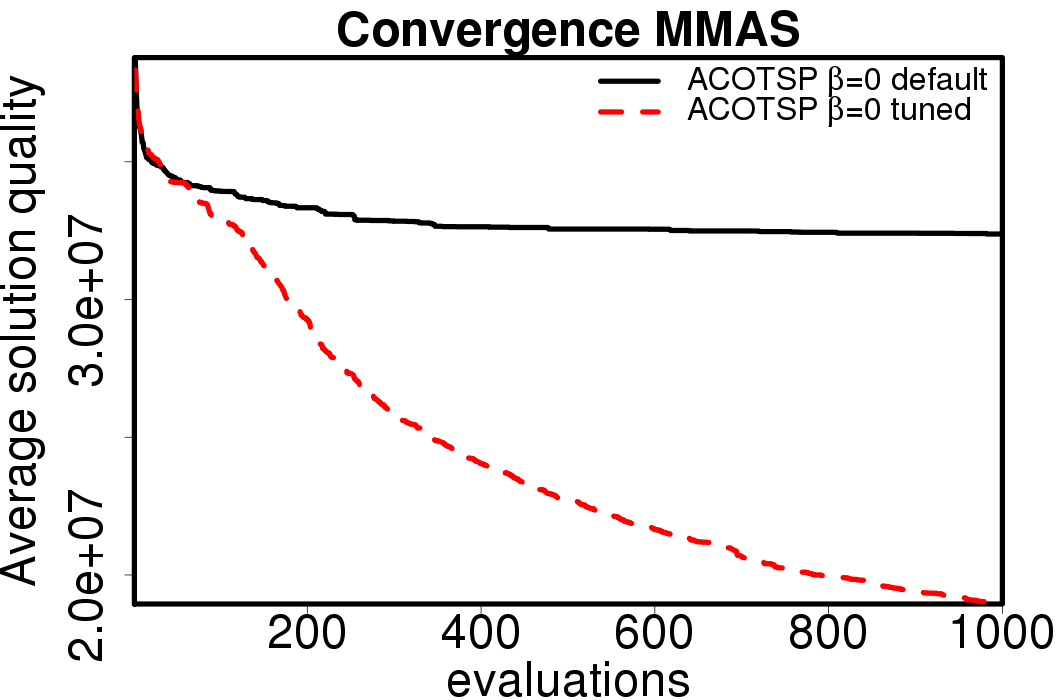 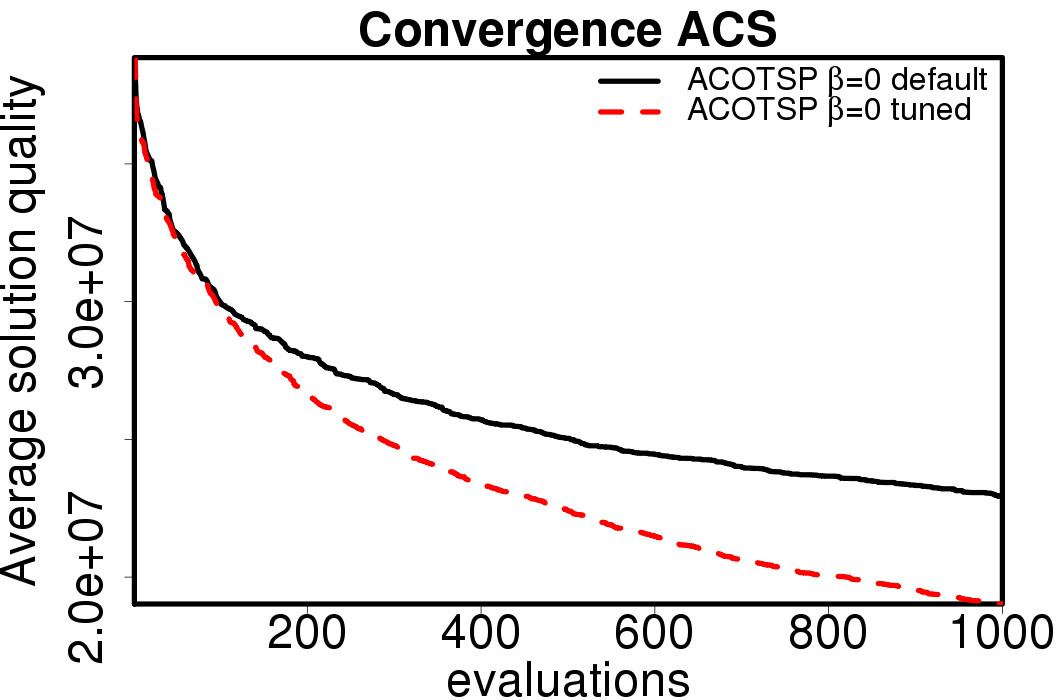
|
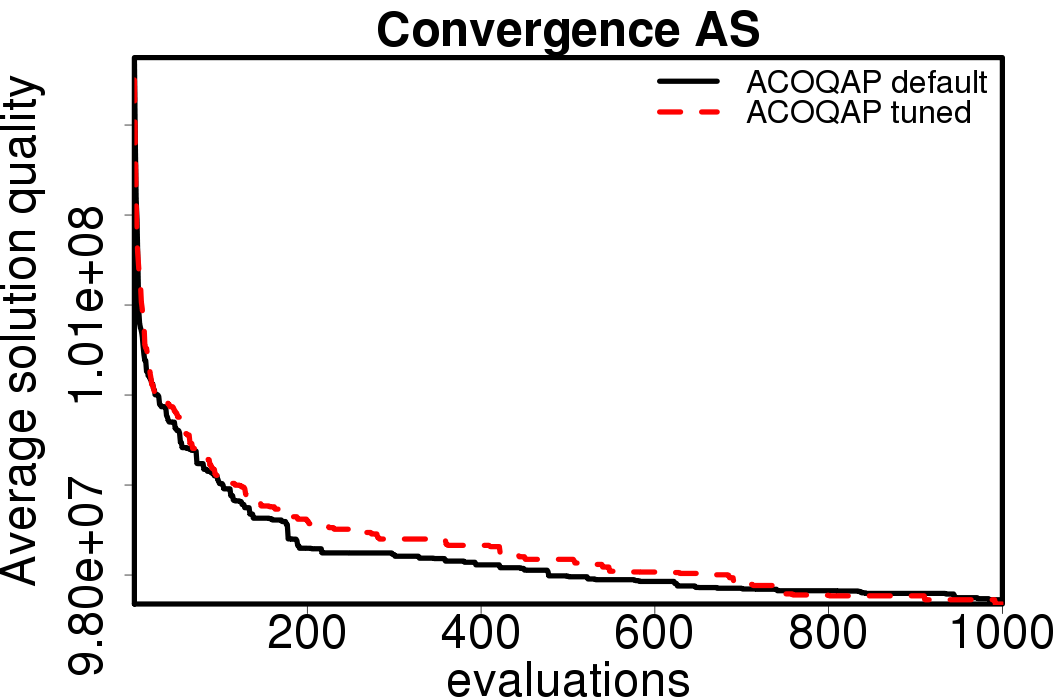 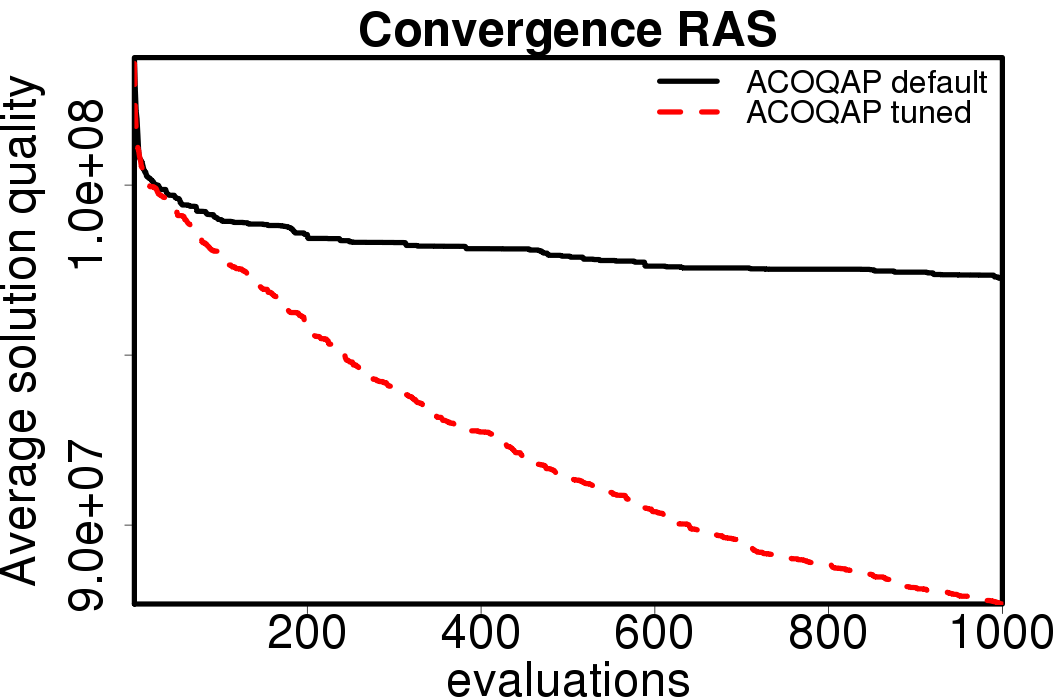 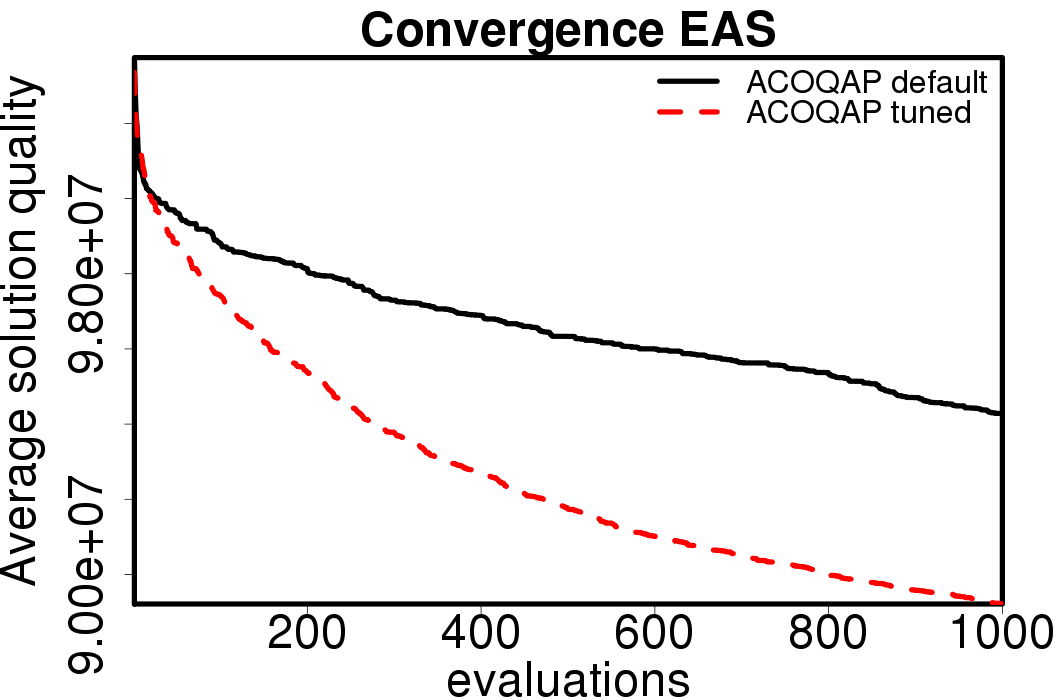 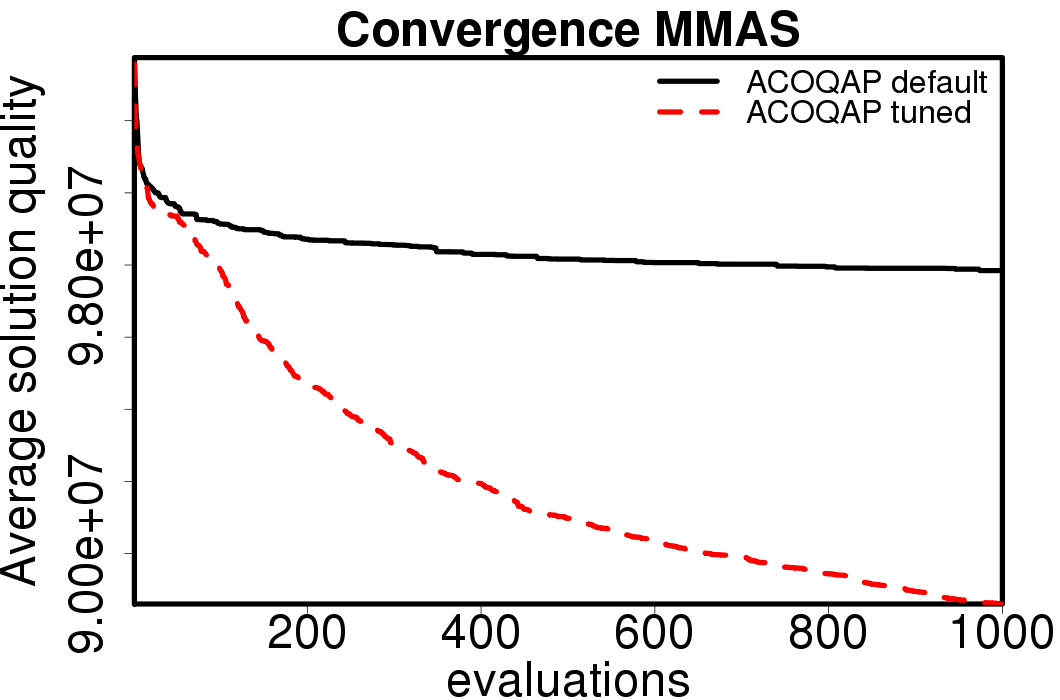 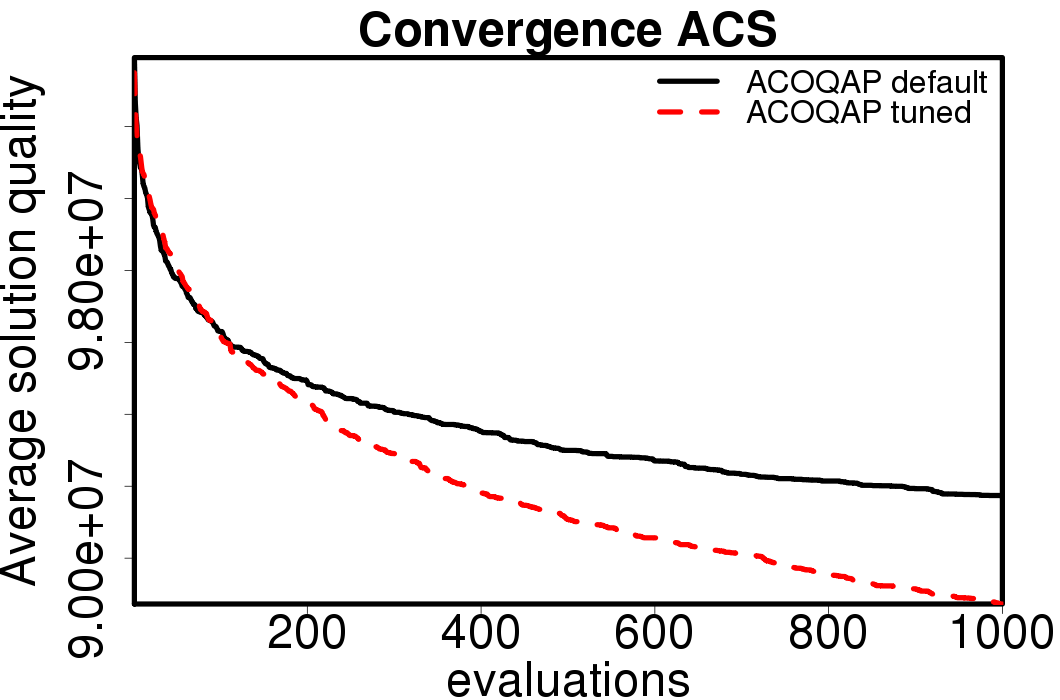
|
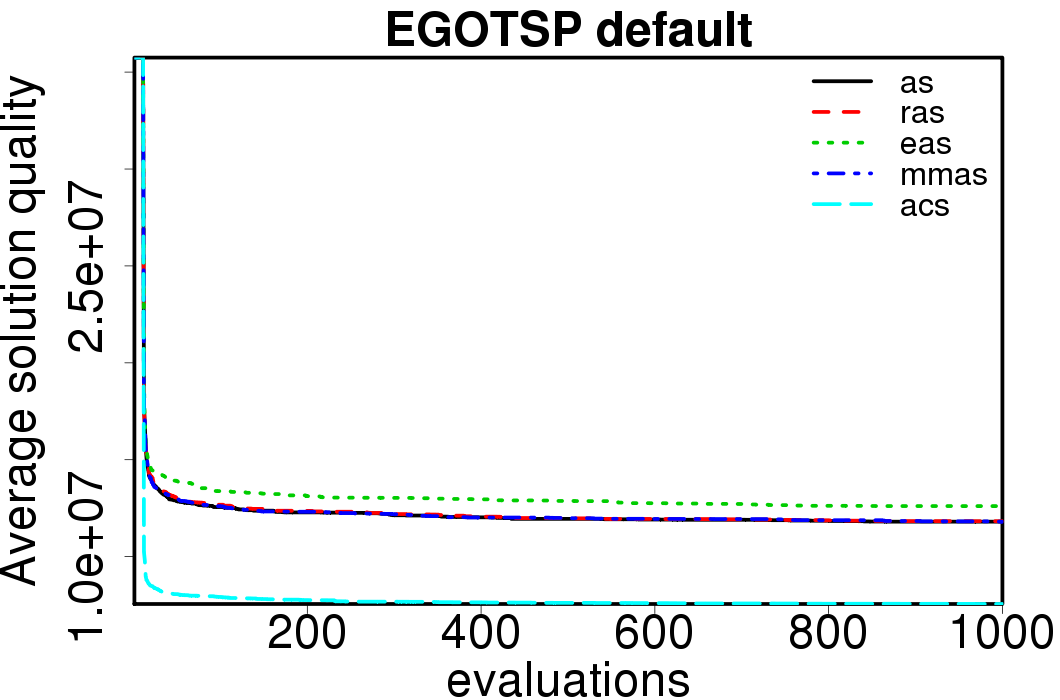
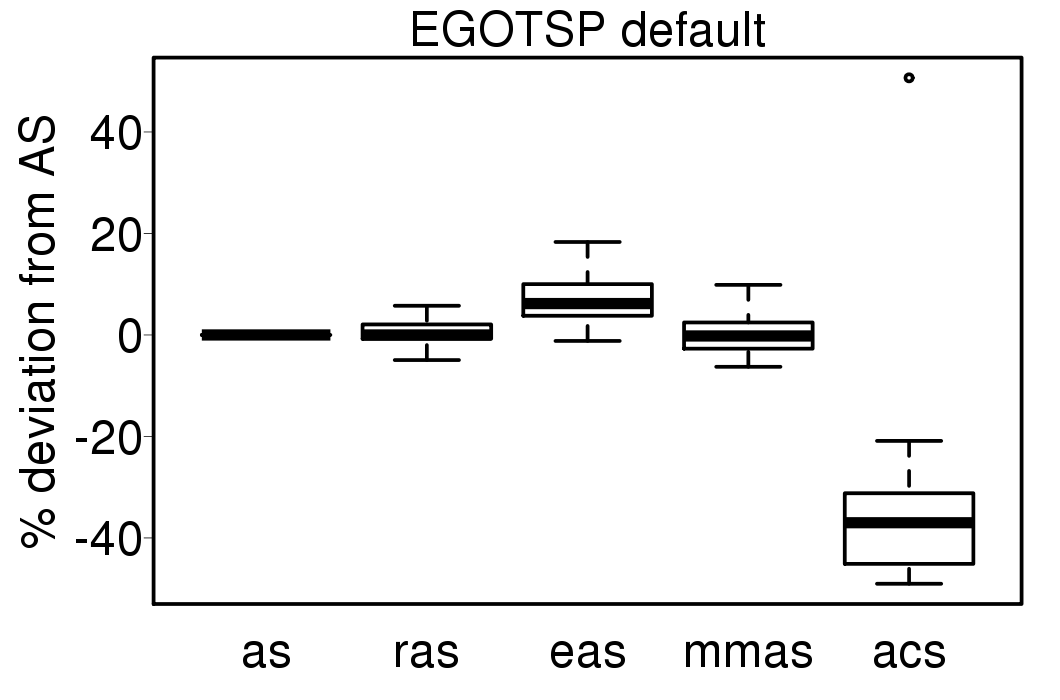
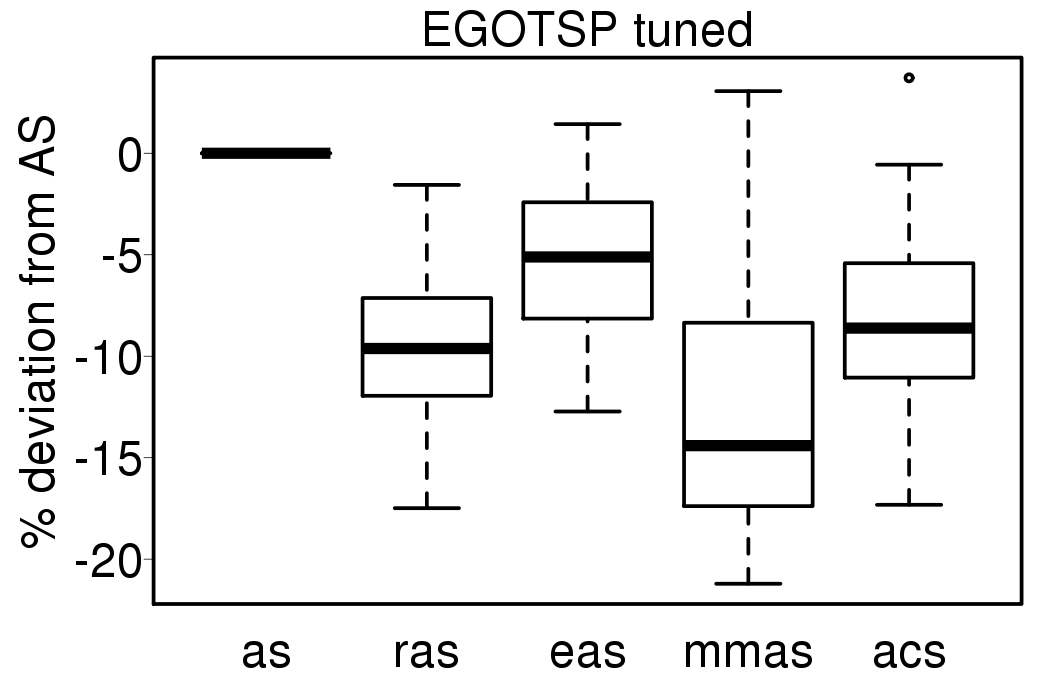
We execute the EGO algorithm using each of the ACO algorithms to search the Kriging model, the following plots show the relative performance of the EGO-ACO algorithms from EGO-AS:
 |
 |
The EGO-ACO algorithms don't show big difference in their results, excepting EGOTSP-ACS. Compared with the ACO algorithms applied directly on the problems.
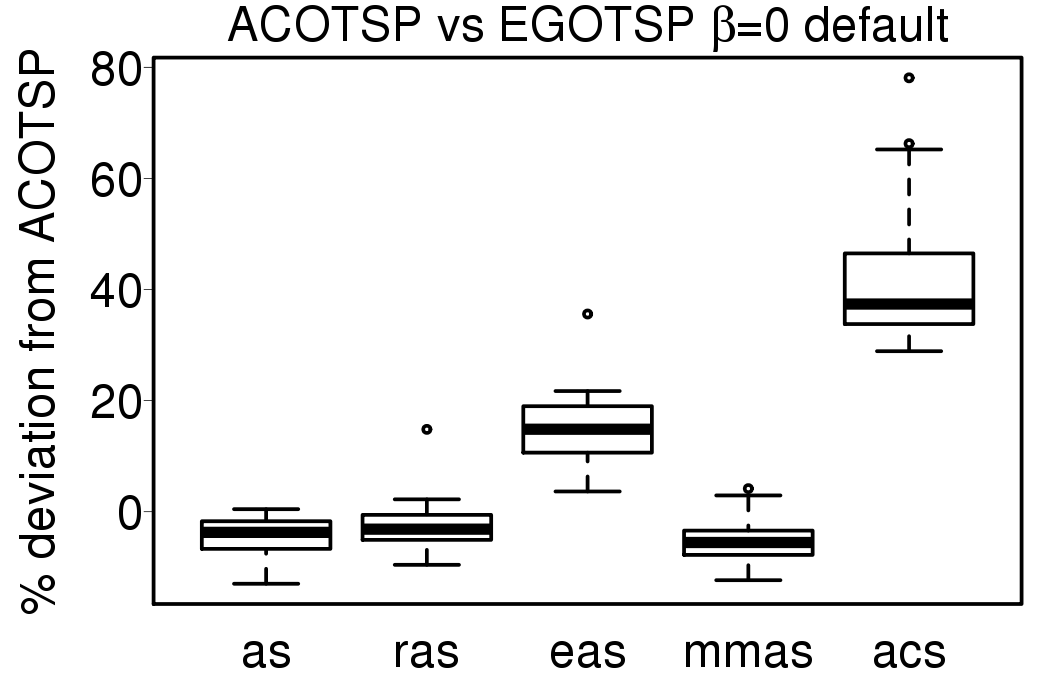 | 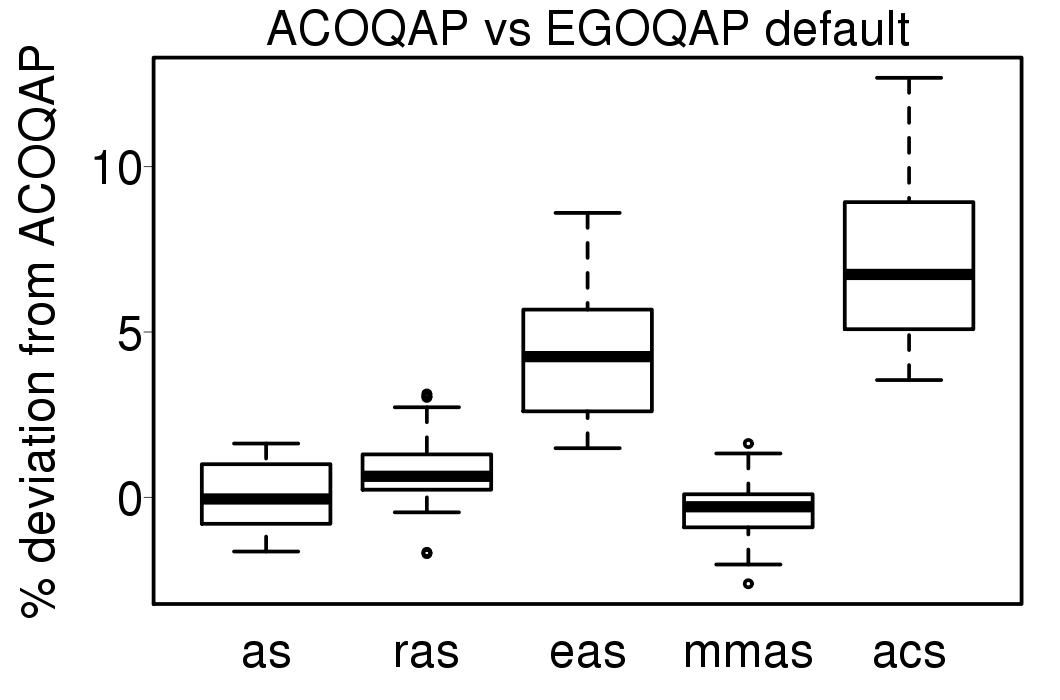 |
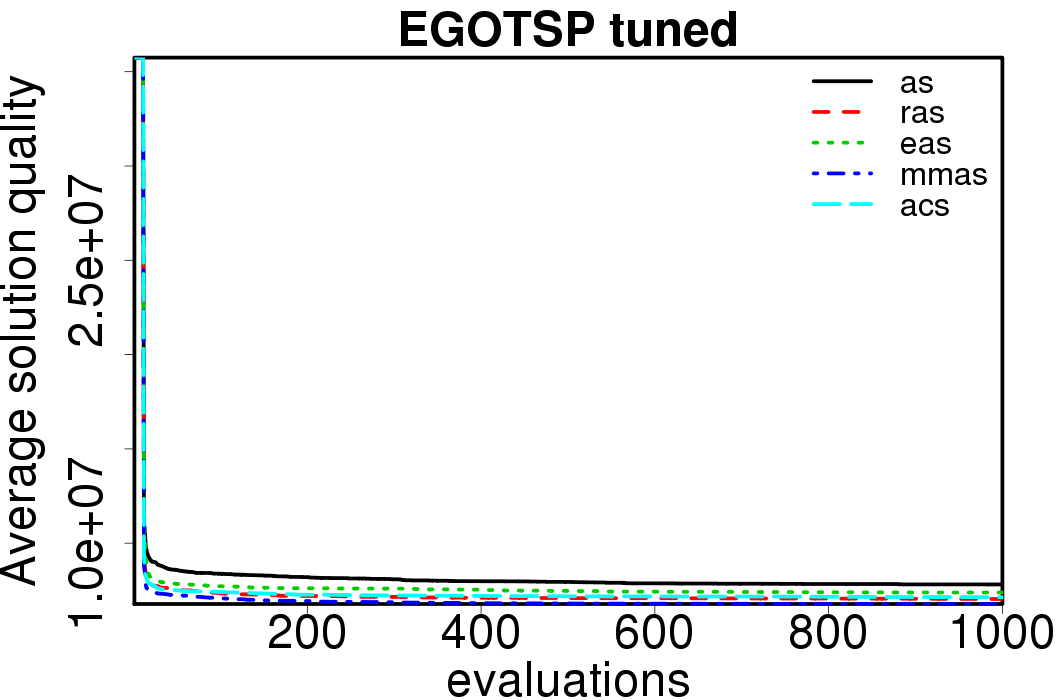
The following plots show the average convergence of the ACO and EGO-ACO algorithms on the different ACO algorithms.
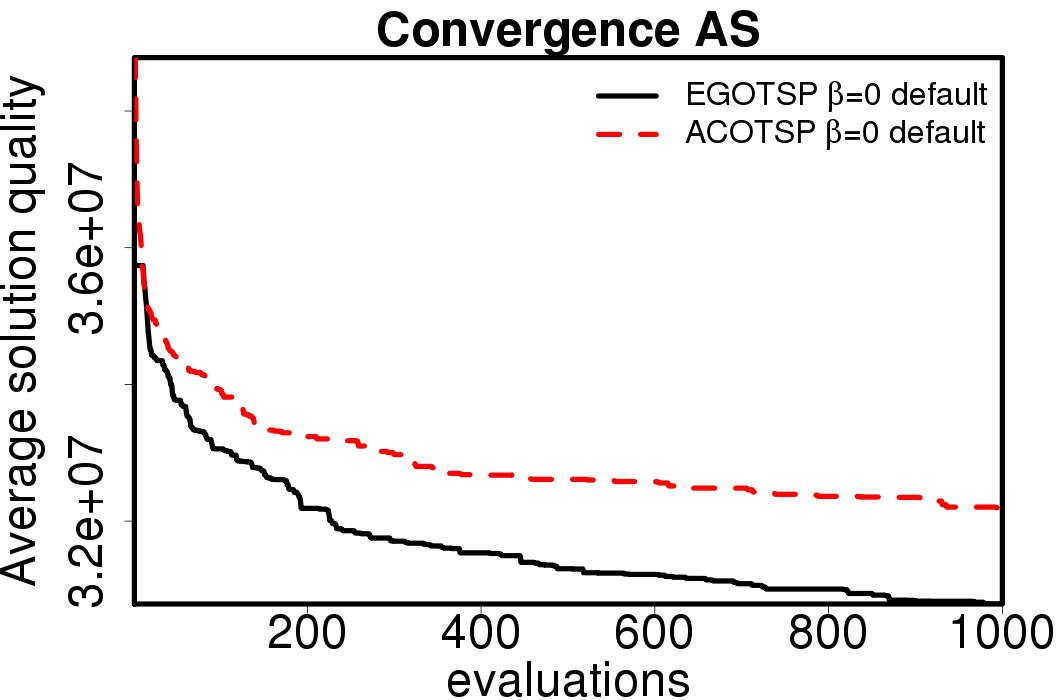 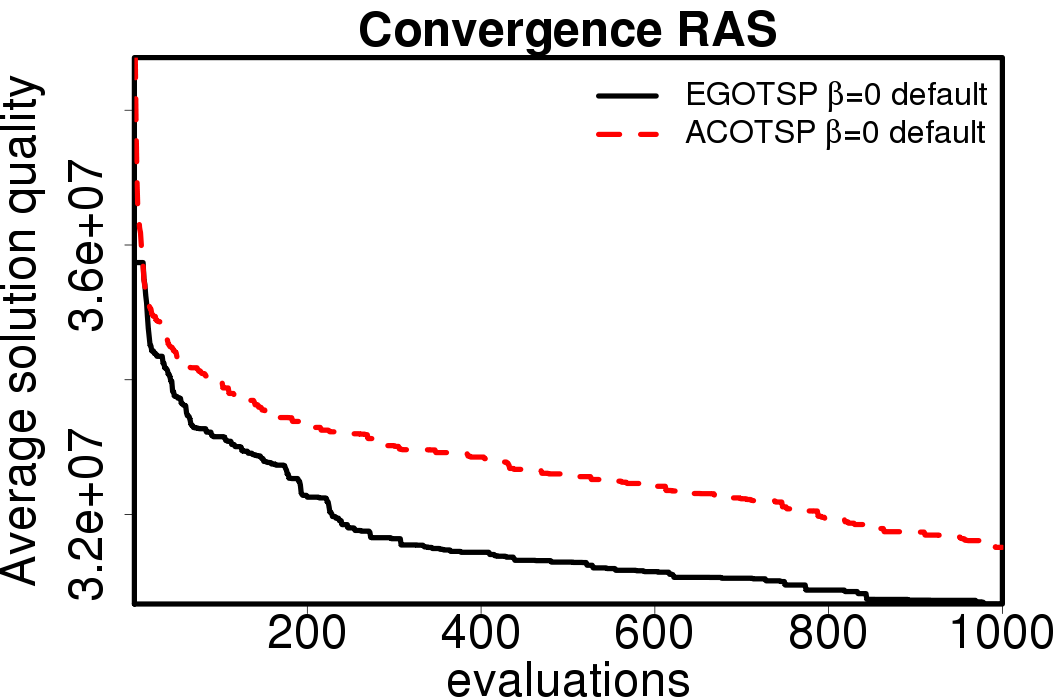 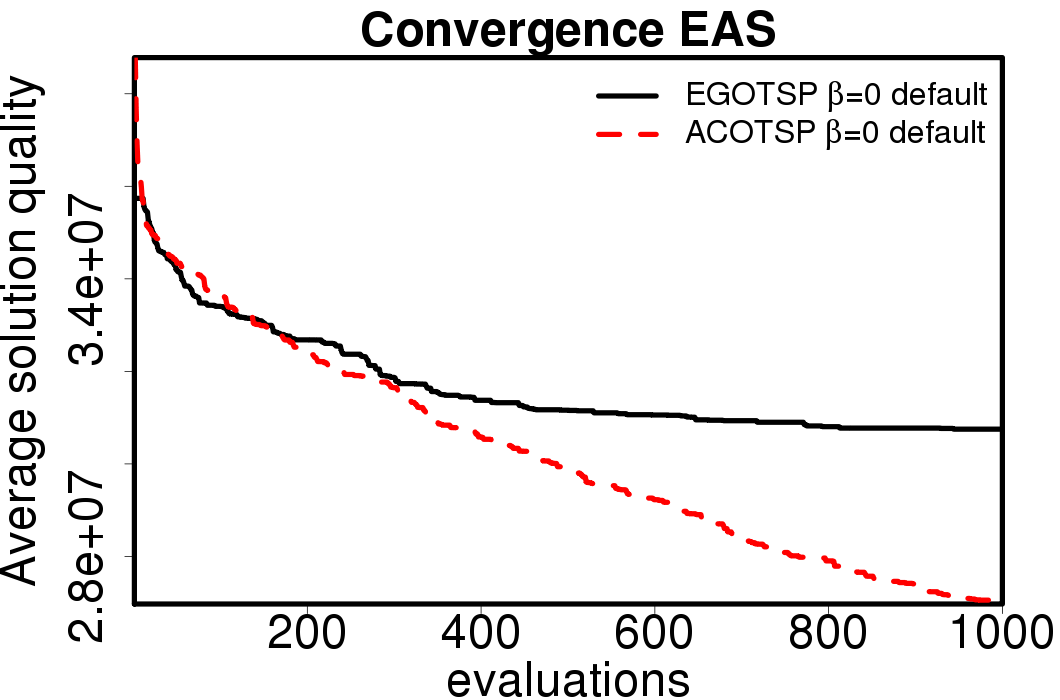 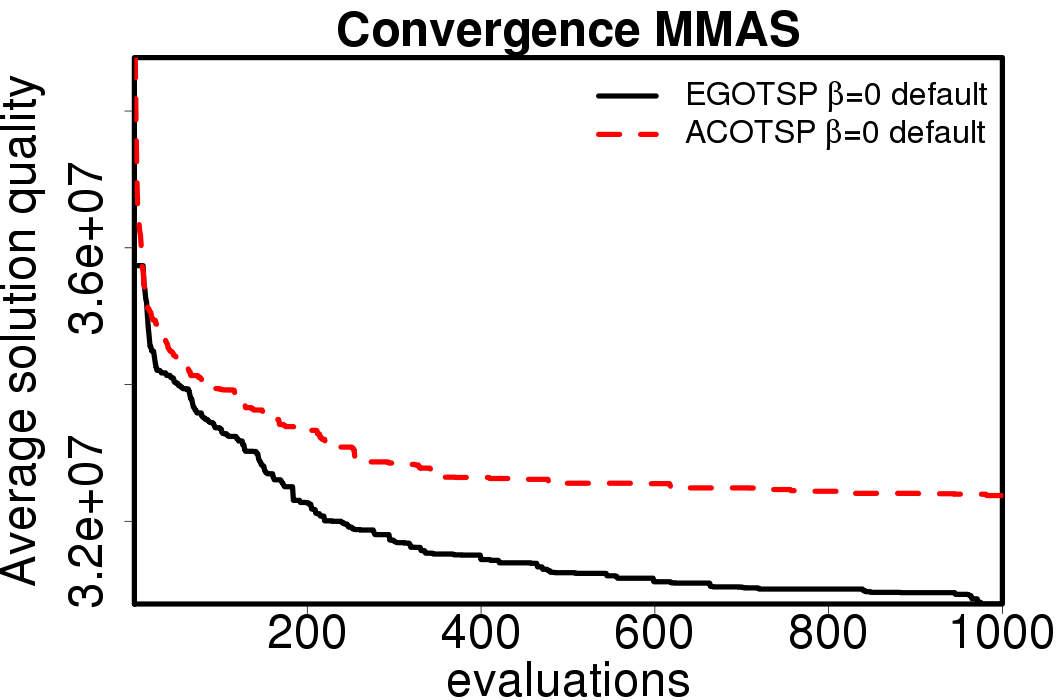 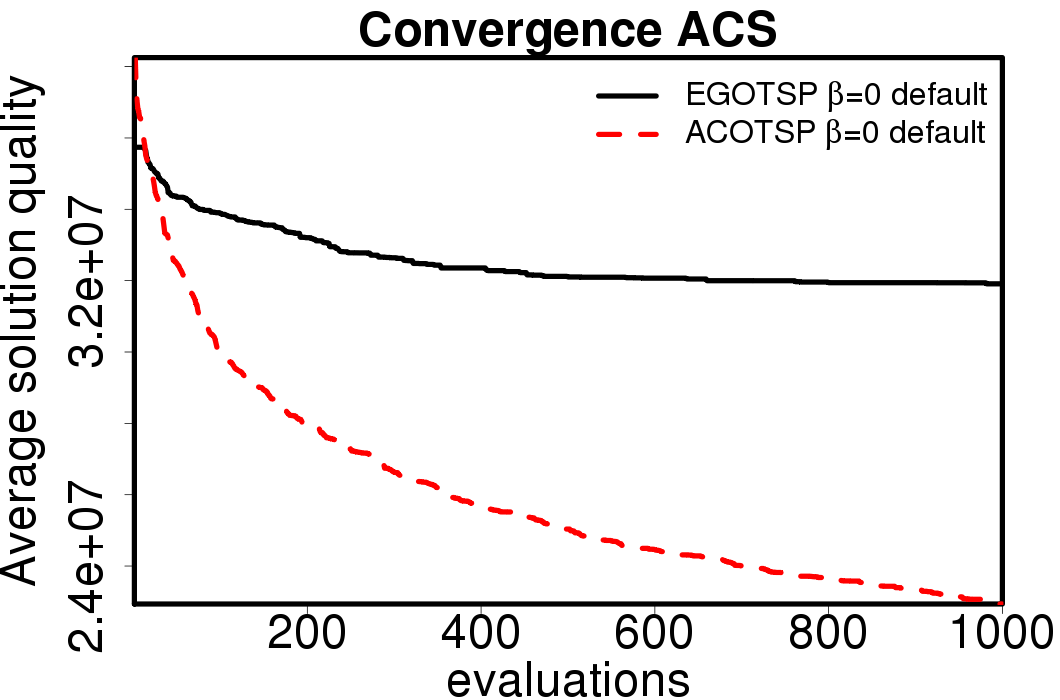
|
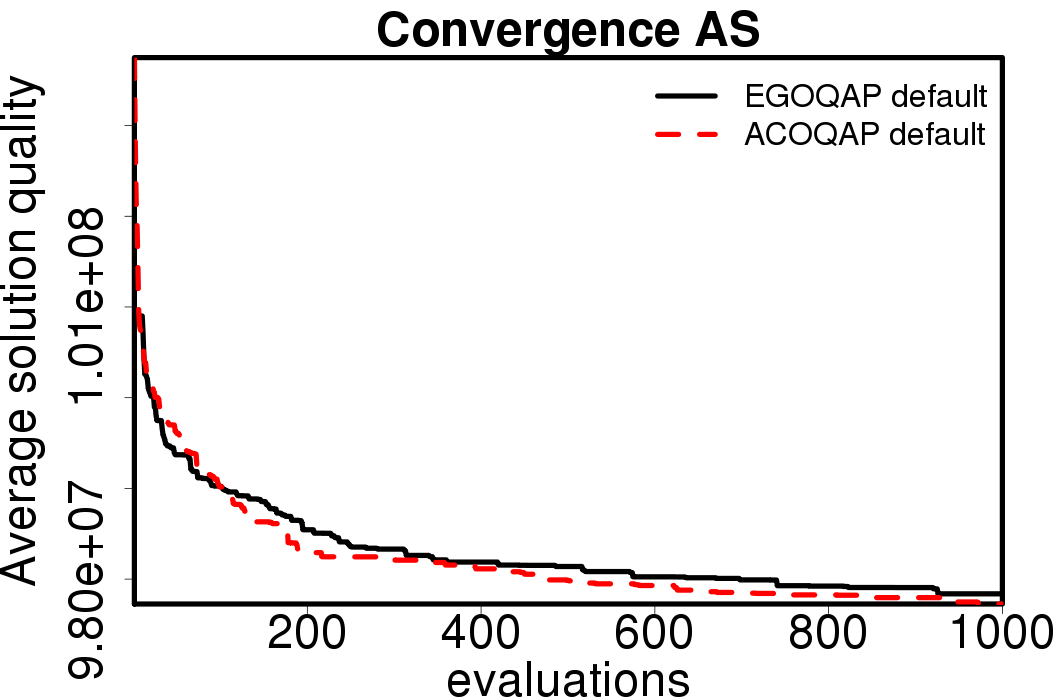 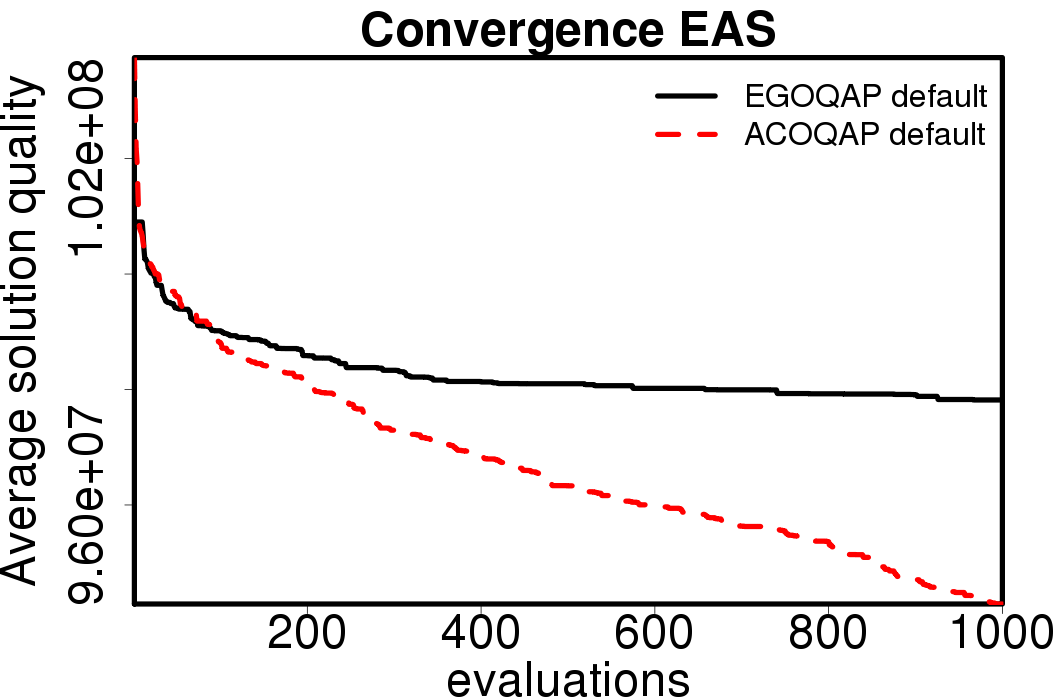 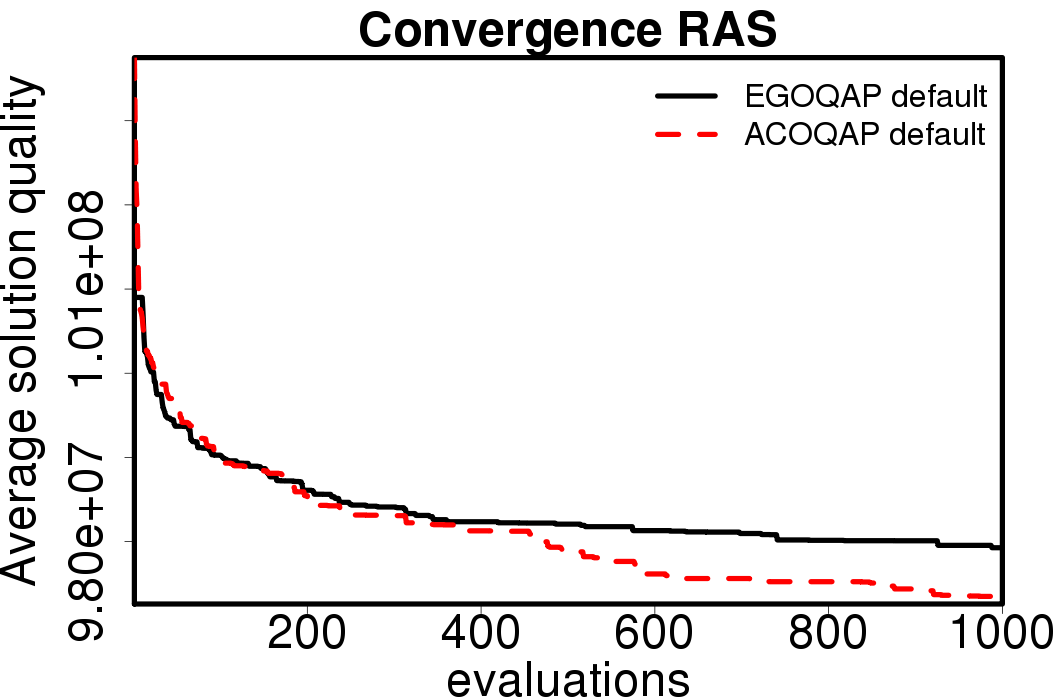 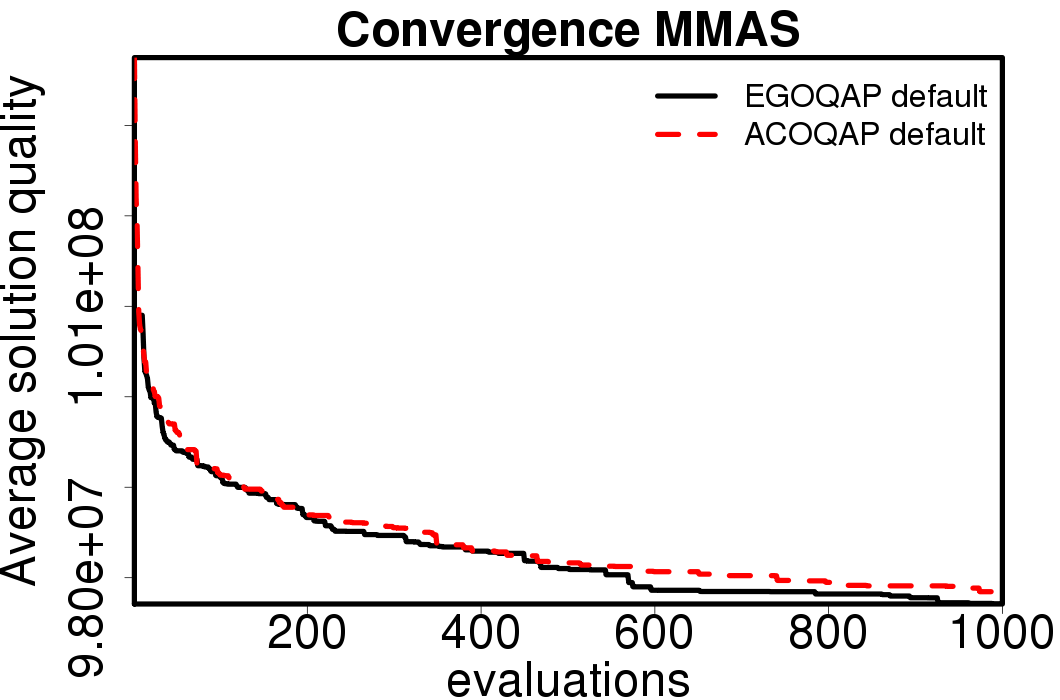 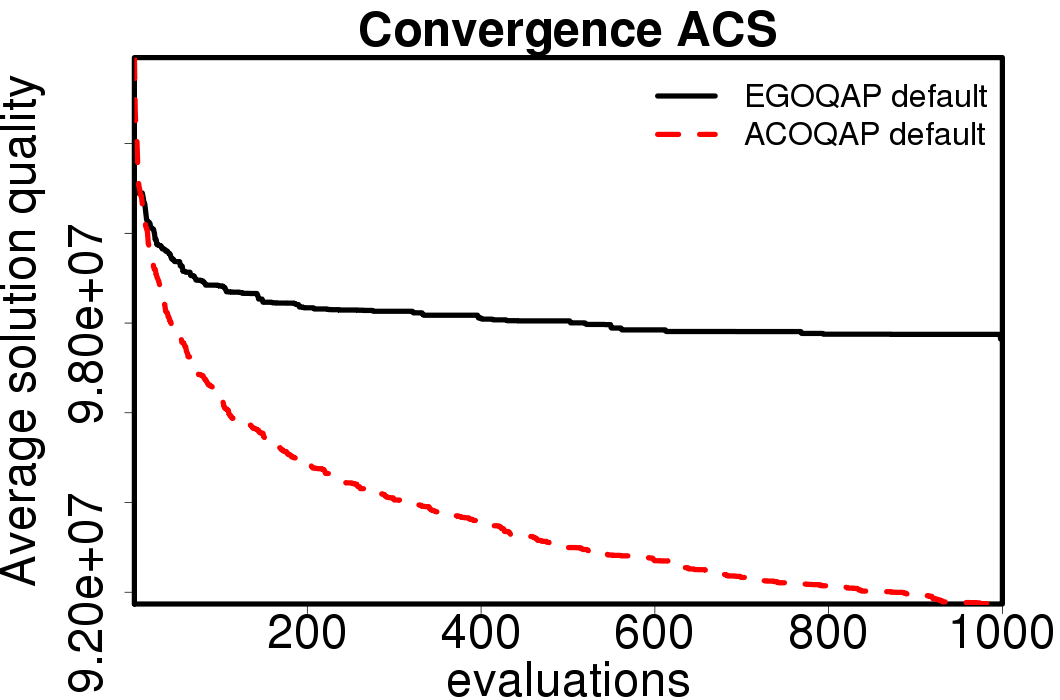
|
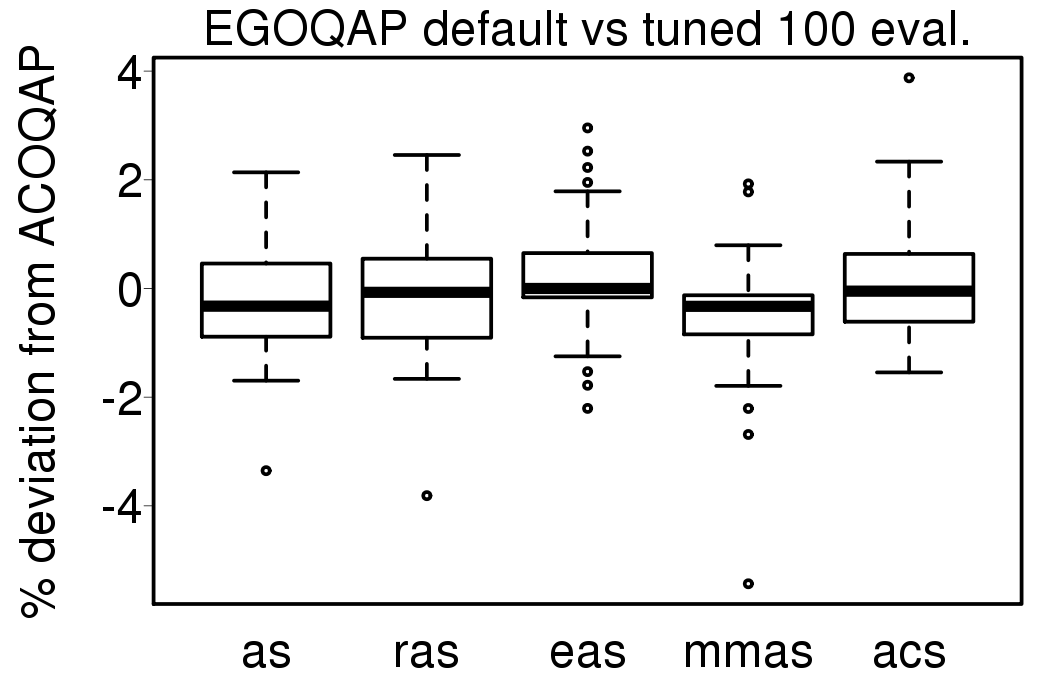
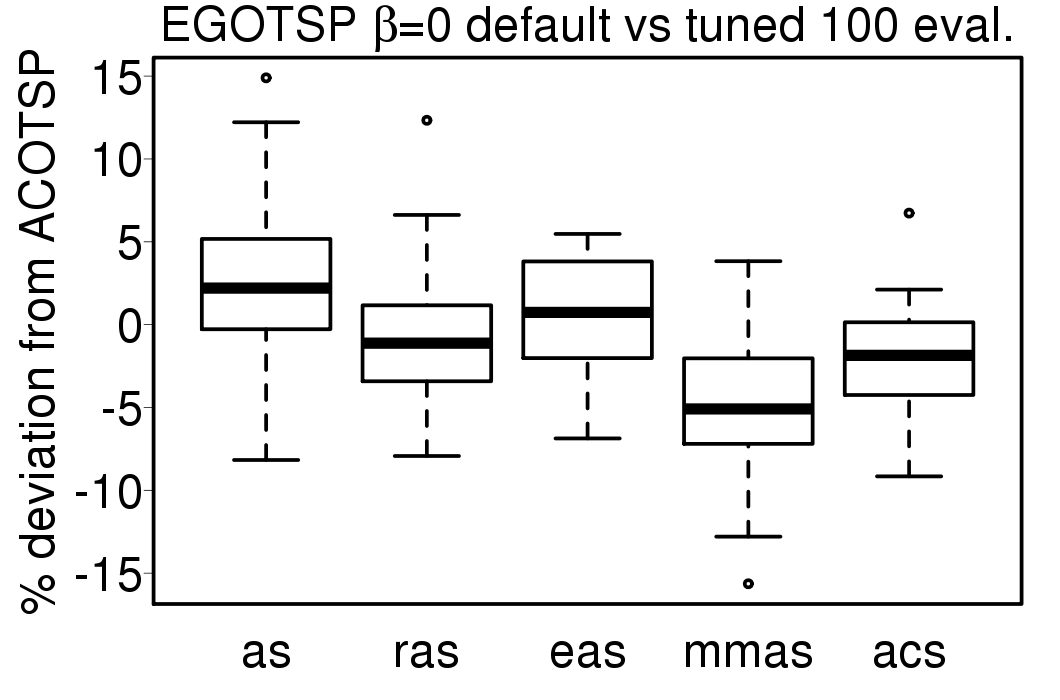
We used the tuned settings in Table 3 for the EGO-ACO algorithms, the average solution quality deviation of the tuned settings results from the default settings results are shown in these plots:
|
|
Only EGOTSP-MMAS, EGOTSP-RAS and EGOQAP-EAS have statistically improved results. The relative percentage deviation from EGO-AS of the EGO-ACO algorithms is shown in the following plots:
 |
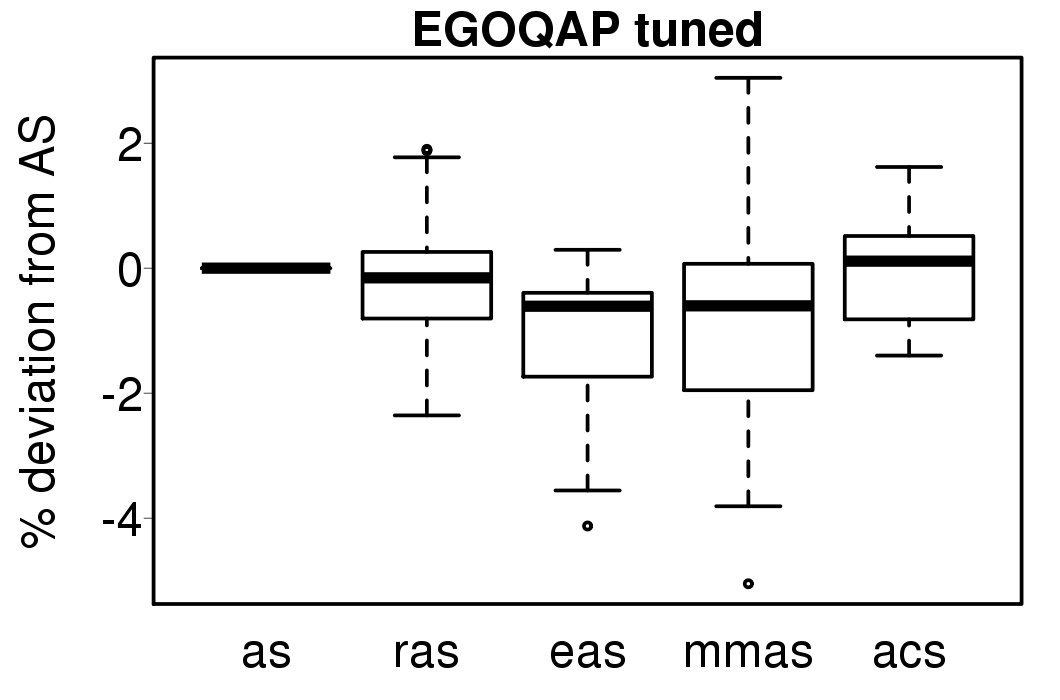  |
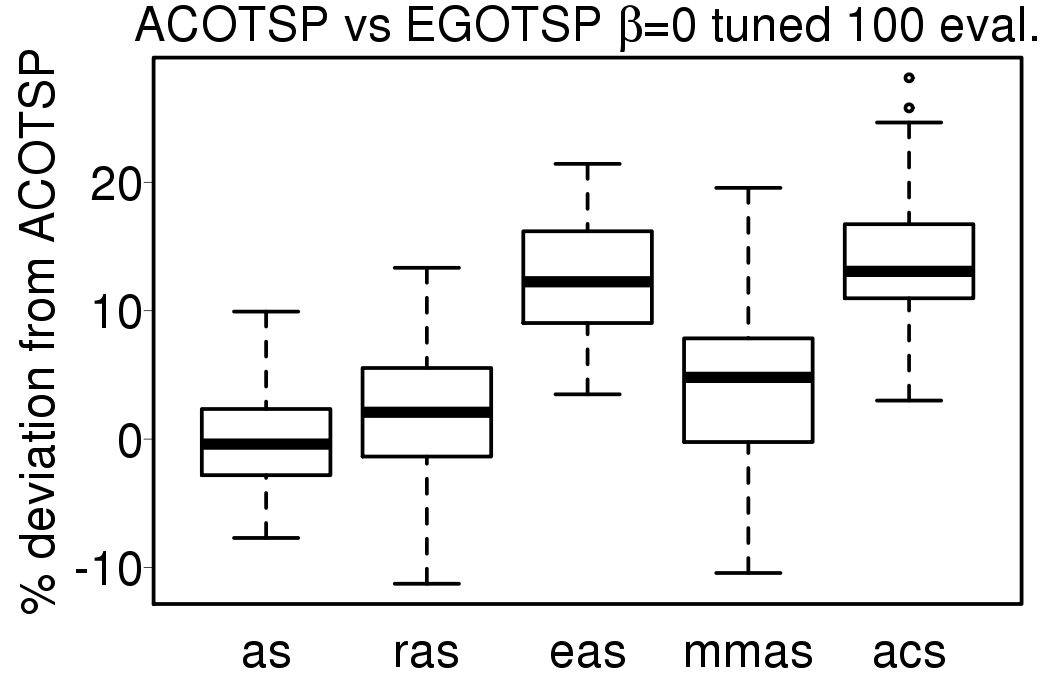
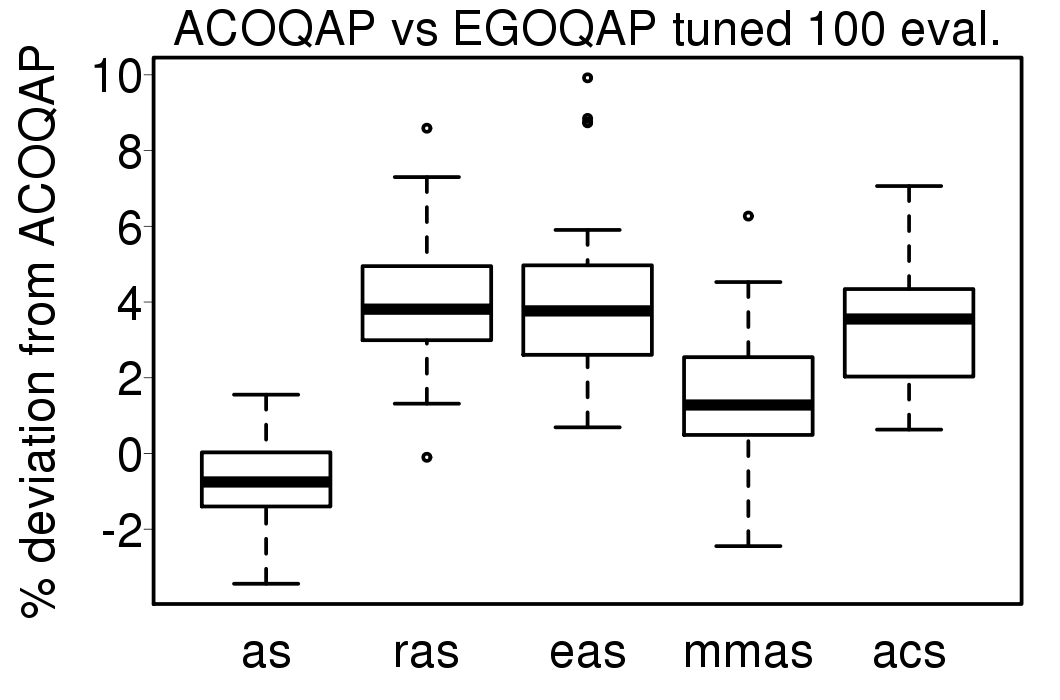
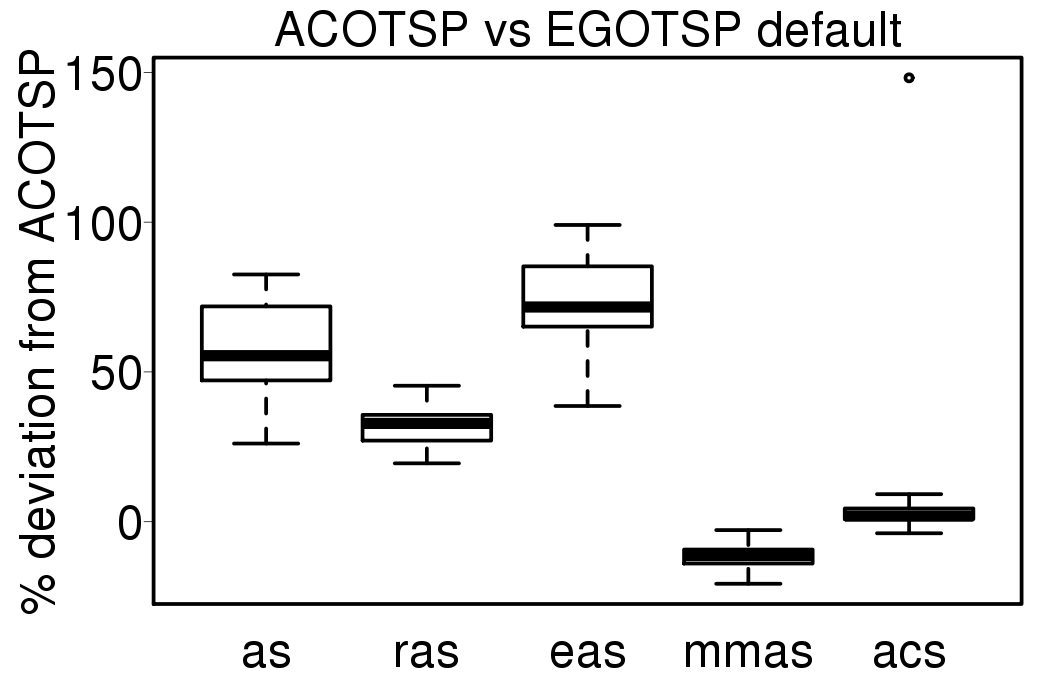
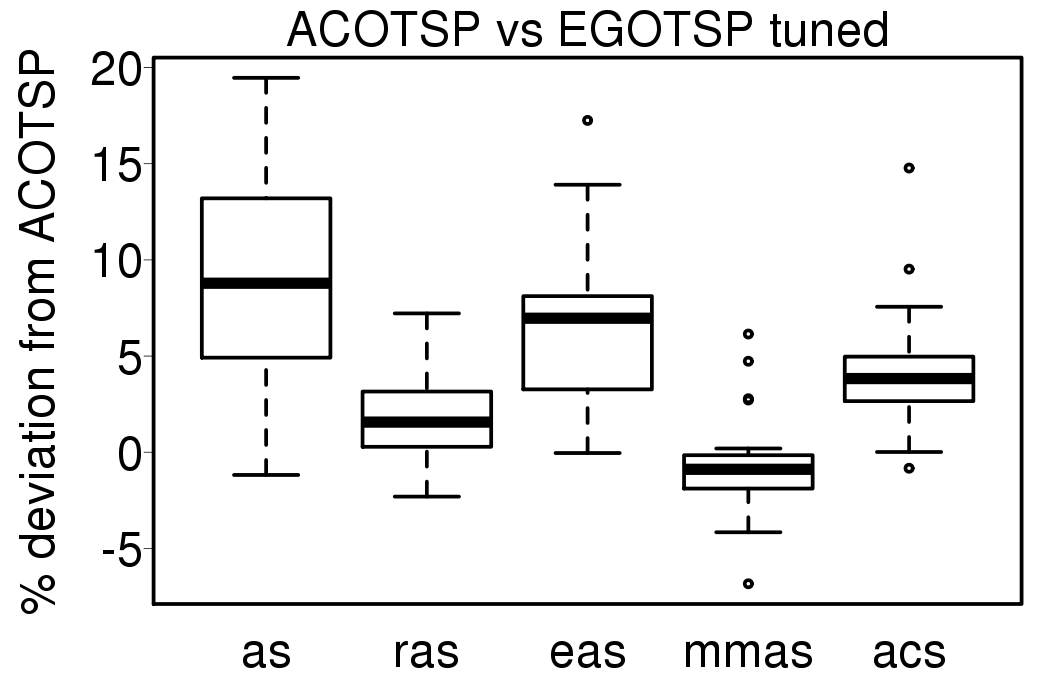
The comparisons between the EGO-ACO results using the tuned settings and the ACO algorithms using the same tuned settings are given in the following plots:
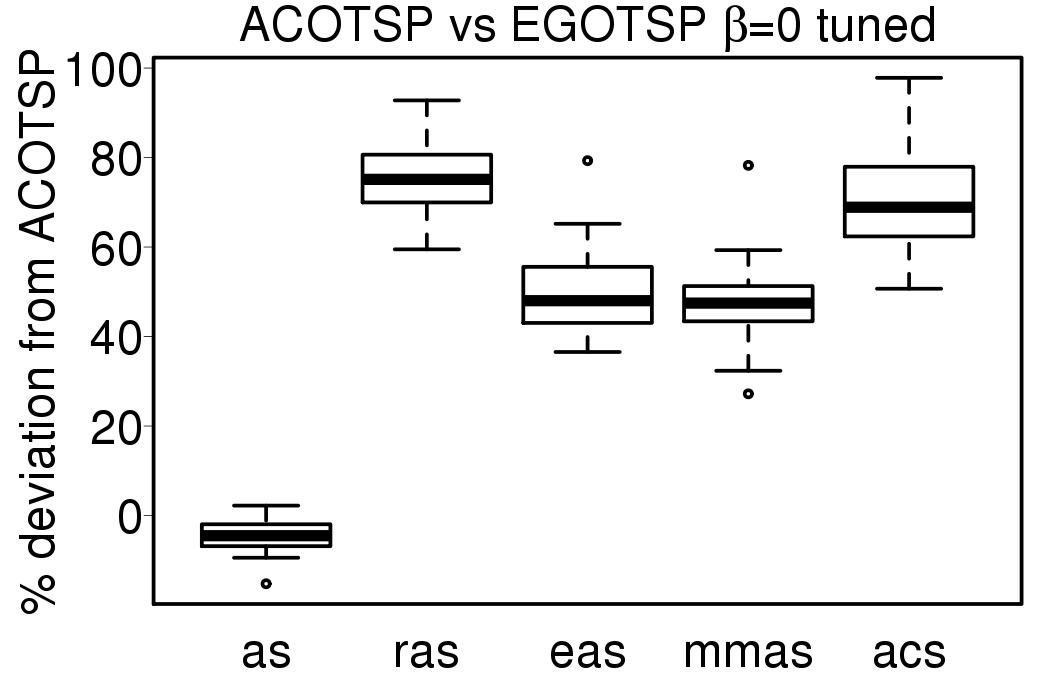
|
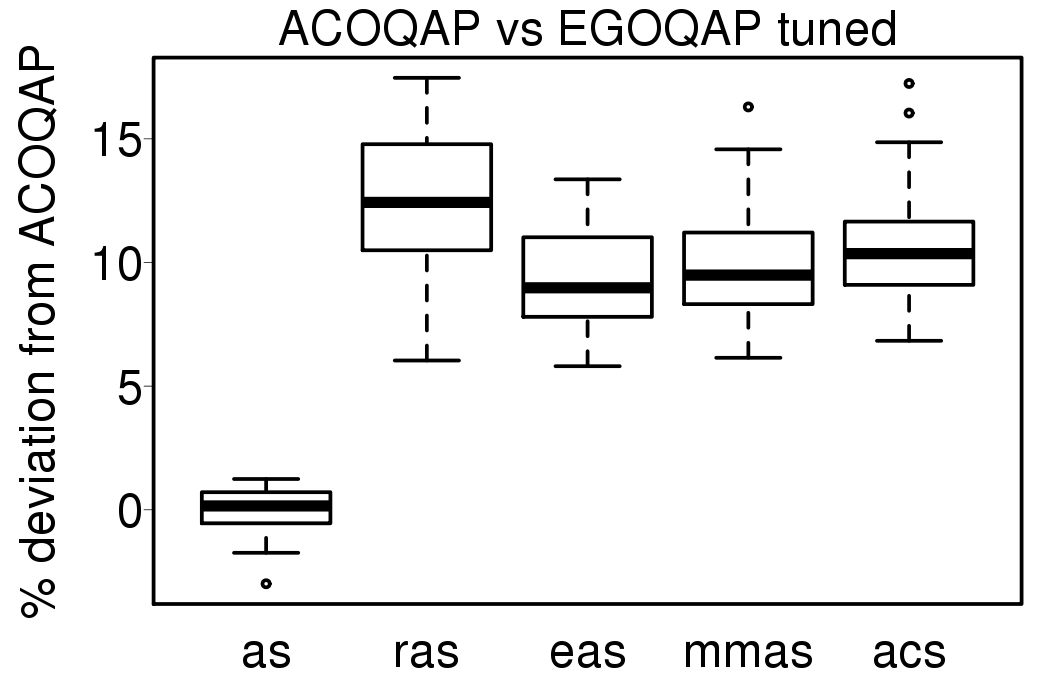
|
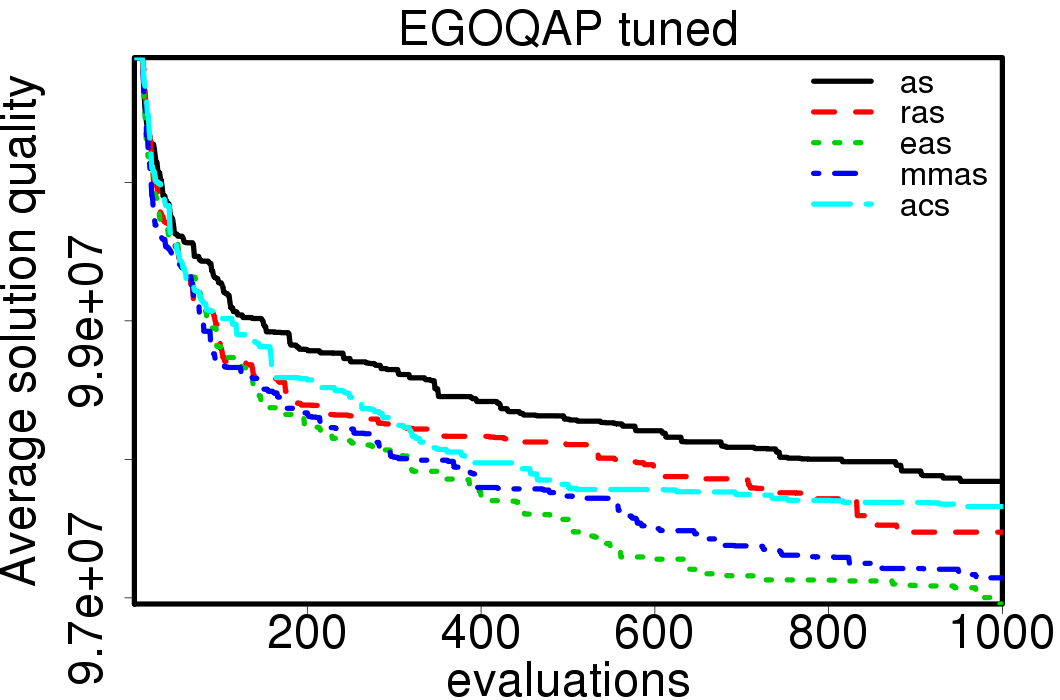
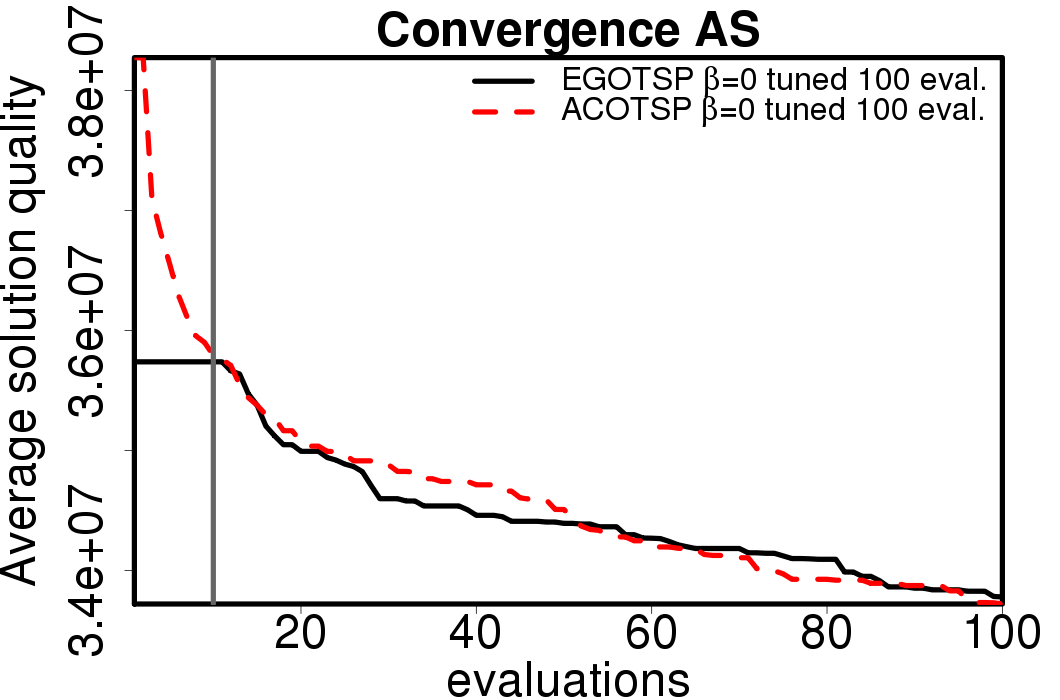
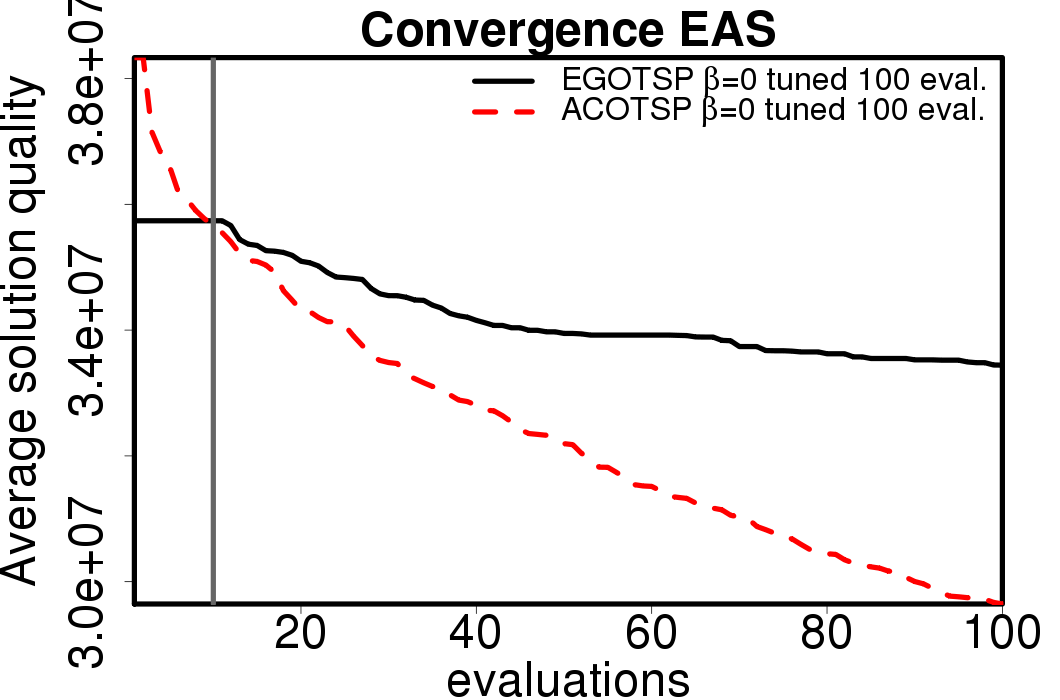
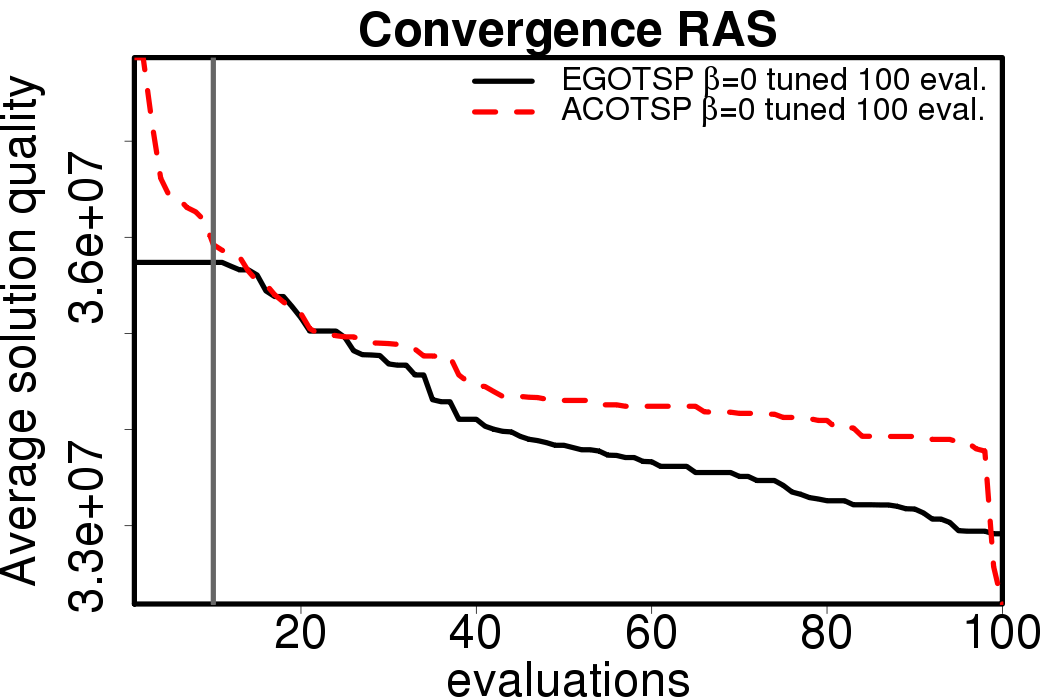
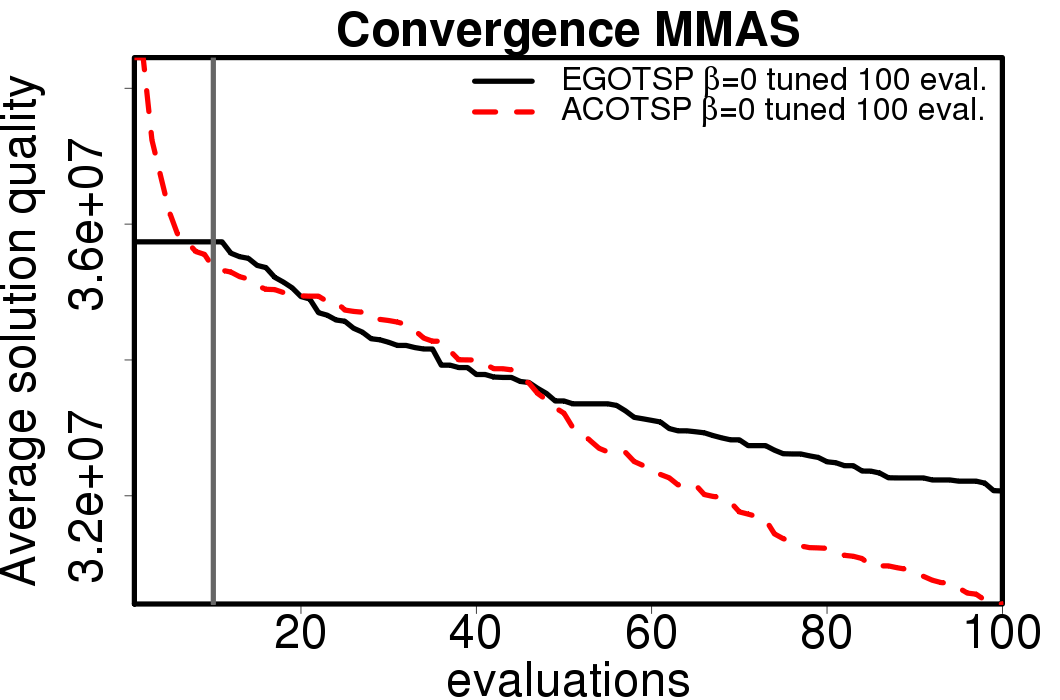
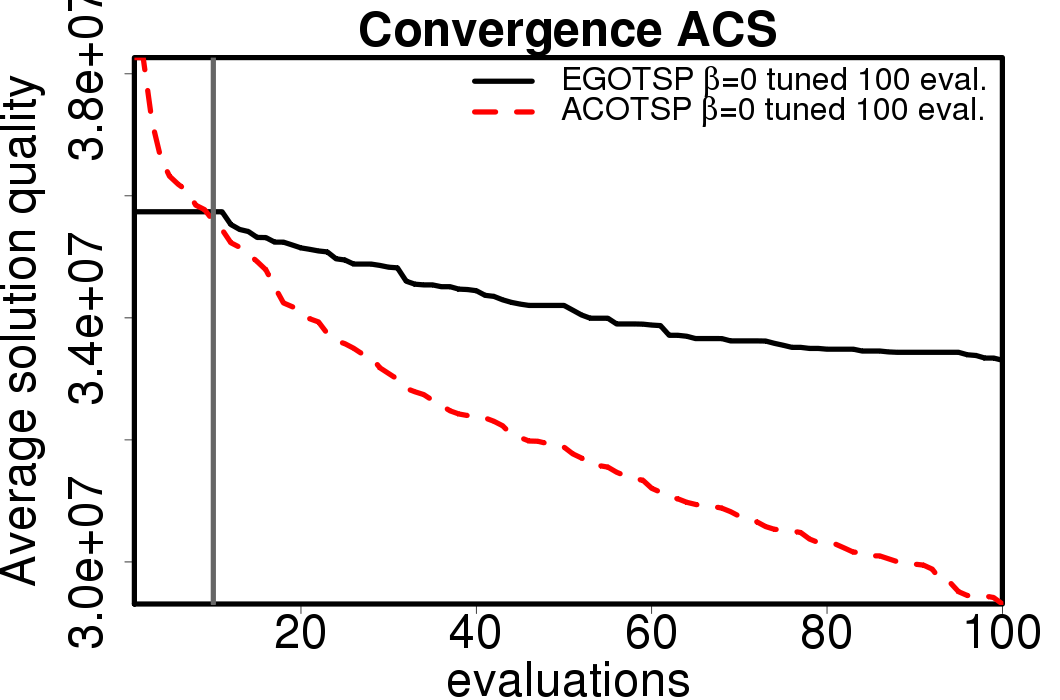
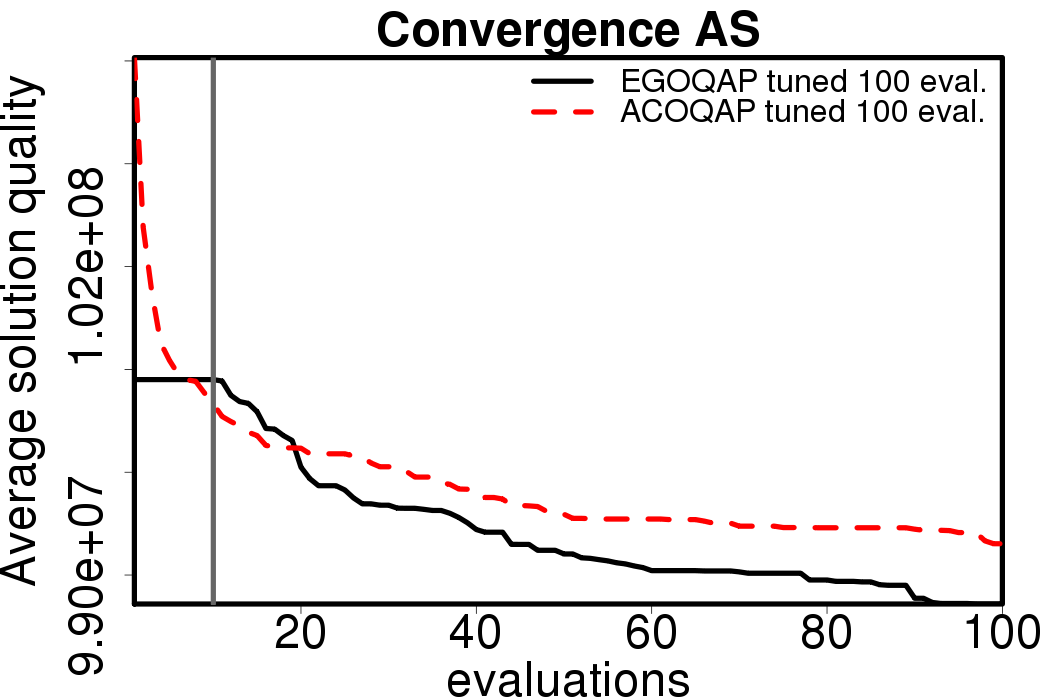
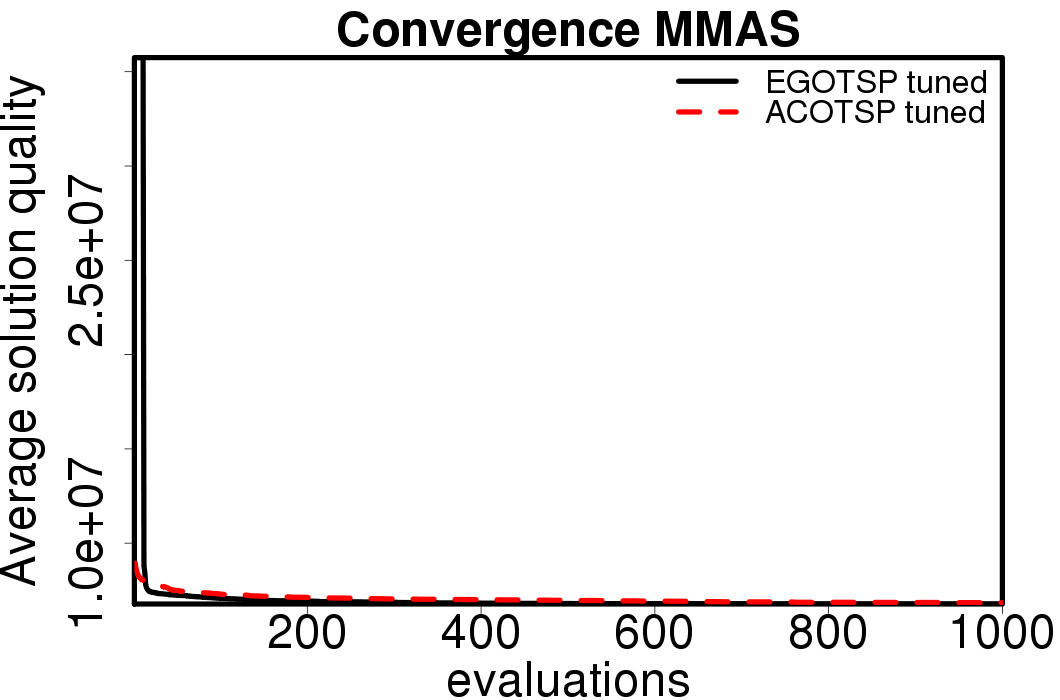
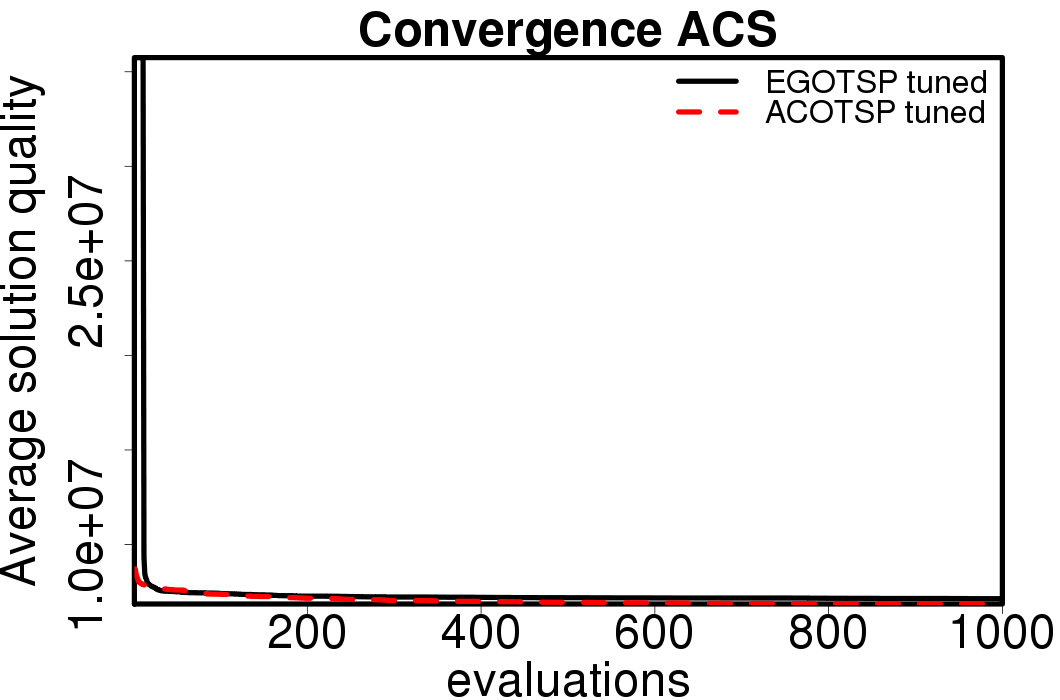
The average convergence is depicted in:
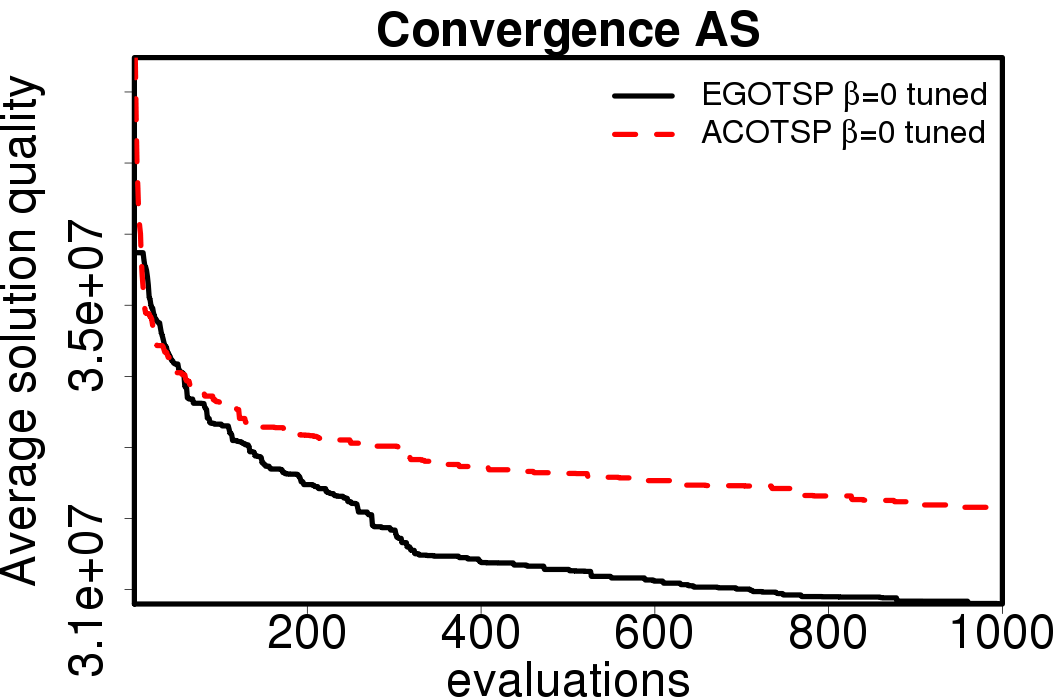 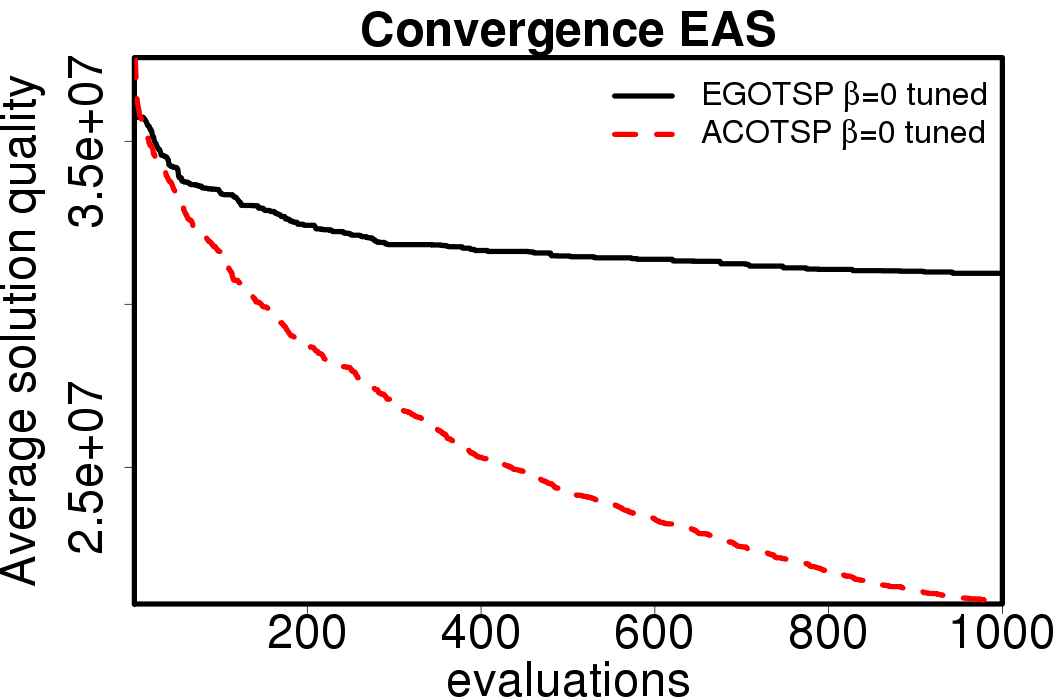 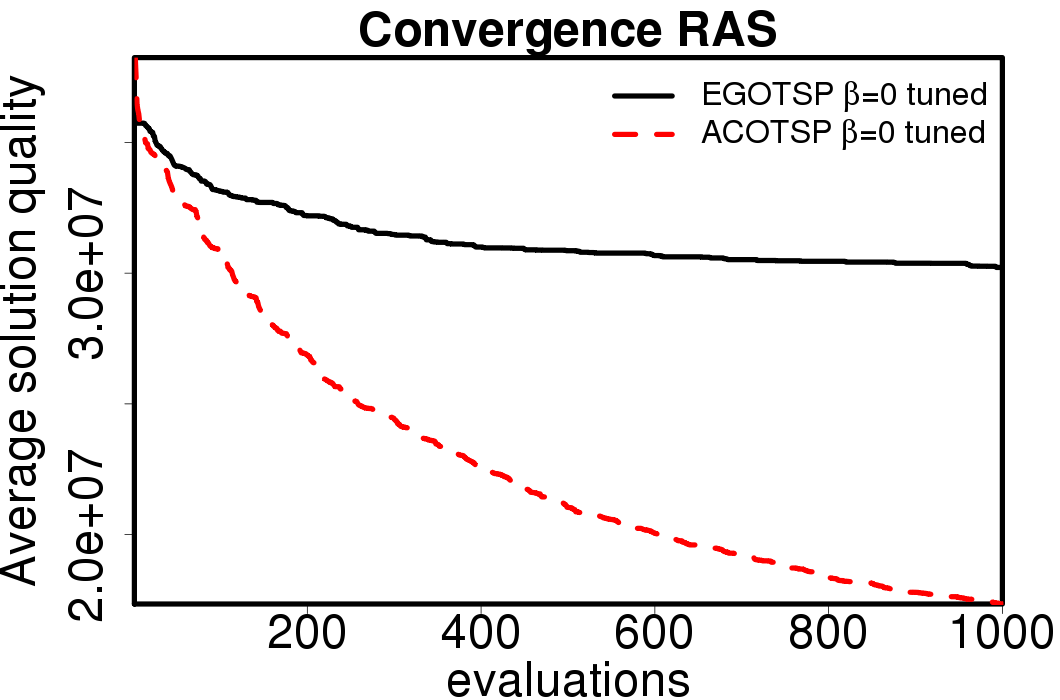 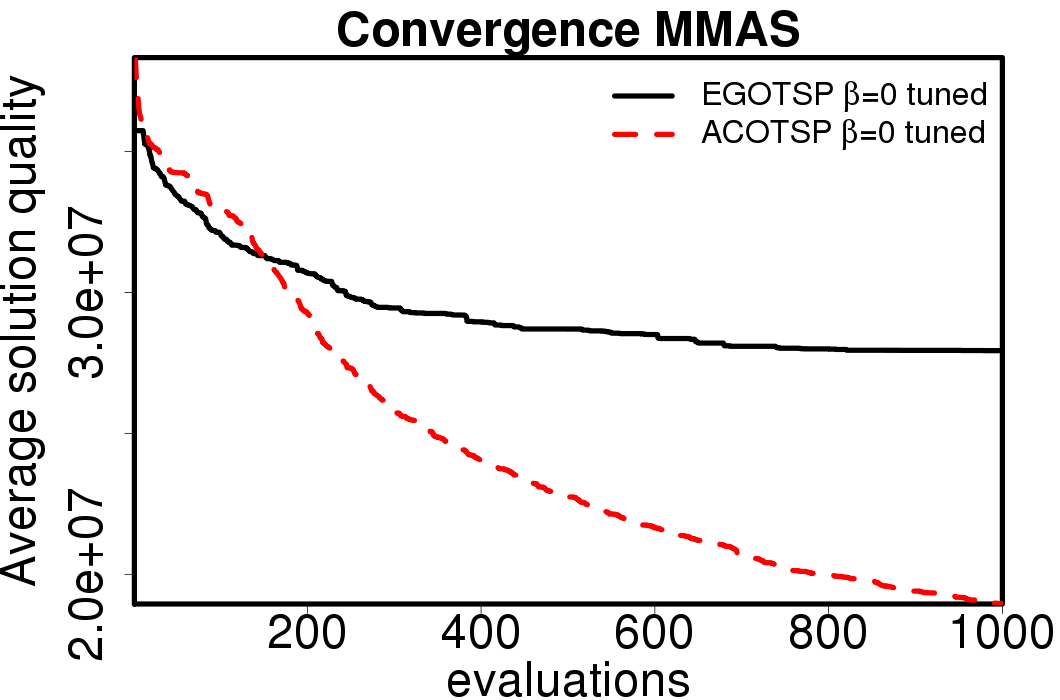 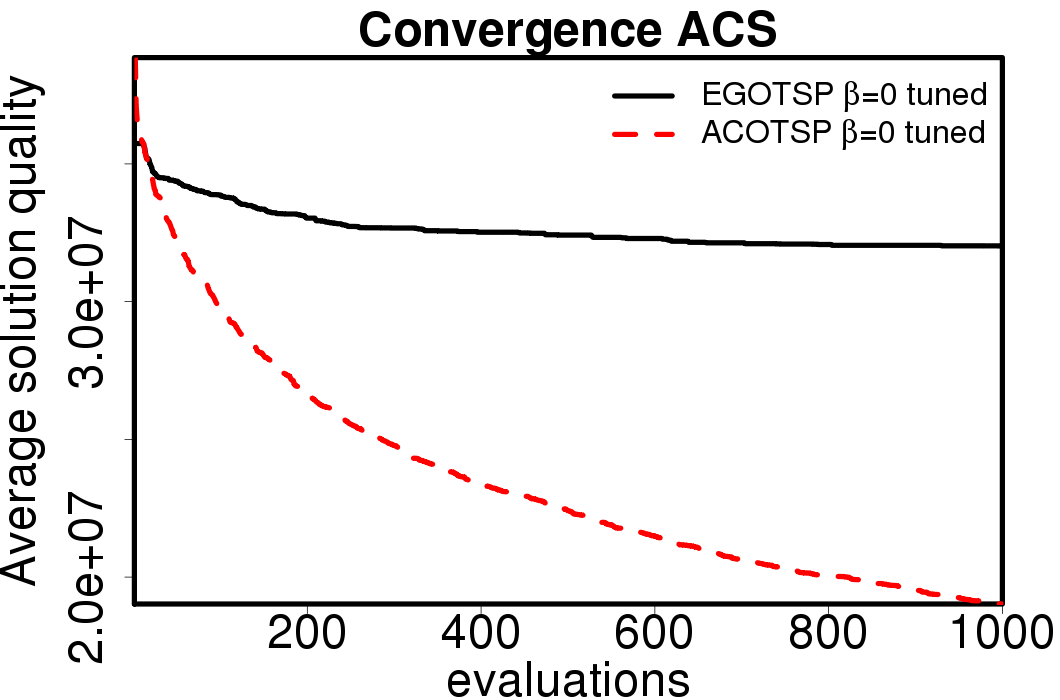
|
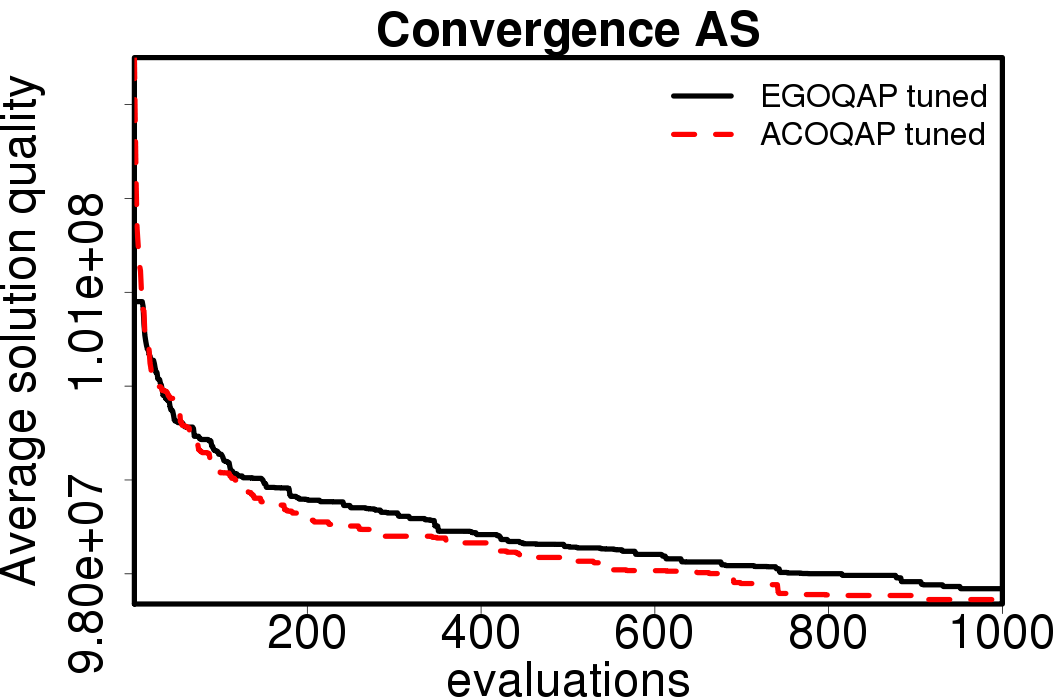 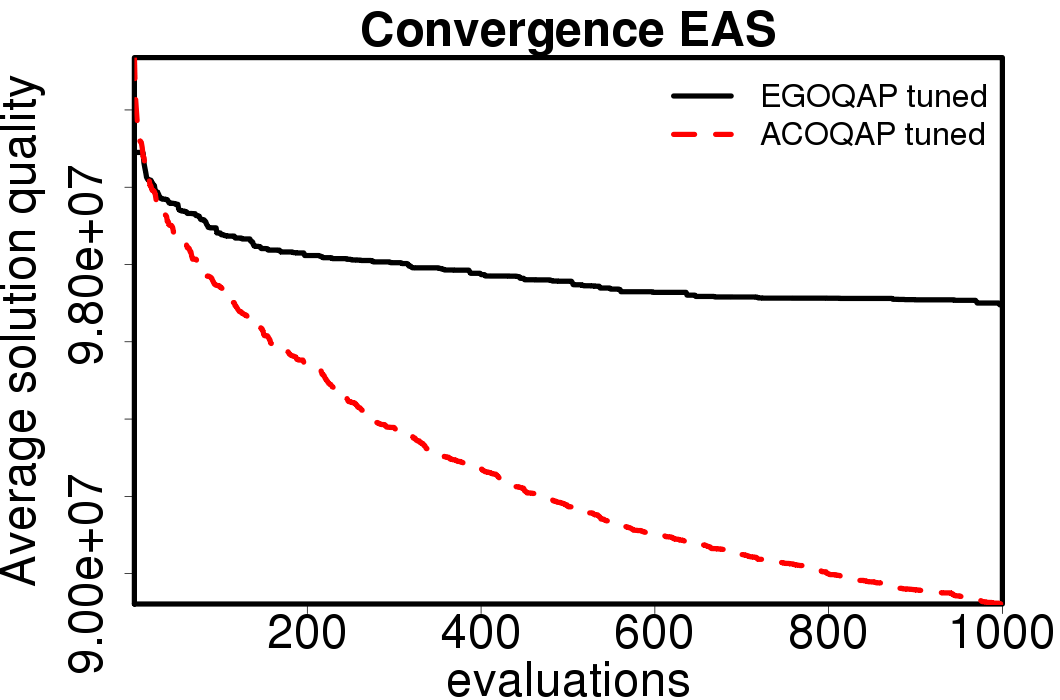 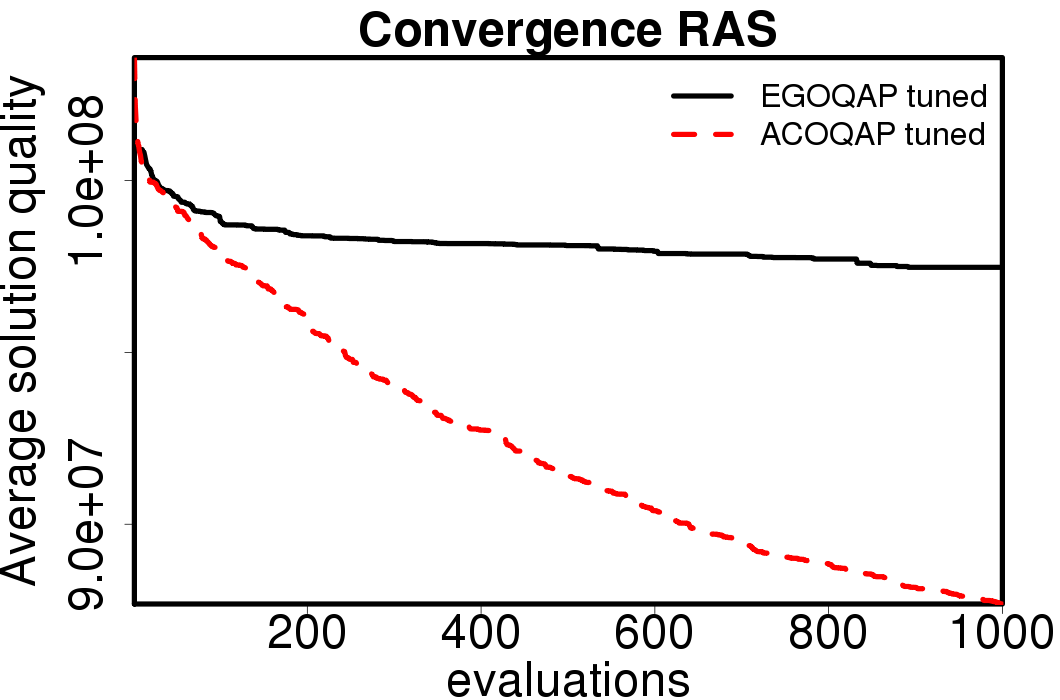  
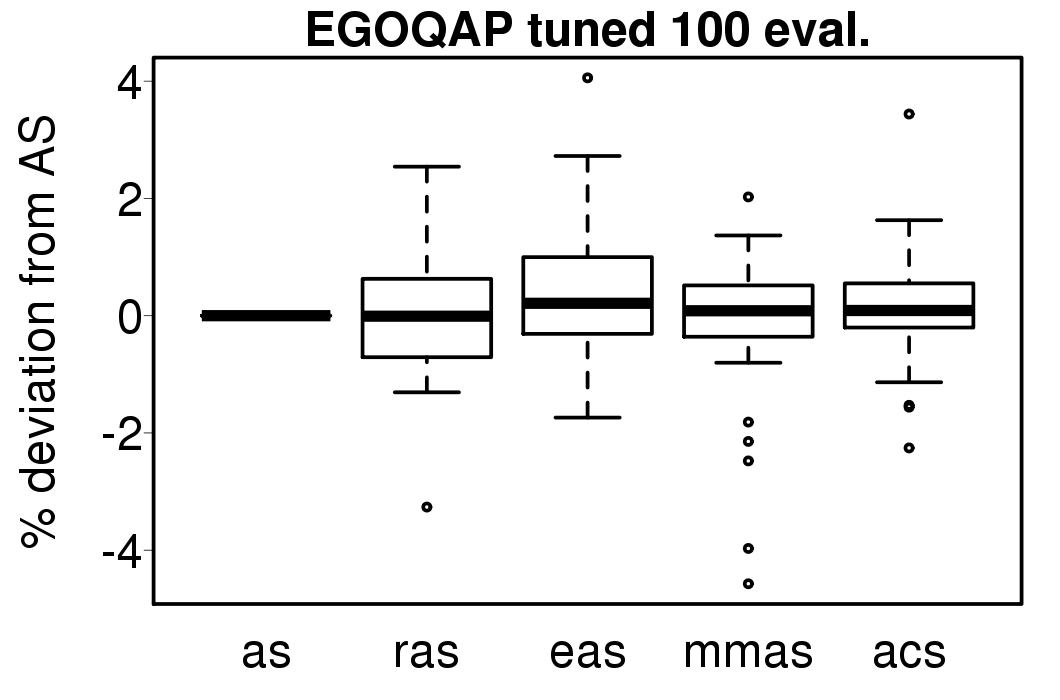
|
We perform the tuning of the ACO parameters defined in Table 2 inside the EGO algorithms following the tune-EGOTSP and tune-EGOQAP scenarios and also directly on the ACO algorithms. The relative percentage deviation from EGO-AS / AS of the EGO-ACO / ACO algorithms is shown in the following plots:
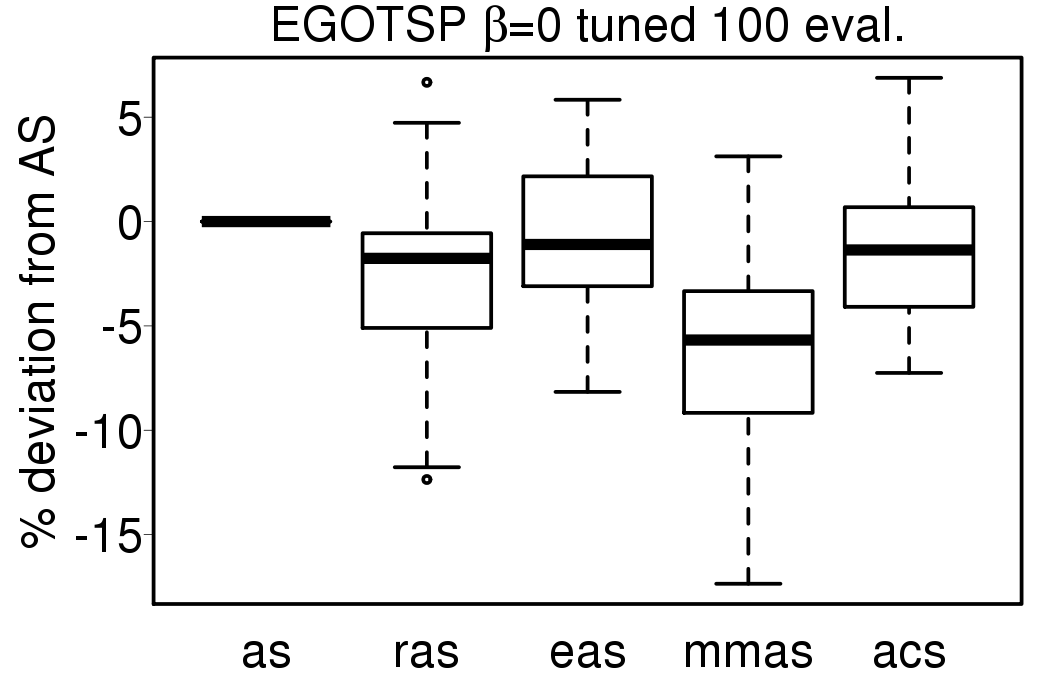
|
 |
The following plots compare the obtained results with the EGO-ACO algorithms tuned for 100 evaluations using default parameters and with the tuned version of the ACO algorithms tuned for 100 evaluations.
|
 |
|
 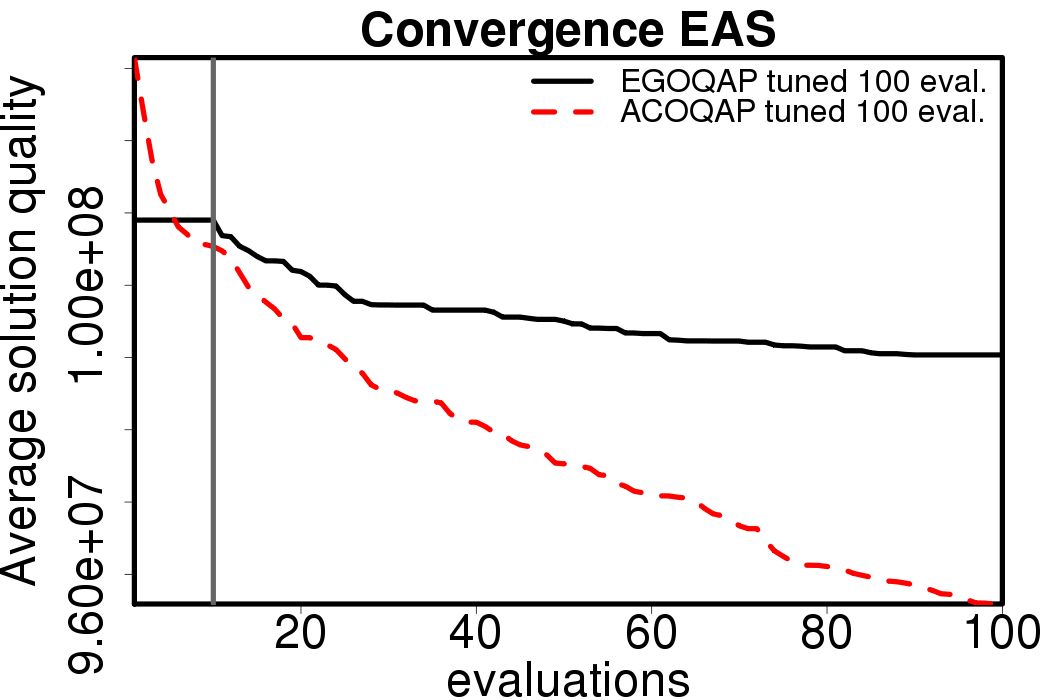 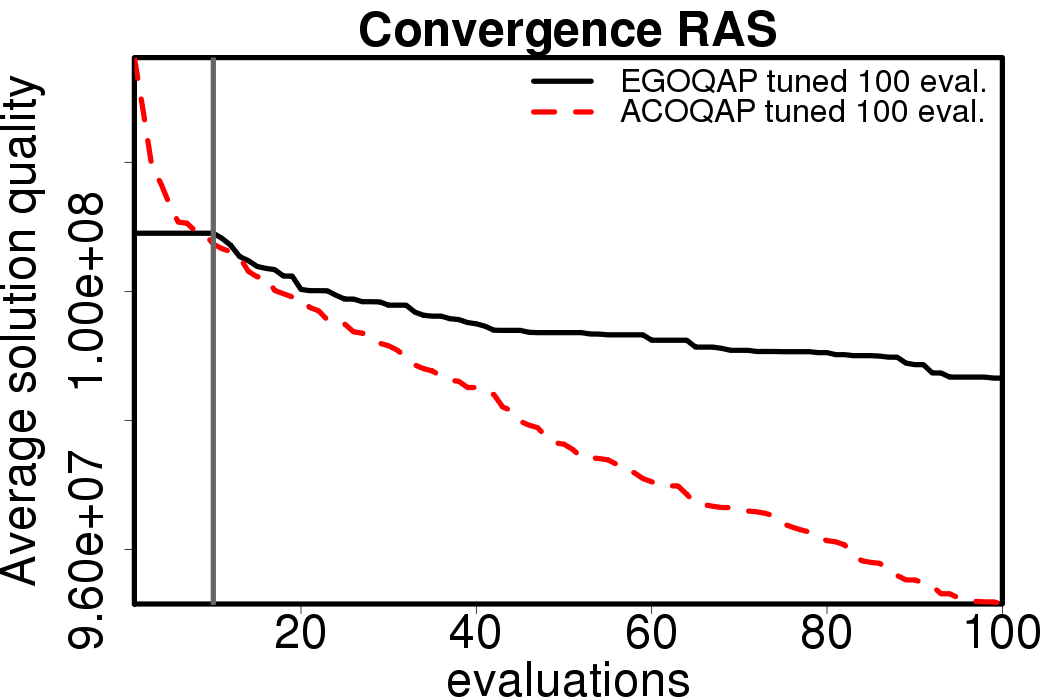 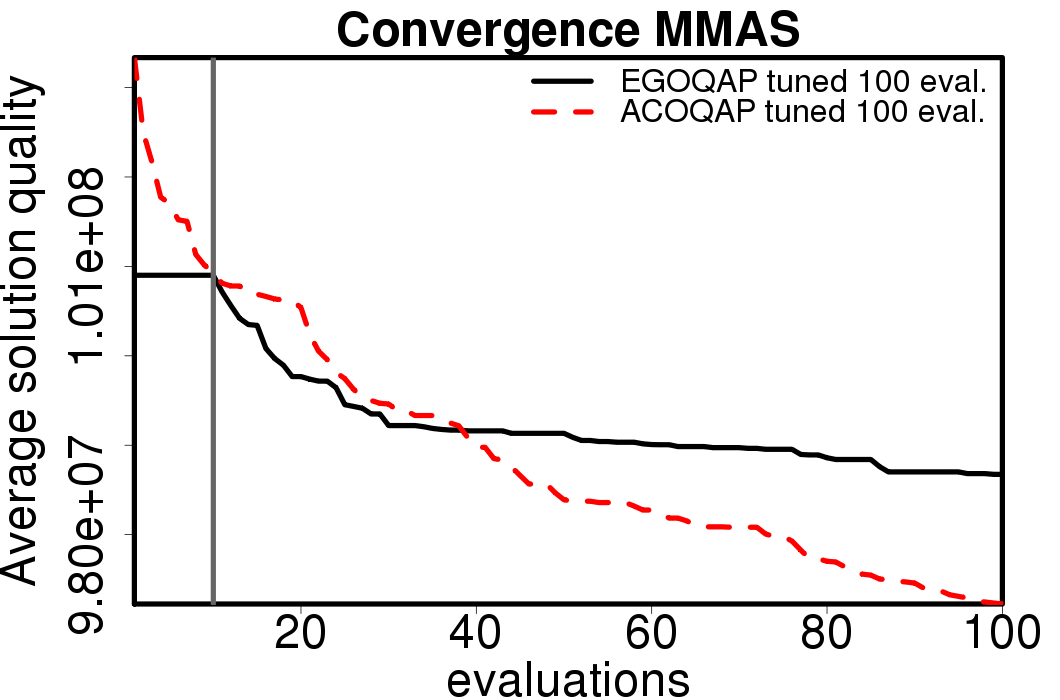 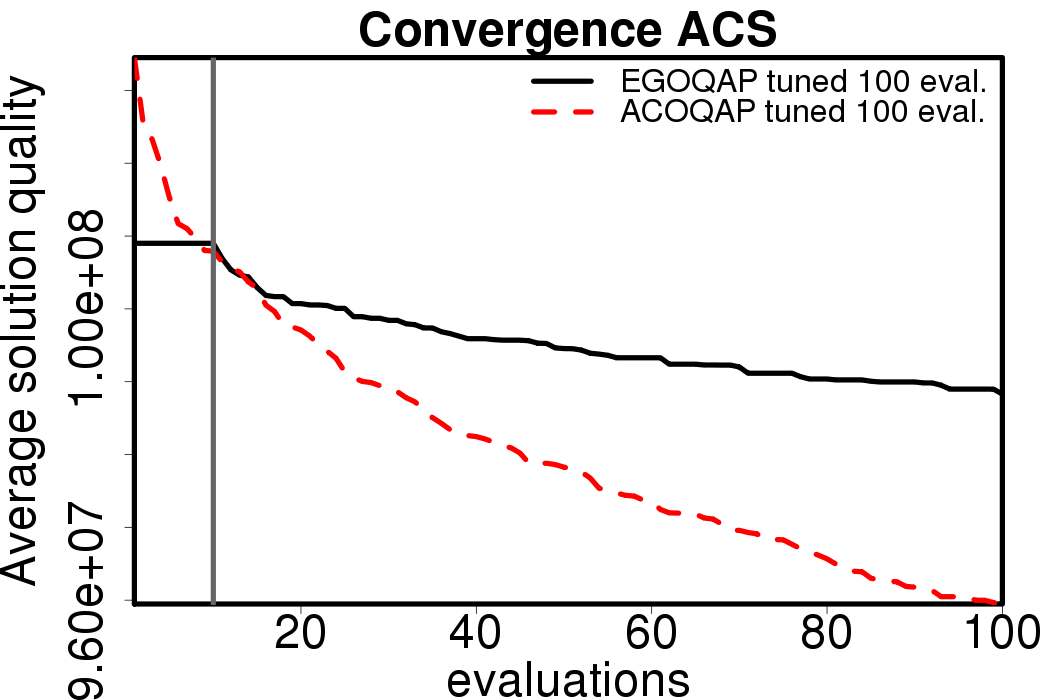
|
We execute the experiments allowing the use of heuristic information for the TSP. The following plots show the results of the ACO algorithms using default settings and tuned settings.
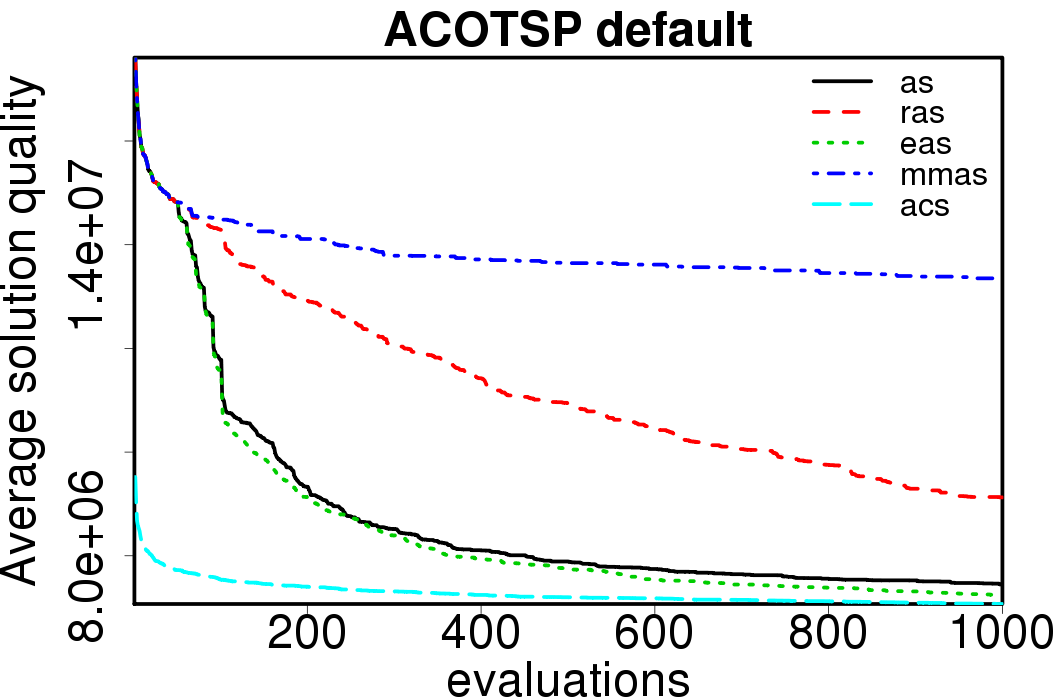
|
|
The tuned parameter settings used are the ones described in Table 4
.| algorithm | ants | alpha | beta | rho | q0 | rasrank | elitistants |
|---|---|---|---|---|---|---|---|
| AS | 69 | 1.84 | 3.59 | 0.18 | 0.11 | − | − |
| EAS | 37 | 0.52 | 5.67 | 0.74 | 0.04 | − | 542 |
| RAS | 59 | 0.85 | 6.46 | 0.53 | 0.25 | 5 | − |
| MMAS | 18 | 0.59 | 6.19 | 0.91 | 0.48 | − | − |
| ACS | 57 | 5.24 | 9.72 | 0.65 | 0.1 | − | − |
The following plots show the deviation of the results of the ACO algorithms using default settings and the algorithms using tuned settings.
|
In this case not all the algorithms strongly improve their results like in the case without heuristic information.
|
We execute the EGO algorithms using default and tuned settings, the following plots compare the EGO-ACO algorithms with EGO-AS.
|
|
The following plots compare the EGO-ACO and the ACO algorithms.
|
|
|
|
The implementation of the ACO algorithms we use have the option of using the parameter q0 for all the algorithms. The following plots compare the performance of the ACO algorithms tuned without heuristic information and without using q0.
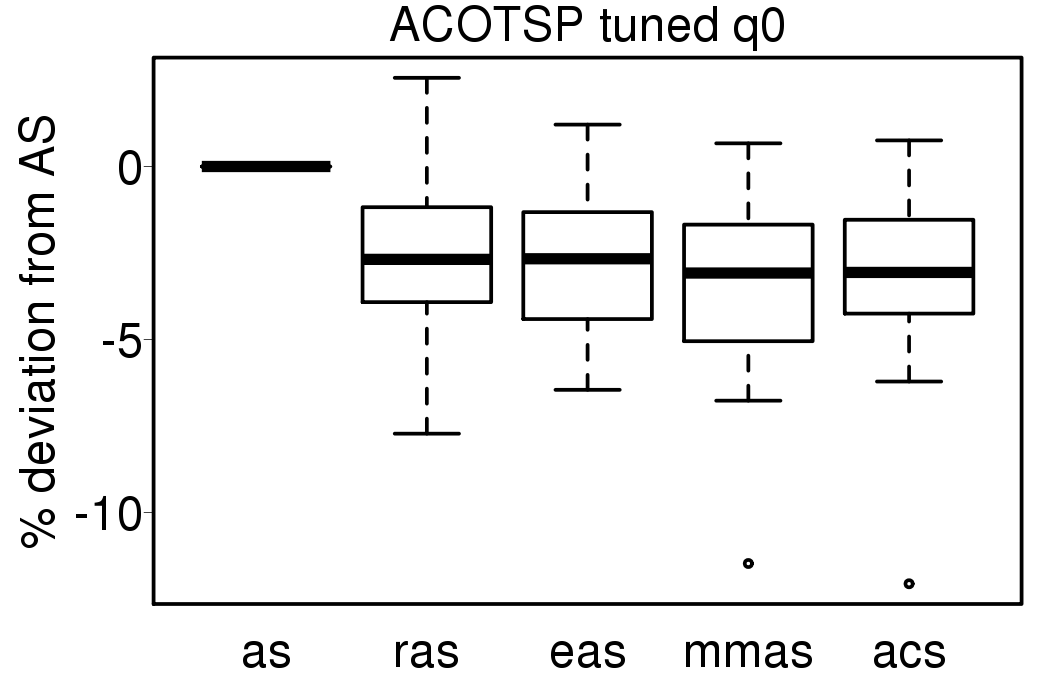
|
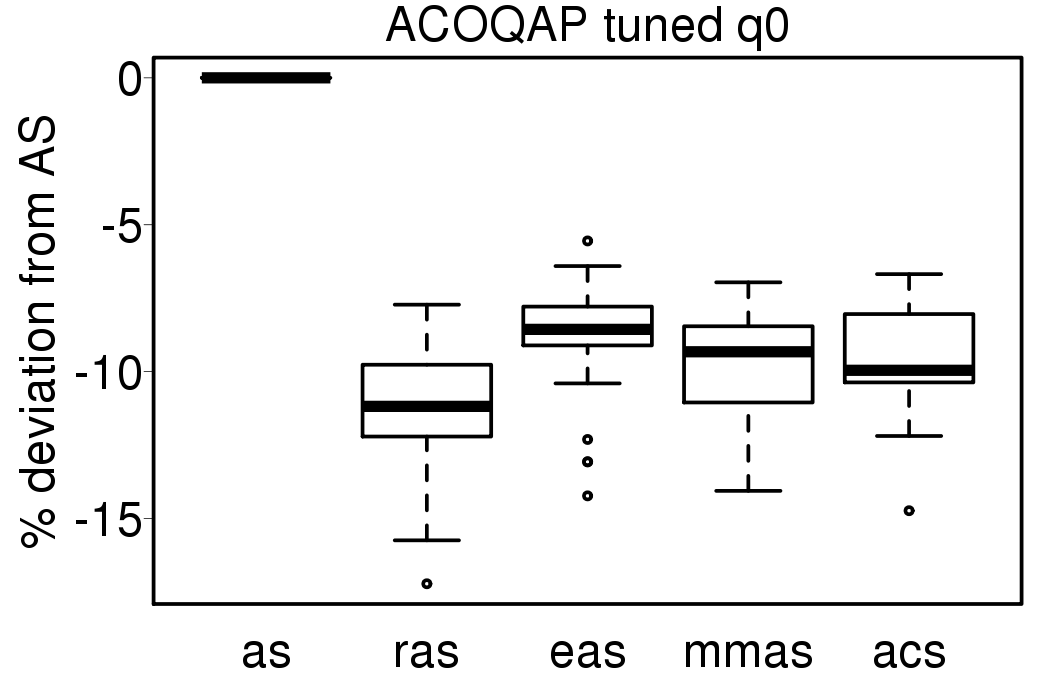
|
The relative results are not very different from the obtained by the versions of the ACO algorithms tuned using the q0 parameter.
We perform the tuning over the basic ACOTSP and ACOQAP algorithms, without heuristic information. We repeat the tuning 20 times to analyse the distribution of values of the parameters.
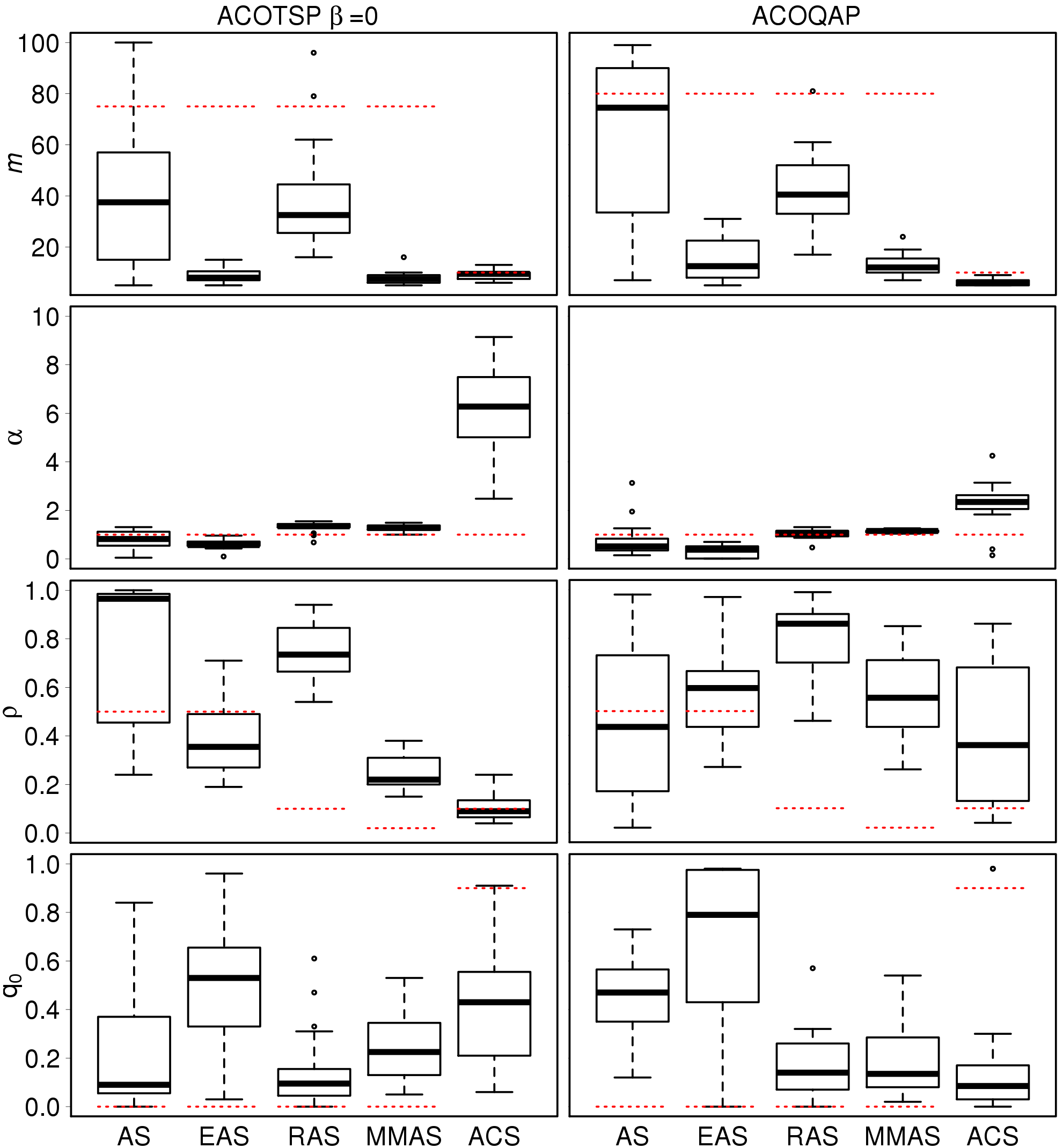 |
The following plots show the parameters tuned 20 times, this time using heuristic information.
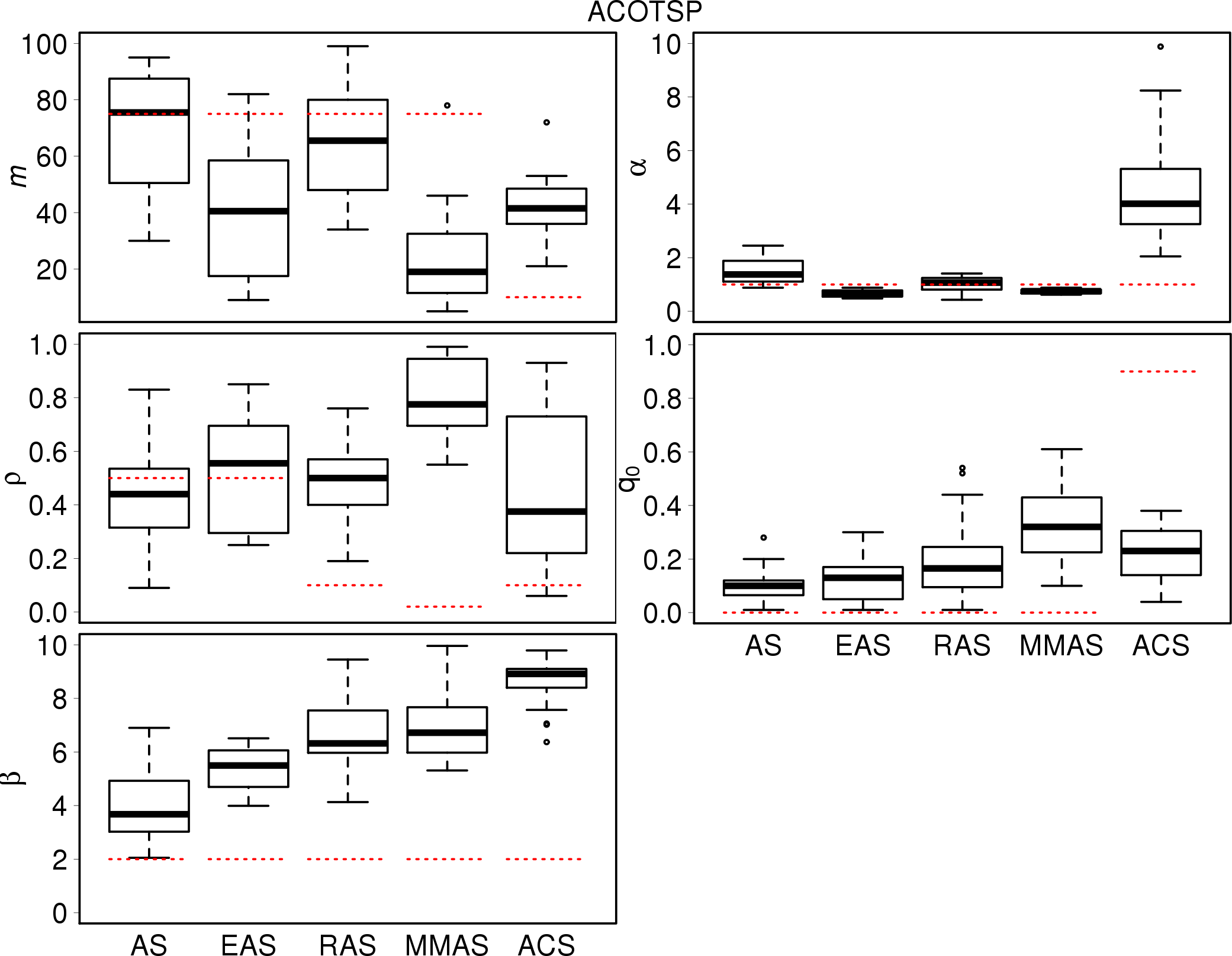 |
We perform the same tuning process for the ACO algorithms restricted to 100 evaluations only.
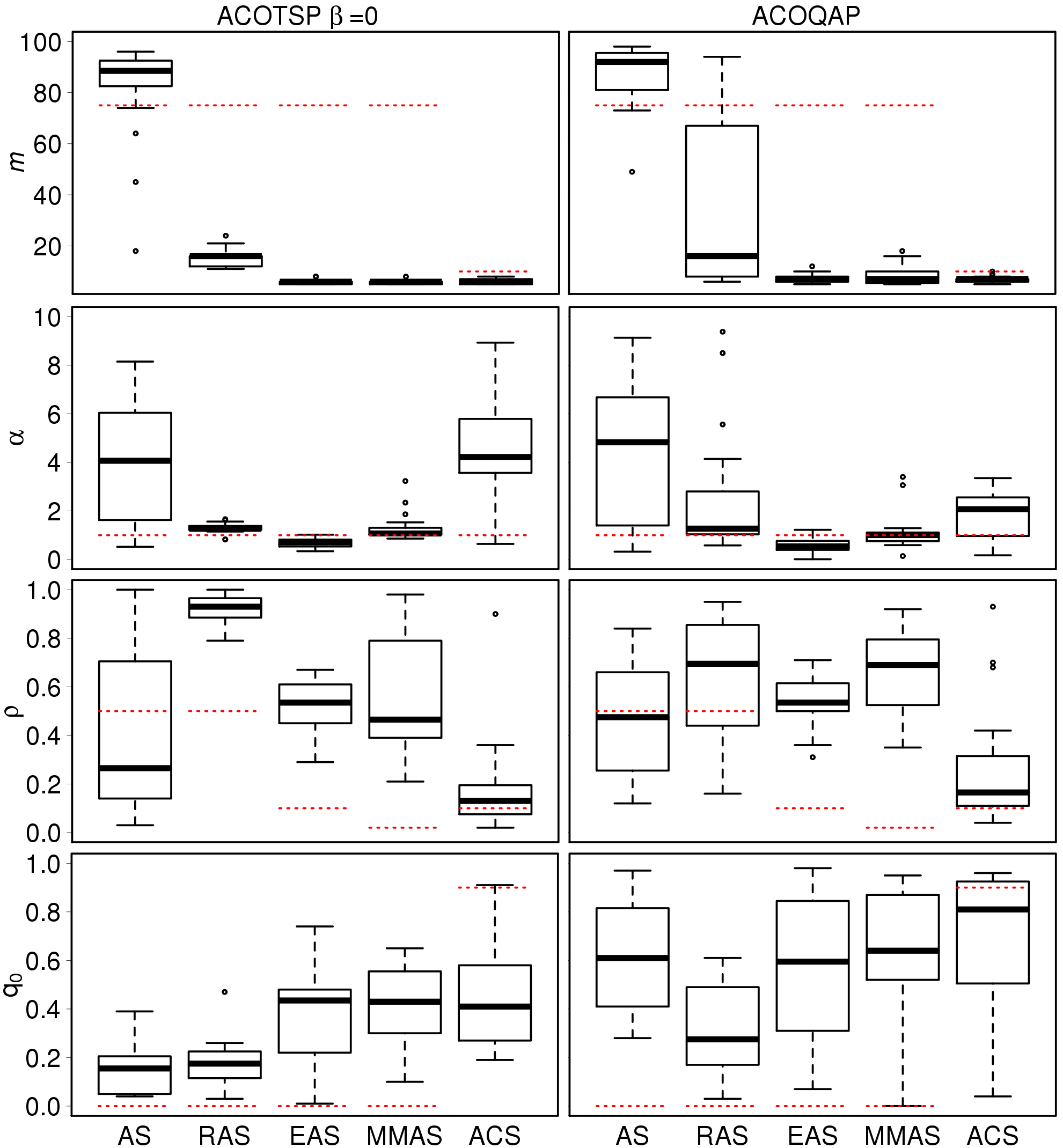 |
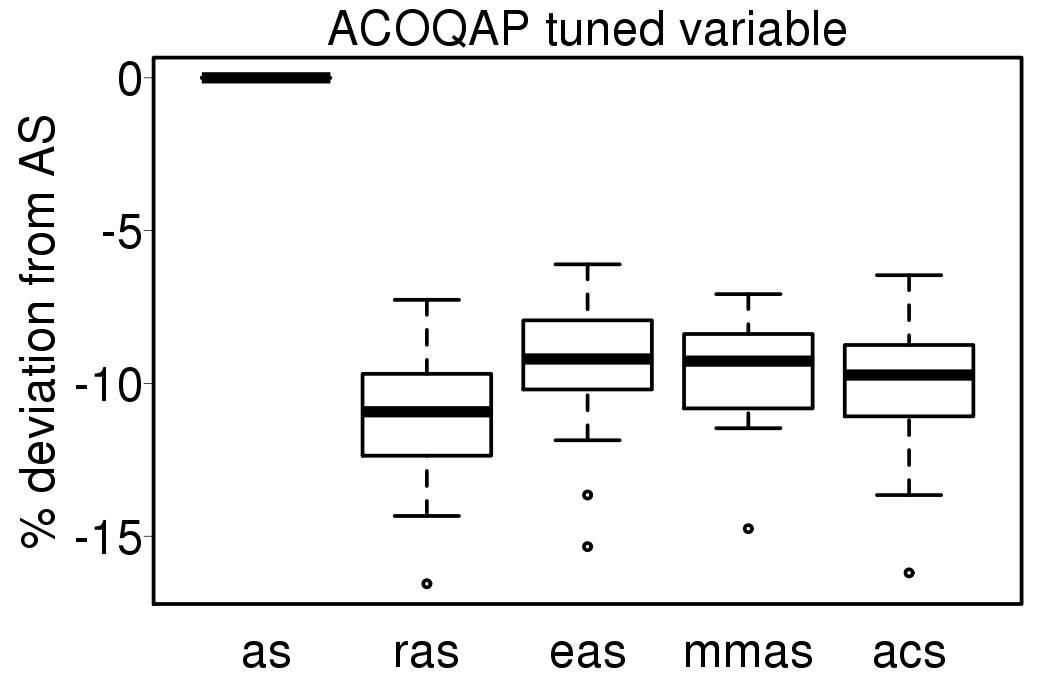
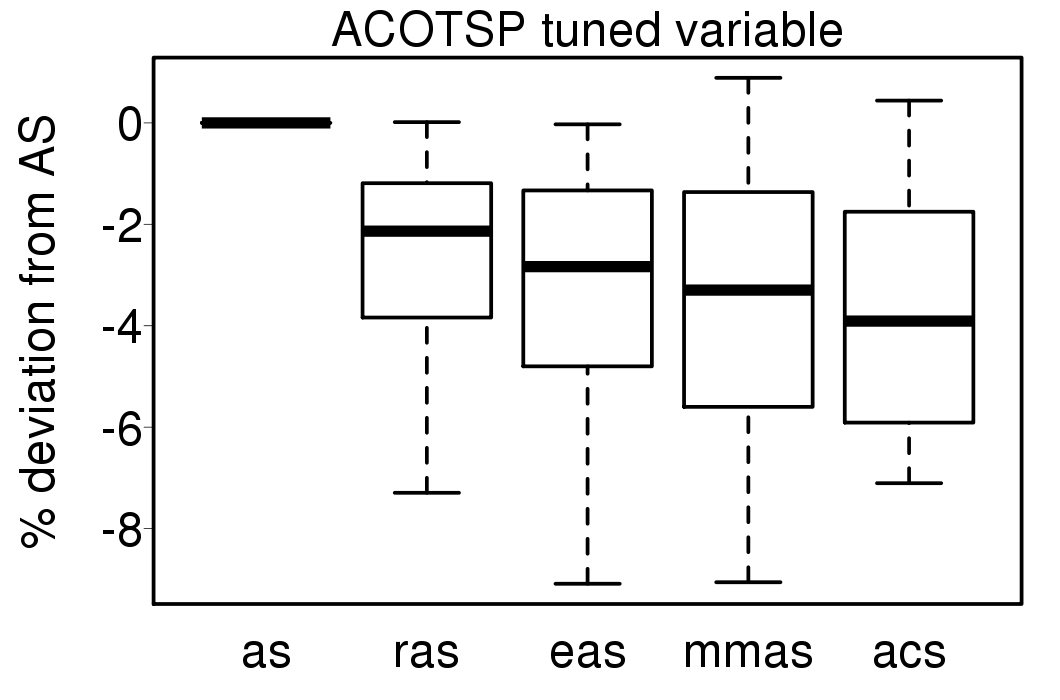
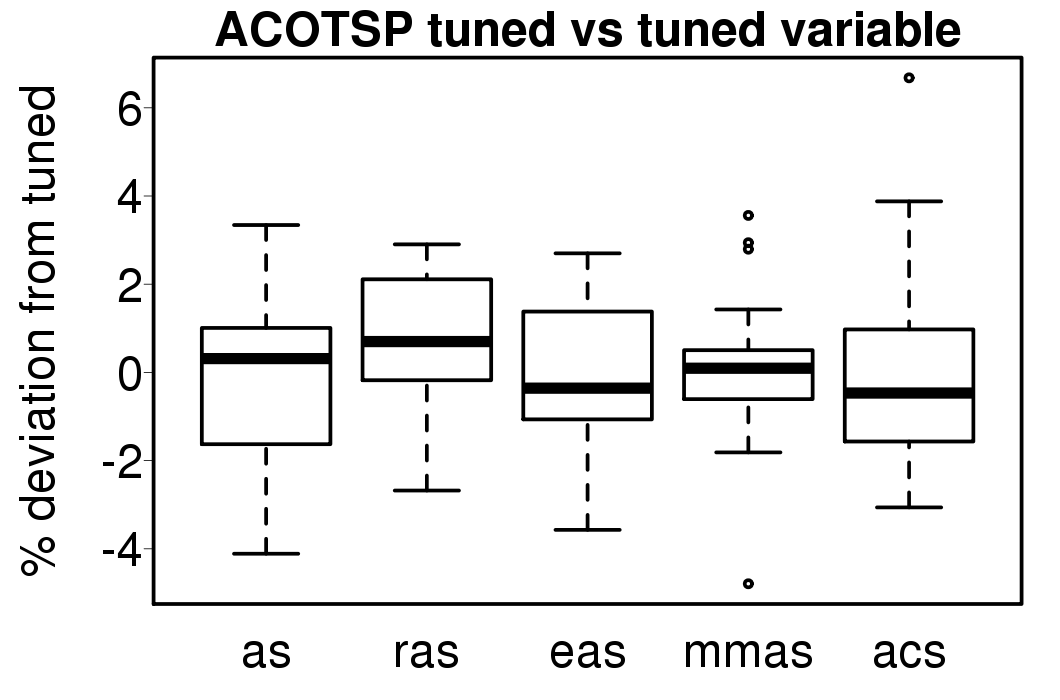
Finally, we executed the ACO algorithms using a variable parameter scheme used in the first work we presented in [7], the description can be found in [5]. The following plots show the relative percentage deviation of the results of the ACO variable algorithms from the results obtained by the variable AS.
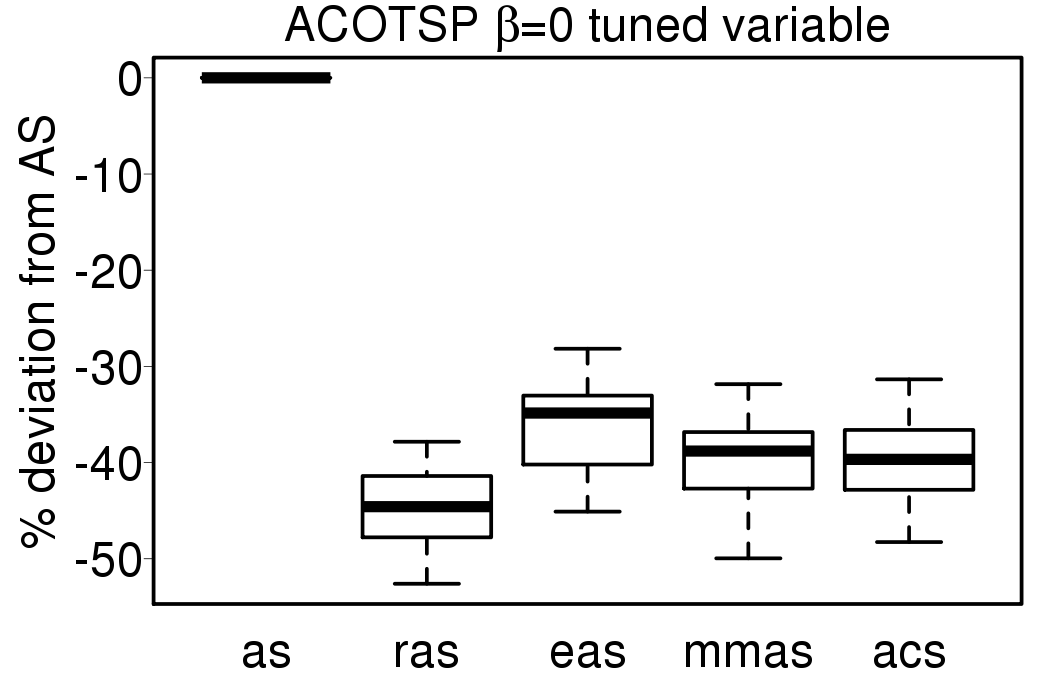
|
|
|
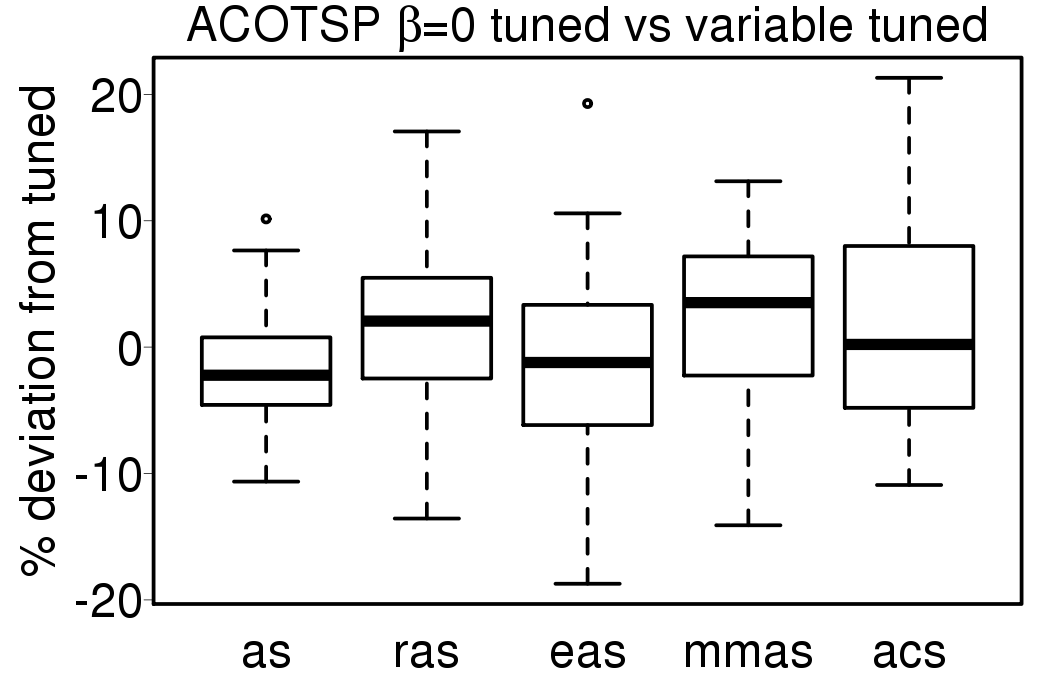
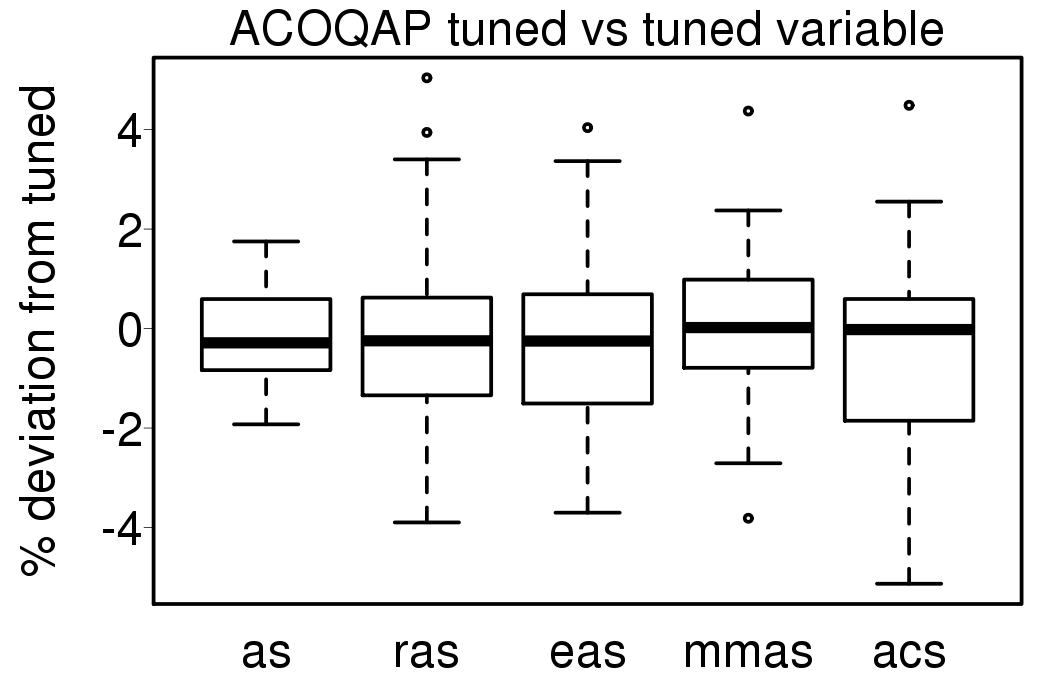
Comparing the results with the tuned version of each ACO algorithm without variation of parameters:
|
|
|
[1] Dorigo, M., Maniezzo, V., Colorni, A.: Ant System: Optimization by a colony of cooperating agents. IEEE Transactions on Systems, Man, and Cybernetics − Part B 26(1), 29−41 (1996)
[2] Bullnheimer, B., Hartl, R., Strauss, C.: A new rank-based version of the Ant System: A computational study. Central European Journal for Operations Research and Economics 7(1), 25−38 (1999)
[3] Stützle, T., Hoos, H.H.: MAX−MIN Ant System. Future Generation Compute Systems 16(8), 889−914 (2000)
[4] Dorigo, M., Gambardella, L.M.: Ant Colony System: A cooperative learning approach to the traveling salesman problem. IEEE Transactions on Evolutionary Computation 1(1), 53−66 (1997)
[5] López−Ibánez, M., Stützle, T.: Automatically improving the anytime behaviour of optimisation algorithms. European Journal of Operational Research 235(3), 569−582 (2014)
[6] Pellegrini, P., Mascia, F., Stützle, T., Birattari, M.: On the sensitivity of reactive tabu search to its meta-parameters. Soft Computing (In press)
[7] Pérez Cáceres, L., López−Ibánez, M., Stützle, T.: Ant colony optimization on a budget of 1000. 8th International conference on Swarm Intelligence (ANTS2014). LNCS vol. 8667, pages 50−61, Springer (2014)
[8] Zaefferer M., Stork, J., Friese, M., Fischbach A., Naijoks, B., Batrz-Beielstein T.: Efficient Global optimization for combinatorial problems. Proceedings of the Genetic and Evolutionsry Computation Conference (GECCO2014), pages 871−878, ACM Press (2014)