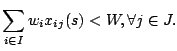Supplementary material for the paper:
On the Invariance of Ant Colony Optimization
Mauro Birattari, Paola Pellegrini, and Marco Dorigo
mbiro@ulb.ac.be; paolap@pellegrini.it; mdorigo@ulb.ac.be
The following information is extracted from: P. Pellegrini and M. Birattari (2006)
Some combinatorial optimization problems on which ant colony
optimization is invariant. Technical Report TR/IRIDIA/2006-026,
IRIDIA, Université Libre de Bruxelles, Brussels, Belgium.
The traveling salesman problem
(TSP) consists in finding a Hamiltonian circuit of minimum cost on
an edge-weighted graph 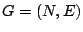 . Let
. Let 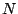 be the set of nodes, and
be the set of nodes, and
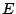 be the set of edges. If a directed graph is considered, the
problem is known as the asymmetric traveling salesman
problem (1).
be the set of edges. If a directed graph is considered, the
problem is known as the asymmetric traveling salesman
problem (1).
Let 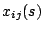 be a binary variable taking value 1 if edge
be a binary variable taking value 1 if edge
 is
included in tour
is
included in tour  , and 0 otherwise. Let
, and 0 otherwise. Let 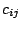 be the cost
associated to edge
be the cost
associated to edge
 . The goal is to find a
tour
. The goal is to find a
tour  such that the function
such that the function
is minimized.
- Transformation of units:
- If the
cost of all edges is multiplied by a constant
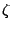 , the resulting
instance
, the resulting
instance 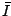 is equivalent to the original
is equivalent to the original 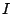 , that is,
, that is,
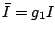 , with
, with 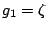 .
Indeed,
.
Indeed,
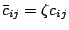 , for all
, for all

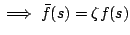 , for all
, for all  .
.
- Reference solution:
- Many constructive
heuristics exist for the TSP (2) that
can be conveniently adopted here.
- Heuristic information:
- The typical
setting is
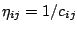 , for all
, for all
 . This meets
Condition 1 with
. This meets
Condition 1 with
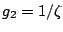 .
.
Therefore, the theorems on the weak invariance of ant system,
 -
-
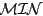 ant system, and ant colony system
hold. In the literature, the three variants of ant colony optimization
considered in this paper have been applied to the traveling salesman
problem with the setup just described (3).
ant system, and ant colony system
hold. In the literature, the three variants of ant colony optimization
considered in this paper have been applied to the traveling salesman
problem with the setup just described (3).
- Strongly-invariant heuristic
information:
- Let
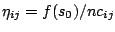 , for all
, for all
 ,
where
,
where 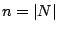 . It is worth noting that the term
. It is worth noting that the term 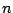 is not needed
for the invariance to transformation of units. It has been included
for achieving another property: the above defined
is not needed
for the invariance to transformation of units. It has been included
for achieving another property: the above defined 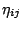 does not
depend on the size of the instance under analysis--that is, on the
number
does not
depend on the size of the instance under analysis--that is, on the
number 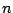 of cities. This definition meets
Condition 2 with
of cities. This definition meets
Condition 2 with
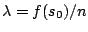 , and
Condition 3.
, and
Condition 3.
Therefore, si AS , si
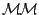 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
In the vehicle routing problem (VRP) 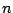 customers have to be served
starting from one central depot (which is indexed 0). Each customer
customers have to be served
starting from one central depot (which is indexed 0). Each customer
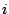 has a non-negative demand
has a non-negative demand 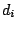 of the same good, and for each
pair of customers
of the same good, and for each
pair of customers
 a travel time
a travel time 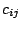 between the two
customers is given. The customers are served by a fleet of vehicles
of equal capacity. The objective is to find a set of routes that
minimizes the total travel time, such that: each customer is served
once by exactly one vehicle; the route of each vehicle starts and
ends at the depot; and the total demand covered by each vehicle does
not exceed its capacity. Using the notation introduced for the
traveling salesman problem, the objective function can be written
as:
between the two
customers is given. The customers are served by a fleet of vehicles
of equal capacity. The objective is to find a set of routes that
minimizes the total travel time, such that: each customer is served
once by exactly one vehicle; the route of each vehicle starts and
ends at the depot; and the total demand covered by each vehicle does
not exceed its capacity. Using the notation introduced for the
traveling salesman problem, the objective function can be written
as:
Variants of the problem may have different goals, as for example the
minimization of the number of vehicles used (4).
- Transformation of units:
- If the
cost of all edges is multiplied by a constant
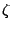 , the resulting
instance
, the resulting
instance 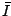 is equivalent to the original
is equivalent to the original 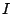 , that is,
, that is,
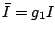 , with
, with 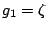 .
Indeed,
.
Indeed,
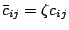 , for all
, for all

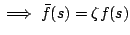 , for all
, for all  .
.
- Reference solution:
- Many constructive
heuristics exist for the VRP (4) that
can be conveniently adopted here.
- Heuristic information:
- Let
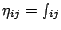 (5), with
(5), with
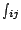 measure of the cost saving that would be
achievable by using edge
measure of the cost saving that would be
achievable by using edge
 (6): We
first consider a solution with one separate tour per customer,
i.e. tours starting and ending at the depot and touching only one
customer each. Then, for each pair
(6): We
first consider a solution with one separate tour per customer,
i.e. tours starting and ending at the depot and touching only one
customer each. Then, for each pair
 of customers, a saving
of customers, a saving
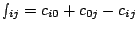 is computed. This meets
Condition 1 with
is computed. This meets
Condition 1 with 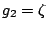 .
.
Therefore, the theorems on the weak invariance of ant system,
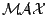 -
-
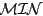 ant system, and
ant colony system hold. In the literature, variants of the VRP have been tacked
with ACO algorithm. Limiting this survey to the standard version,
let us cite, among the others, Bullnheimer et al. (5); Reimann et al. (7).
ant system, and
ant colony system hold. In the literature, variants of the VRP have been tacked
with ACO algorithm. Limiting this survey to the standard version,
let us cite, among the others, Bullnheimer et al. (5); Reimann et al. (7).
- Strongly-invariant heuristic
information:
- Let
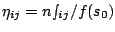 , for all
, for all
 ,
where
,
where 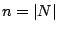 . As in the case of the traveling salesman problem,
the term
. As in the case of the traveling salesman problem,
the term 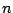 is not needed
for the invariance to transformation of units. It has been included
for achieving another property: the above defined
is not needed
for the invariance to transformation of units. It has been included
for achieving another property: the above defined 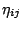 does not
depend on the size of the instance under analysis--that is, on the
number
does not
depend on the size of the instance under analysis--that is, on the
number 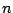 of cities. This definition meets
Condition 2 with
of cities. This definition meets
Condition 2 with
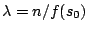 , and
Condition 3.
, and
Condition 3.
Therefore, si AS , si
 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
The sequential ordering problem (SOP) consists in finding a minimum
weight hamiltonian path on a directed graph with weights on edges
and nodes, subject to precedence constraints (8). It is
often tackled as a constrained version of the asymmetric traveling
salesman problem, by associating to each edge
 a cost
a cost
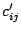 :
:
where 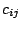 is the weight of edge
is the weight of edge
 , and
, and 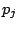 is the
weight of node
is the
weight of node  . With this feature the objective function can be
expressed as
. With this feature the objective function can be
expressed as
using the notation introduced for the TSP.
- Transformation of units:
- If the
cost of both edges and nodes is multiplied by a constant
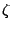 ,
then the cost
,
then the cost
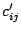 is scaled by the same constant
is scaled by the same constant
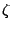 , for all
, for all
 . The resulting instance
. The resulting instance 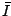 is equivalent to the original
is equivalent to the original 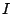 , that is,
, that is,
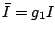 ,
with
,
with 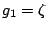 .
Indeed,
.
Indeed,
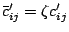 , for all
, for all

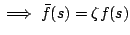 , for all
, for all  .
.
- Reference solution:
- For the construction
of a reference solution, one of the heuristics available for the TSP
(2) can be conveniently adopted.
- Heuristic information:
- The typical
setting is
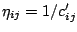 , for all
, for all
 . This meets
Condition 1 with
. This meets
Condition 1 with
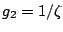 .
.
Therefore, the theorems on the weak invariance of ant system,
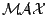 -
-
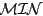 ant system, and
ant colony system hold. One of the best algorithms available in the literature
for the sequential ordering problem is the hybrid ant colony system
proposed by Gambardella and Dorigo (9), where the authors use this
invariant setup.
ant system, and
ant colony system hold. One of the best algorithms available in the literature
for the sequential ordering problem is the hybrid ant colony system
proposed by Gambardella and Dorigo (9), where the authors use this
invariant setup.
- Strongly-invariant heuristic
information:
- Let
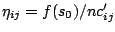 , for all
, for all
 ,
where
,
where 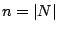 . This definition meets
Condition 2 with
. This definition meets
Condition 2 with
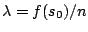 , and
Condition 3.
, and
Condition 3.
Therefore, si AS , si
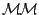 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
In the quadratic assignment problem (QAP), 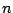 facilities and
facilities and 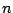 locations are given, together with two
locations are given, together with two 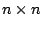 matrices
matrices
![$ A=[a_{uv}]$](img45.png) and
and
![$ B=[b_{ij}]$](img46.png) , where
, where 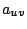 is the distance
between locations
is the distance
between locations 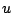 and
and 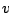 , and
, and 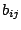 is the flow
between facilities
is the flow
between facilities 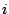 and
and  .
A solution
.
A solution  is an assignment of each facility to a location. Let
is an assignment of each facility to a location. Let
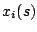 denote the location to which facility
denote the location to which facility 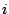 is assigned.
The goal is to find an assignment that minimizes the function:
is assigned.
The goal is to find an assignment that minimizes the function:
- Transformation of units:
- If all
distance are multiplied by a constant
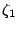 and all flows by a
constant
and all flows by a
constant 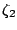 , the resulting instance
, the resulting instance 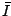 is equivalent to the
original
is equivalent to the
original 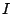 , that is,
, that is,
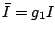 , with
, with
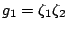 .
.
- Reference solution:
- The construction of
the reference solution is typically stochastic: a number of
solutions are randomly generated and improved through a local
search. The best solution obtained is adopted as the reference
solution (10). It is worth noting that a local
search is an invariant algorithm.
- Heuristic information:
- Often, the
heuristic information is not adopted (10),
that is,
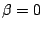 . In this case,
Condition 1 is trivially met. Some
authors (11,12) set
. In this case,
Condition 1 is trivially met. Some
authors (11,12) set
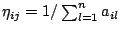 . This meets
Condition 1 with
. This meets
Condition 1 with
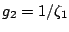 .
.
Therefore, the theorems on the weak invariance of ant system,
 -
-
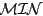 ant system, and ant colony system
hold.
ant system, and ant colony system
hold.
- Strongly-invariant heuristic
information:
- If the heuristic information is adopted,
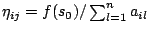 , for all
, for all
 . This
meets Condition 2 with
. This
meets Condition 2 with
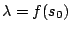 , and
Condition 3.
On the other hand, if no heuristic information is adopted as
suggested in (10),
Conditions 2
and 3 are trivially met.
, and
Condition 3.
On the other hand, if no heuristic information is adopted as
suggested in (10),
Conditions 2
and 3 are trivially met.
Therefore, si AS , si
 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
In the generalized assignment problem (GAP), a set of tasks 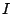 has
to be assigned to a set of agents
has
to be assigned to a set of agents 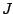 in such a way that a cost
function is minimized. Each agent
in such a way that a cost
function is minimized. Each agent  has only a limited capacity
has only a limited capacity
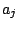 , and each task
, and each task 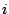 consumes, when assigned to agent
consumes, when assigned to agent  , a
quantity
, a
quantity 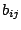 of the agent's capacity. Moreover, a cost
of the agent's capacity. Moreover, a cost 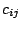 of assigning task
of assigning task 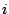 to agent
to agent  is given. The objective is to
find a feasible task assignment
is given. The objective is to
find a feasible task assignment  that minimizes
that minimizes
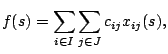 with with 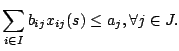 |
|
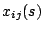 is equal to 1 if task
is equal to 1 if task 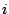 is assigned to agent
is assigned to agent  in
in
 , and 0 otherwise.
, and 0 otherwise.
- Transformation of units:
- If the
cost of assigning each task
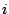 to each agent
to each agent  is multiplied by a constant
is multiplied by a constant 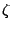 , the resulting
instance
, the resulting
instance 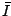 is equivalent to the original
is equivalent to the original 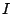 , that is,
, that is,
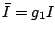 , with
, with 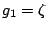 .
.
- Reference solution:
- The construction of
the reference solution is typically stochastic.
- Heuristic information:
- The typical
setting is
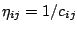 , for all
, for all
 (13).
This meets Condition 1 with
(13).
This meets Condition 1 with
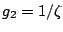 .
.
Therefore, the theorems on the weak invariance of ant system,
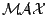 -
-
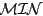 ant system, and
ant colony system hold.
ant system, and
ant colony system hold.
- Strongly-invariant heuristic
information:
- Let
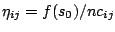 , for all
, for all
 ,
where
,
where 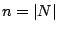 . This definition meets
Condition 2 with
. This definition meets
Condition 2 with
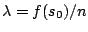 , and
Condition 3.
, and
Condition 3.
Therefore, si AS , si
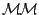 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
In the single machine total weighted tardiness scheduling problem
(SMTWTP) (14), 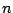 jobs are to be processed
sequentially on a single machine, without interruption. Each job
jobs are to be processed
sequentially on a single machine, without interruption. Each job  has an associated processing time
has an associated processing time 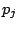 , a weight
, a weight 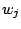 , and a due
date
, and a due
date 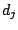 . All jobs are available for processing at time zero. The
tardiness of job
. All jobs are available for processing at time zero. The
tardiness of job  is defined as
is defined as
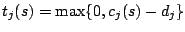 , where
, where 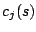 is its completion time in the current job
sequence
is its completion time in the current job
sequence  . The objective is to find the sequence
. The objective is to find the sequence  that
minimizes the sum of the weighted tardiness:
that
minimizes the sum of the weighted tardiness:
- Transformation of units:
- If,
for all the jobs, both the processing time and the due date
are multiplied by a constant
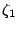 , and the weight
is multiplied by a constant
, and the weight
is multiplied by a constant 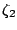 , the resulting
instance
, the resulting
instance 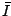 is equivalent to the original
is equivalent to the original 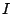 , that is,
, that is,
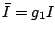 , with
, with
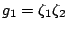 .
.
- Reference solution:
- A heuristic based
on the apparent urgency (15) is typically
used for the construction of the reference solution.
In this approach, jobs are arranged in the descending order
of their apparent urgency priorities:
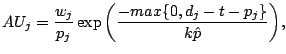 for all for all 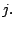 |
|
Here, 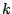 is called the look-ahead parameter and is set according to
the tightness of the due date;
is called the look-ahead parameter and is set according to
the tightness of the due date; 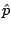 the average processing time;
the average processing time;
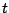 is the current time.
As it can be seen, the selection criterion is invariant to
transformation of units.
is the current time.
As it can be seen, the selection criterion is invariant to
transformation of units.
- Heuristic information:
- The typical
setting is
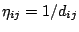 , for all
, for all
 .
This meets Condition 1 with
.
This meets Condition 1 with
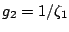 .
.
Therefore, the theorems on the weak invariance of ant system,
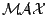 -
-
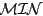 ant system, and
ant colony system hold. In the literature, den Besten et al. (16) apply ant
colony system to SMTWTP. In the analysis, the authors define various
priority rules, which imply various heuristic measures. Among them
the one previously described is considered.
ant system, and
ant colony system hold. In the literature, den Besten et al. (16) apply ant
colony system to SMTWTP. In the analysis, the authors define various
priority rules, which imply various heuristic measures. Among them
the one previously described is considered.
- Strongly-invariant heuristic
information:
- Let
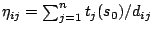 , for all
, for all
 . This definition meets
Condition 2 with
. This definition meets
Condition 2 with
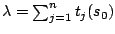 , and Condition 3.
, and Condition 3.
Therefore, si AS , si
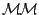 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
In open shop scheduling problems (OSP) (17), a finite
set
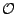 of operations is given, which is partitioned into a
collection of subsets
of operations is given, which is partitioned into a
collection of subsets
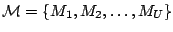 and a
collection of subsets
and a
collection of subsets
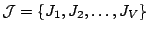 . Each
. Each 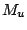 is the set of operations that have to be performed by machine
is the set of operations that have to be performed by machine 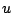 ; and
each
; and
each 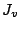 is the set of operations belonging to job
is the set of operations belonging to job 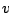 .
A non-negative processing time
.
A non-negative processing time 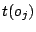 and the earliest
possible starting time
and the earliest
possible starting time 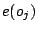 are associated with operation
are associated with operation
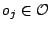 .
A solution
.
A solution  is a collection of schedules
is a collection of schedules
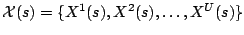 , where
, where 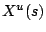 is the sequence of operations scheduled for machine
is the sequence of operations scheduled for machine 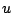 and
and 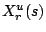 is the operation in position
is the operation in position 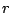 in sequence
in sequence 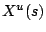 .
The completion time
.
The completion time 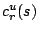 of operation
of operation 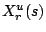 is computed
recursively from
is computed
recursively from
![$ c^u_{r'}(s)=t\big(X^u_{r'}(s)\big)+
\max\big[e\big(X^u_{r'}(s)\big),c^u_{r'-1}(s)\big]$](img90.png) ,
with
,
with
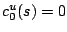 .
The goal is to minimize the makespan, which is given by:
.
The goal is to minimize the makespan, which is given by:
- Transformation of units:
- If all
processing times and earliest possible starting times are multiplied
by a constant
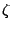 , the resulting instance
, the resulting instance 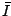 is equivalent to
the original
is equivalent to
the original 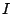 , that is,
, that is,
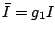 , with
, with 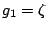 .
.
- Reference solution:
- The construction of
the reference solution is typically stochastic.
- Heuristic information:
- The heuristic
information is
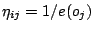 , for all
, for all
 , which meets
Condition 1 with
, which meets
Condition 1 with
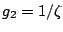 .
.
Therefore, the theorems on the weak invariance of ant system,
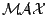 -
-
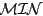 ant system, and ant colony system
hold.
ant system, and ant colony system
hold.
- Strongly-invariant heuristic
information:
- The heuristic information is
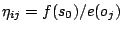 ,
for all
,
for all
 . This meets
Condition 2 with
. This meets
Condition 2 with
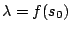 , and
Condition 3.
, and
Condition 3.
Therefore, si AS , si
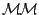 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
In the Permutation flow shop scheduling problem (PFSP), 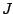 jobs are
to be processed. A set
jobs are
to be processed. A set 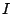 of machines is available. Each job
of machines is available. Each job  is
partitioned in a set of operations
is
partitioned in a set of operations
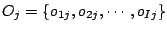 , where operation
, where operation 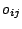 is
to be processed on machine
is
to be processed on machine 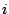 . To each operation
. To each operation 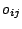 a
processing time
a
processing time 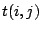 is associated. It may be equal to 0
if job
is associated. It may be equal to 0
if job  is not to be processed on machine
is not to be processed on machine 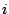 . Let
. Let 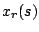 be
the
be
the 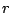 -th job scheduled in sequence
-th job scheduled in sequence  . The completion time
. The completion time
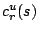 of operation
of operation
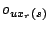 on machine
on machine 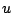 is
computed recursively from
is
computed recursively from
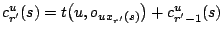 ,
with
,
with
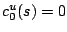 .
.
The goal is to minimize the makespan:
- Transformation of units:
- If
the processing time is multiplied by
a constant
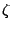 for all the jobs, the resulting
instance
for all the jobs, the resulting
instance 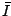 is equivalent to the original
is equivalent to the original 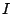 , that is,
, that is,
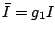 , with
, with 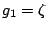 .
.
- Reference solution:
- The NEH heuristic
(15) is typically
used for the construction of the reference solution.
In this approach, first the jobs are ordered by decreasing sums
of total job processing times on the machines. Then, the first
two jobs are scheduled so as to minimize the partial makespan
as if there were only two jobs. Finally, for all the following ones,
insert one job at a time in the partial schedule, into the location
which minimizes the partial makespan.
As it can be seen, the selection criterion is invariant to
transformation of units.
- Heuristic information:
- Typically, the
heuristic information is not adopted (18),
that is,
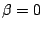 . In this case,
Condition 1 is trivially met.
. In this case,
Condition 1 is trivially met.
Therefore, the theorems on the weak invariance of ant system,
 -
-
 ant system, and
ant colony system hold.
ant system, and
ant colony system hold.
- Strongly-invariant heuristic
information:
- As for the case seen in 3,
if no heuristic information is adopted as
suggested by Stützle (18),
Conditions 2
and 3 are trivially met.
Therefore, si AS , si
 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
In the set covering problem (SCP) (19), 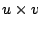 matrix
matrix
![$ A=[a_{ij}]$](img103.png) is given. All the matrix element are either 0 or
1. Additionally, each column is given a non-negative cost
is given. All the matrix element are either 0 or
1. Additionally, each column is given a non-negative cost 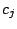 . We
say that a column
. We
say that a column  covers a row
covers a row 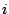 if
if 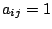 . A solution
. A solution  is represented by a subset of columns that covers every row. Let
is represented by a subset of columns that covers every row. Let
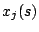 be a binary variable which is 1 if column
be a binary variable which is 1 if column  is included
in
is included
in  , and 0 otherwise. The goal is finding a solution of minimal
cost. The objective function is:
, and 0 otherwise. The goal is finding a solution of minimal
cost. The objective function is:
- Transformation of units:
- If the
cost of all columns is multiplied by a constant
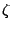 , the resulting
instance
, the resulting
instance 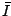 is equivalent to the original
is equivalent to the original 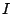 , that is,
, that is,
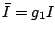 , with
, with 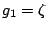 .
.
- Reference solution:
- The construction of
the reference solution is typically stochastic.
- Heuristic information:
- Let
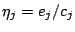 , where
, where 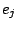 is the cover value
of column
is the cover value
of column  , that is, the number of additional rows covered
when adding column
, that is, the number of additional rows covered
when adding column  to the current partial solution. This meets
Condition 1 with
to the current partial solution. This meets
Condition 1 with
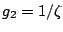 .
.
Therefore, the theorems on the weak invariance of ant system,
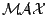 -
-
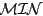 ant system, and
ant colony system hold. Ant system is applied to the set covering problem by
Leguizamón and Michalewicz (20); Hadji et al. (21), using the invariant framework.
ant system, and
ant colony system hold. Ant system is applied to the set covering problem by
Leguizamón and Michalewicz (20); Hadji et al. (21), using the invariant framework.
- Strongly-invariant heuristic
information:
- Let
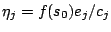 . This meets
Condition 2 with
. This meets
Condition 2 with
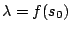 , and
Condition 3.
, and
Condition 3.
Therefore, si AS , si
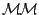 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
The arc-weighted 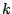 -cardinality tree problem (KCT) is a
generalization of the minimum spanning tree problem. It consists in
finding a subtree with exactly
-cardinality tree problem (KCT) is a
generalization of the minimum spanning tree problem. It consists in
finding a subtree with exactly 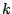 arcs in a graph with arc weights,
such that the sum of the weights is minimal (22).
arcs in a graph with arc weights,
such that the sum of the weights is minimal (22).
More formally, the KCT problem can be defined as follows. Let
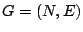 be a graph. A weight
be a graph. A weight 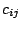 is assigned to each edge
is assigned to each edge
 . A solution
. A solution  is a
is a 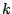 -cardinality tree in
-cardinality tree in 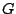 . Let
. Let
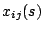 be a binary variable which is 1 if edge
be a binary variable which is 1 if edge
 is
included in
is
included in  , and 0 otherwise. Then, the edge-weighted problem
, and 0 otherwise. Then, the edge-weighted problem
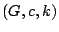 consists of finding a solution
consists of finding a solution  that minimizes
the objective function:
that minimizes
the objective function:
- Transformation of units:
- If the
weight of all edges is multiplied by a constant
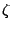 , the resulting
instance
, the resulting
instance 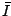 is equivalent to the original
is equivalent to the original 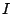 , that is,
, that is,
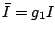 , with
, with 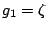 .
Indeed,
.
Indeed,
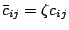 , for all
, for all 
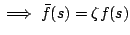 , for all
, for all  .
.
- Reference solution:
- The construction of
the reference solution is typically stochastic.
- Heuristic information:
- The heuristic
information typically used (23) is
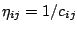 . This meets
Condition 1 with
. This meets
Condition 1 with
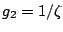 .
.
Therefore, the theorems on the weak invariance of ant system,
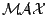 -
-
 ant system, and
ant colony system hold.
ant system, and
ant colony system hold.
- Strongly-invariant heuristic
information:
- Let
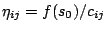 . This meets
Condition 2 with
. This meets
Condition 2 with
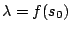 , and
Condition 3.
, and
Condition 3.
Therefore, si AS , si
 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
In the multiple knapsack problem (MKP), a set 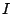 of items and a set
of items and a set
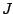 of resources are given. A profit
of resources are given. A profit 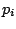 and a requirement
and a requirement
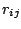 of resource
of resource 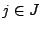 are assigned to each item
are assigned to each item 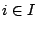 . A
set of constraints is given as a limit
. A
set of constraints is given as a limit 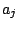 on each resource
on each resource  (24). A solution
(24). A solution  is a subset of items that
meets all the constraints. The goal is to find a solution that
maximizes the total profit. The objective function can be formulate
as:
is a subset of items that
meets all the constraints. The goal is to find a solution that
maximizes the total profit. The objective function can be formulate
as:
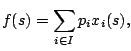 with with 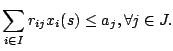 |
|
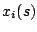 is a binary variable which is 1 if
is a binary variable which is 1 if 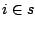 , and 0
otherwise.
, and 0
otherwise.
- Transformation of units:
- If the
profit associated to each item is multiplied by a constant
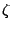 , the resulting
instance
, the resulting
instance 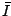 is equivalent to the original
is equivalent to the original 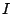 , that is,
, that is,
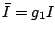 , with
, with 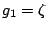 .
.
- Reference solution:
- The construction of
the reference solution is typically stochastic.
- Heuristic information:
- Let
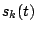 be the partial solution of ant
be the partial solution of ant 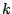 at construction step
at construction step
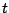 , and
, and
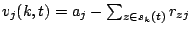 be the
remaining amount of resource
be the
remaining amount of resource  . The tightness of
component
. The tightness of
component 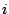 with respect to resource
with respect to resource  is defined as:
is defined as:
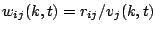 . Finally the average tightness of all
constraints with respect to component
. Finally the average tightness of all
constraints with respect to component 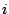 is computed as
is computed as
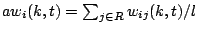 , where
, where 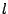 is the number of
resource constraints. Let
is the number of
resource constraints. Let
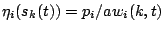 (25). This
definition meets
Condition 1 with
(25). This
definition meets
Condition 1 with 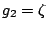 .
.
Therefore, the theorems on the weak invariance of ant system,
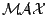 -
-
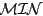 ant system, and
ant colony system hold.
ant system, and
ant colony system hold.
- Strongly-invariant heuristic
information:
- Let
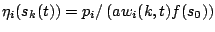 . This meets
Condition 2 with
. This meets
Condition 2 with
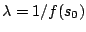 , and
Condition 3.
, and
Condition 3.
Therefore, si AS , si
 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
In the bin packing problem (BPP), a set 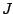 of bins of fixed
capacity
of bins of fixed
capacity 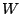 and a set
and a set 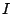 of items are given. A fixed weight
of items are given. A fixed weight 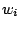 ,
,
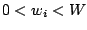 is associated to each item
is associated to each item 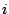 (26). A
solution
(26). A
solution  is an assignment of the items to bins such that the
capacity of the bins is not violated. The goal is to pack the items
in as few bins as possible. More formally, let
is an assignment of the items to bins such that the
capacity of the bins is not violated. The goal is to pack the items
in as few bins as possible. More formally, let 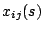 be a
binary variable which is 1 if item
be a
binary variable which is 1 if item 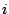 is inserted in bin
is inserted in bin  in
solution
in
solution  , and 0 otherwise. Let
, and 0 otherwise. Let 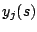 be a binary variable
which is 1 if bin
be a binary variable
which is 1 if bin  is used is solution
is used is solution  , that is, if
, that is, if
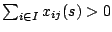 ; and 0 otherwise.
The function to be minimized is:
; and 0 otherwise.
The function to be minimized is:
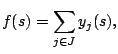 with with 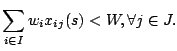 |
|
- Transformation of units:
- If the
capacity of the bins and the weight of all the items are
multiplied by a constant
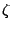 , the resulting
instance
, the resulting
instance 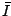 is equivalent to the original
is equivalent to the original 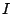 , that is,
, that is,
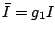 , with
, with 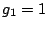 .
.
- Reference solution:
- The construction of
the reference solution is typically done using the best fit decreasing
heuristic.
In this approach, first the items are ordered by decreasing weight. Then,
each of them is assigned to the bin which will have the least
amount of space left, after accommodating the item.
As it can be seen, the selection criterion is invariant to
transformation of units.
- Heuristic information:
- The heuristic information
is typically defined as
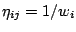 (27). This meets
Condition 1 with
(27). This meets
Condition 1 with 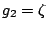 .
.
Therefore, the theorems on the weak invariance of ant system,
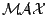 -
-
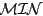 ant system, and
ant colony system hold.
ant system, and
ant colony system hold.
- Strongly-invariant heuristic
information:
- Let
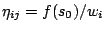 . This meets
Condition 2 with
. This meets
Condition 2 with
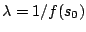 , and
Condition 3.
, and
Condition 3.
Therefore, si AS , si
 AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
AS , and si ACS are indeed strongly invariant
and are functionally equivalent to their original counterparts.
- 1
-
E. L. Lawler, J. K. Lenstra, A. H. G. Rinnooy Kan, and D. B. Shmoys.
The Travelling Salesman Problem.
John Wiley & Sons, Chichester, United Kingdom, 1985.
- 2
-
D. J. Rosenkrantz, R. E. Stearns, and P. M. Lewis II.
An analysis of several heuristics for the traveling salesman problem.
SIAM Journal on Computing, 6 (5): 563-581,
1977.
- 3
-
M. Dorigo and T. Stützle.
Ant Colony Optimization.
MIT Press, Cambridge, MA, USA, 2004.
- 4
-
P. Toth and D. Vigo, editors.
The Vehicle Routing Problem.
SIAM, Philadelphia, PA, USA, 2002.
- 5
-
B. Bullnheimer, R.F. Hartl, and C. Strauss.
An improved ant system for the vehicle routing problem.
Annals of Operations Research, 89: 319-328, 1999.
- 6
-
G. Clarke and J.W. Wright.
Scheduling of vehicles from a central depot to a number of delivery
points.
Operations Research, 12: 568-581, 1964.
- 7
-
M. Reimann, M. Stummer, and K. Doerner.
A saving based ant system for the vehicle routing problem.
In W.B. Langdon, E. Cantú-Paz, K. Mathias, R. Roy, D. Davis,
R. Poli, K. Balakrishnan, V. Honavar, G. Rudolph, J. Wegener, L. Bull, M.A.
Potter, A.C. Schultz, J.F. Miller, E. Burke, and N. Jonoska, editors, Proceedings of the Genetic and Evolutionary Computation Conference, pages
1317-1325, San Francisco, CA, USA, 2002. Morgan Kaufmann Publishers.
- 8
-
L.F. Escudero.
An inexact algorithm for the sequential ordering problem.
European Journal of Operational Research, 37:
232-253, 1988.
- 9
-
L.M. Gambardella and M. Dorigo.
Ant colony system hybridized with a new local search for the
sequential ordering problem.
INFORMS Journal on Computing, 12 (3):
237-255, 2000.
- 10
-
T. Stützle and M. Dorigo.
ACO algorithms for the quadratic assignment problem.
In D. Corne, M. Dorigo, and F. Glover, editors, New Ideas in
Optimization, pages 3-50. McGraw-Hill, New York, NY, USA, 1999.
- 11
-
V. Maniezzo, A. Colorni, and M. Dorigo.
The ant system applied to the quadratic assignment problem.
Technical Report TR/IRIDIA/1994-28, IRIDIA, Université Libre de
Bruxelles, Brussels, Belgium, 1994.
- 12
-
V. Maniezzo and A. Colorni.
The ant system applied to the quadratic assignment problem.
IEEE Transactions on Data and Knowledge Engineering,
11 (5): 769-778, 1999.
- 13
-
H.Lourenço and D. Serra.
Adaptive search heuristics for the generalized assignment problem.
Mathware and Soft Computing, 9: 209-234, 2002.
- 14
-
H.A.J. Crauwels, C.N. Potts, and L.N. Van Wassenhove.
Local search heuristics for the single machine total weighted
tardiness scheduling problem.
INFORMS Journal on Computing, 10 (3):
341-350, 1998.
- 15
-
T.E. Morton, R.M. Rachamadugu, and A.Vepsalainen.
Accurate myopic heuristis for tardiness scheduling.
Technical Report 36-83-84, Carnegie Mellon, Pittsburgh, PA, USA,
1984.
- 16
-
M. den Besten, T. Stützle, and M. Dorigo.
Ant colony optimization for the total weighted tardiness problem.
In M. Schoenauer, K. Deb, G. Rudolf, X. Yao, E. Lutton, J.J. Merelo,
and H.-P. Schwefel, editors, Parallel Problem Solving from Nature, 6th
International Conference, PPSN VI, pages 1111-1118, Berlin, Germany, 2000.
Springer Verlag.
- 17
-
L. Chung-Yee and L. Lei.
Scheduling: theory and applications.
Baltzer Science Publishers, Amsterdam, The Netherlands, 1997.
- 18
-
T. Stützle.
An ant approach to the flow shop problem.
In EUFIT'98: The 6th European Congress on Intelligent Techniques
and Soft Computing, Abstract Booklet with CD Rom, pages 1560-1564, Aachen,
Germany, 1998. Verlag Mainz.
- 19
-
A. Caprara, P. Toth, and M. Fischetti.
Algorithms for the set covering problme.
Annals of Operations Research, 89: 353-371, 2000.
- 20
-
G. Leguizamón and Z. Michalewicz.
Ant system for subset problems.
Unpublished, 2000.
- 21
-
R. Hadji, M. Rahoual, E. Talbi, and V. Bachelet.
Ant colony for the set covering problem.
In M. Dorigo, M. Middendorf, and T. Stützle, editors, Proceedings of ANTS 2000--From Ant Colonies to Artificial Ants: 2nd
International Workshop on Ant Algorithms, pages 63-66, Berlin, Germany,
2000. Springer Verlag.
- 22
-
H.W. Hamacher, K. Jørnsten, and F. Maffioli.
Weighted 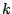 -cardinality trees.
-cardinality trees.
Technical Report 23, Dipartimento di Elettronica, Politecnico di
Milano, Milano, Italy, 1991.
- 23
-
C. Blum and M.J. Blesa.
New metaheuristic approaches for the edge-weighted 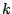 -cardinality
tree problem.
-cardinality
tree problem.
Computers & Operations Research, 32 (6):
1355-1377, 2005.
- 24
-
C.E. Ferreira, A. Martin, and R. Weismantel.
Solving multiple knapsac problems by cutting planes.
SIAM Journal on Optimization, 6 (3):
858-877, 1996.
- 25
-
G. Leguizamón and Z. Michalewicz.
A new version of ant system for subset problems.
In P.J. Angeline, Z. Michalewicz, M. Schoenauer, X. Yao, and
A. Zalzala, editors, Congress on Evolutionary Computation (CEC'99),
pages 1459-1464, Piscataway, NJ, USA, 1999. IEEE Press.
- 26
-
E.G. Coffman Jr., M.R. Garey, and D.S. Johnson.
Approximation algorithms for bin-packing: An updated survey.
In G. Ausiello, M. Lucertini, and P. Serafini, editors, Algorithm Design for Computer Systems Design, pages 49-106. Springer
Verlag, Berlin, Germany, 1984.
- 27
-
J. Levine and F. Ducatelle.
Ant colony optimization and local search for bin packing and cutting
stock problems.
Journal of the Operational Research Society, 55
(7): 705-716, 2004.
![]() be a binary variable taking value 1 if edge
be a binary variable taking value 1 if edge
![]() is
included in tour
is
included in tour ![]() , and 0 otherwise. Let
, and 0 otherwise. Let ![]() be the cost
associated to edge
be the cost
associated to edge
![]() . The goal is to find a
tour
. The goal is to find a
tour ![]() such that the function
such that the function
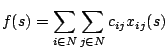
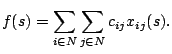

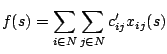
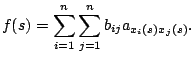
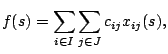 with
with 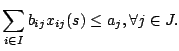
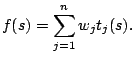
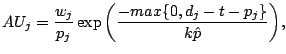 for all
for all 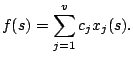
![]() be a graph. A weight
be a graph. A weight ![]() is assigned to each edge
is assigned to each edge
![]() . A solution
. A solution ![]() is a
is a ![]() -cardinality tree in
-cardinality tree in ![]() . Let
. Let
![]() be a binary variable which is 1 if edge
be a binary variable which is 1 if edge
![]() is
included in
is
included in ![]() , and 0 otherwise. Then, the edge-weighted problem
, and 0 otherwise. Then, the edge-weighted problem
![]() consists of finding a solution
consists of finding a solution ![]() that minimizes
the objective function:
that minimizes
the objective function:
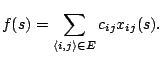
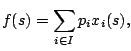 with
with 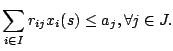
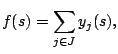 with
with